Regla de la string inversa

Las integrales son una parte importante de la teoría del cálculo. Son muy útiles para calcular áreas y volúmenes de funciones arbitrariamente complejas, que de otro modo serían muy difíciles de calcular y, a menudo, serían malas aproximaciones del área o el volumen encerrado por la función. Las integrales son el reverso de la derivación y por eso se llaman antiderivadas. Hay fórmulas para las integrales de funciones estándar, pero estas fórmulas generalmente no se extienden a los casos en que las funciones se vuelven complejas. Una de esas reglas es la regla de sustitución. Estudiemos esta regla en detalle. 

Regla de la string inversa

La regla de la string para derivadas permite calcular las derivadas de funciones muy complejas que involucran una o más funciones básicas estándar. Para la integración en tales escenarios, existen múltiples trucos o métodos para simplificar los cálculos. Para ciertas clases especiales de funciones, se utiliza la regla de la string inversa . Esta regla también se llama » regla de sustitución» o » regla de sustitución u» . Para usar esta regla, la función debe tener la forma que se muestra a continuación, 

∫f(g(x))g'(x)dx

Observe que en la función de la forma dada, tanto la función g(x) como su derivada g'(x) están presentes. Algunos ejemplos de tales funciones son 

∫cos(x ² ).2xdx

En este caso, g(x) = x ^2, f(x) = cos(x) y g'(x) = 2x. Ahora, para calcular integrales para tales funciones usando la regla de sustitución, se requiere una pequeña modificación. Considere la forma general de tales funciones: 

∫f(g(x))g'(x)dx

Sea u = g(x), diferencie esto de x, 

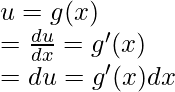
Usando este resultado en la ecuación anterior, 

∫f(u)du

Ahora esta integral se puede calcular y terminar sustituyendo el valor de u en el resultado final. 

∫f(g(x))g'(x)dx = ∫f(u)du, donde u = g(x) 

Cálculo de integrales usando la regla de la string inversa

Es fundamental buscar las posibles funciones y sus derivadas en las funciones integrales dadas. La pregunta natural que viene a la mente es cómo saber cuál es la sustitución correcta. No hay reglas para determinar la sustitución correcta. La intuición para reconocer la sustitución correcta se desarrolla con la práctica. 

Ejemplo 1: Calcular la integral para ∫cos(x ² ).2xdx. 

Responder: 

F(x) = ∫cos(x ² ).2xdx

Busque una función y su derivada en toda la función. En este caso, 

g(x) = x ² y g'(x) = 2x 

Sustituyendo, u = g(x) 

^{⇒ tu =} x2

⇒ du = 2xdx 

F(x) = ∫cos(u)du

⇒F(x) = sen(u) + C

⇒F(x) = sen(x ² ) + C

Ahora considere un tipo diferente de integral: 

Ejemplo 2: Calcular la integral para ∫tan(x)dx. 

Responder: 

F(x) = ∫tan(x)dx

Esto se puede reescribir como, 

Note, aquí g(x) = cos(x) y g'(x) = -sin(x)

Sustituyendo, u = g(x) 

⇒ u = cos(x)

⇒ du = -sen(x)dx 

⇒ -du = sin(x)dx

⇒ 

⇒ F(x) = -ln(u) + C 

⇒ F(x) = -ln(cos(x)) + C

Errores a evitar al usar la regla de la string inversa

Se debe tener cuidado al elegir la función «u» de la función integral original. Si no se elige con cuidado, las integrales pueden volverse demasiado complejas en lugar de simplificarse. Además, en algunos escenarios, las funciones u no son inmediatamente visibles. La siguiente lista presenta algunas cosas que deben tenerse en cuenta al resolver los problemas integrales con la regla de la string inversa. 

1. Para aplicar la regla de la string inversa, la integral debe reescribirse en la forma, 

w(u(x)).u'(x)

Donde la función u es la función interna del factor compuesto. 

2. Al integrar la función compuesta, la función externa solo debe integrarse después de sustituir correctamente la función u y sus derivadas. 

3. A veces, en algunas situaciones, la integral debe dividirse/multiplicarse por algunos factores constantes de variables o la función puede necesitar reorganizarse. Por ejemplo, 

F = ∫tan(x)dx

En este caso, la función u no está completamente clara. Entonces, tan(x) se reescribe en términos de sin(x) y cos(x). 

F = 

Ahora está claro que cos(x) es la función u. 

Problemas de muestra

Pregunta 1: Calcula la integral para ∫cos(e ^x ).e ^x dx. 

Responder: 

F(x) = ∫cos(e ^x ).e ^x dx

Busque una función y su derivada en toda la función. En este caso, 

g(x) = e ^x y g'(x) = e ^x 

Sustituyendo, u = g(x) 

⇒ tu = e ^x

⇒ du = e ^x dx 

F(x) = ∫cos(u)du

⇒F(x) = sen(u) + C

⇒F(x) = sen(e ^x ) + C

Pregunta 2: Calcula la integral para ∫(6x + 4) ⁶ .6dx. 

Responder: 

F(x) = ∫(6x + 4) ⁶ .6dx.

Busque una función y su derivada en toda la función. En este caso, 

g(x) = 6x + 4 y g'(x) = 6 

Sustituyendo, u = g(x) 

⇒ tu = 6x + 4

⇒ du = 6dx 

F(x) = ∫u ⁶ du

⇒F(x) =   + C

⇒F(x) =  + C

Pregunta 3: Calcula la integral para ∫(x ² + 1) ³ .2xdx. 

Responder: 

F(x) = ∫(x ² + 1) ³ .2xdx.

Busque una función, y es derivada de esa función en la función original. En este caso, 

g(x) = x ² + 1 y g'(x) = 2x 

Sustituyendo, u = g(x) 

⇒ tu = x ² + 1

⇒ du = 2xdx 

F(x) = ∫u ³ du

⇒F(x) = 4  + C

⇒F(x) =  + C

Pregunta 4: Calcula la integral para  . 

Responder: 

F(x) = 

Busque una función, y es una derivada de esa función en la función original. En este caso, 

g(x) = x ² + 1 y g'(x) = 2x 

Sustituyendo, u = g(x) 

⇒ tu = x ² + 1

⇒ du = 2xdx 

F(x) = 

⇒F(x) = 

⇒F(x) = 

Pregunta 5: Calcula la integral para  . 

Responder: 

F(x) = 

Busque una función, y es una derivada de esa función en la función original. En este caso, 

g(x) = x + 3 y g'(x) = 1 

Sustituyendo, u = g(x) 

⇒ tu = x + 3

⇒ du = dx 

F(x) = 

⇒F(x) = 

⇒F(x) = ln(x + 3) + C

Pregunta 6: Calcula la integral para 

Responder: 

F(x) = 

Busque una función y su derivada en toda la función. En este caso, 

g(x) = ln(x) y g'(x) = 

Sustituyendo, u = g(x)

⇒ u = ln(x)dx

⇒ du =  

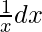
F(x) = ∫u ² du

⇒F(x) =   + C

⇒F(x) =   + C

Pregunta 7: Calcula la integral para ∫sin(1-x)cos(1-x)dx

Responder: 

F(x) = ∫sen(1-x)cos(1-x)dx

Esta función se puede reescribir como, 

F(x) = 

Busque una función y su derivada en toda la función. En este caso, 

g(x) = 2(x -1) y g'(x) = 2

Sustituyendo, u = g(x)

⇒ tu = 2(x – 1)

⇒ du = 2dx 

F(x) = 

⇒F(x) =   + C

⇒F(x) =   + C