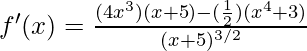En la diferenciación, dos funciones conectadas por algunos operadores también se pueden diferenciar fácilmente según el tipo de operador utilizado. Supongamos que se usa un signo positivo entre dos funciones, las funciones se pueden diferenciar por separado con el signo +ve allí, lo mismo sucede con un signo negativo también. Sin embargo, lo mismo no es posible para la multiplicación o el signo de división. En la multiplicación, cada función se diferencia por separado tomando la otra función como una constante, y si las funciones son de división, la regla se vuelve un poco complicada. Aprendamos sobre esta regla conocida como la regla del cociente en la diferenciación.
¿Qué es la regla del cociente?
Supongamos que se dan dos funciones f(x) y g(x) y ambas funciones son derivables, es decir, existe la derivada de ambas funciones, entonces se usa la regla del cociente para resolver el cociente de las funciones dadas.
La regla del cociente establece que la derivada de la función entera es la derivada del numerador por el denominador menos la derivada del denominador por el numerador entero dividida por el cuadrado del denominador
Es fácil recordar la regla del cociente ya que el numerador es el mismo que el de la regla del producto, solo asegúrate de poner un signo negativo en lugar de uno positivo, además el denominador es el cuadrado de la función del denominador únicamente.
Prueba de la regla del cociente:
Hay varias formas de probar la regla del cociente, una de las formas de probar la regla es usando la definición de derivada estándar y las propiedades límite. La otra forma es simplemente aplicando la regla del producto y ordenando las funciones.
Probemos la regla del cociente por este último método,
para probar ,
Dado , H(x)=f(x)/g(x)
Prueba,
f(x)= H(x)g(x)
Aplicando la regla del producto aquí,
f'(x)=H'(x)g(x)+g'(x)H(x)
Pon el valor de H(x),
Por lo tanto, Probado.
Ejemplos de problemas
Pregunta 1: Diferenciar y= ![]()
Solución:
Tanto las funciones del numerador como del denominador son diferenciables.
Aplicando la regla del cociente,
Pregunta 2: Diferenciar, f(x) = tanx
Solución:
tanx se puede escribir como senx/cosx
Tanto la función del numerador como la del denominador tienen una posible derivada.
Aplicando la regla del cociente,
Pregunta 3: Diferenciar, ![]()
Solución:
Las derivadas tanto del numerador como del denominador están presentes,
Aplicando la regla del cociente,
Pregunta 4: Diferenciar, ![]()
Solución:
Tanto el numerador como el denominador tienen posibles derivadas.
Aplicando la regla del cociente,
Pregunta 5: Diferenciar, f(x)= e x /x 2
Solución:
Tanto el numerador como el denominador tienen posibles derivadas,
Aplicando la regla del cociente,
Pregunta 6: Diferenciar, ![]()
Solución:
Tanto el numerador como el denominador tienen posibles derivadas,
Aplicando la regla del cociente,
Pregunta 7: Diferenciar, f(p)= p+5/p+7
Solución:
Tanto el numerador como el denominador tienen posibles derivadas.
Aplicando la regla del cociente,
Pregunta 8: Diferenciar, f(x)=![]()
Solución:
Tanto el numerador como el denominador tienen posibles derivadas.
Aplicando la regla del cociente,
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
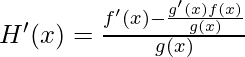
![Rendered by QuickLaTeX.com y'= \frac{[(3x^2-1)(x^2+5)-(x^3-x+2)(2x)]}{[x^2+5]^2}\\=\frac{(3x^4+15x^2-x^2-5)-(2x^4-2x^2+4x)}{[x^2+5]^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-211e91feaa0e15a17e9ee5b4b14a24c4_l3.png)
![Rendered by QuickLaTeX.com y'=\frac{(\frac{1}{2\sqrt{x}}+1)(x+2)-(\sqrt{x}+x)}{[x+2]^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7e384ac11b47cd9267245fba1c022ab6_l3.png)
![Rendered by QuickLaTeX.com y'=\frac{\frac{\sqrt{x}}{2}+\frac{1}{\sqrt{x}}+2-\sqrt{x}}{[x+2]^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-946bd44f2ec3f6f13ef7cf9b04e25a40_l3.png)
![Rendered by QuickLaTeX.com y'=\frac{\frac{-\sqrt{x}}{2}+\frac{1}{\sqrt{x}}+2}{[x+2]^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c44ab6ceaddb629bc5c7f3aab7a77f64_l3.png)