La regresión de Lasso es un algoritmo de clasificación que utiliza la contracción en modelos simples y dispersos (es decir, modelo con menos parámetros). En Shrinkage, los valores de los datos se reducen hacia un punto central como la media. La regresión de Lasso es un algoritmo de regresión regularizado que realiza la regularización L1 que agrega una penalización igual al valor absoluto de la magnitud de los coeficientes.
“LASSO” son las siglas de Least Absolute Shrinkage and Selection Operator . La regresión de lazo es buena para los modelos que muestran altos niveles de multicolinealidad o cuando desea automatizar ciertas partes de la selección del modelo, es decir, la selección de variables o la eliminación de parámetros. Las soluciones de regresión de Lasso son problemas de programación cuadrática que se pueden resolver mejor con software como RStudio , Matlab, etc. Tiene la capacidad de seleccionar predictores.
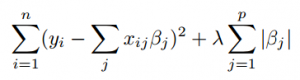
El algoritmo minimiza la suma de cuadrados con restricción. Algunos Beta se reducen a cero, lo que da como resultado un modelo de regresión. Un parámetro de ajuste lambda controla la fuerza de la penalización de regularización L1. lambda es básicamente la cantidad de contracción:
- Cuando lambda = 0, no se elimina ningún parámetro.
- A medida que aumenta lambda , más y más coeficientes se establecen en cero y se eliminan y aumenta el sesgo.
- Cuando lambda = infinito, se eliminan todos los coeficientes.
- A medida que disminuye lambda , aumenta la varianza.
Además, si se incluye una intersección en el modelo, no se modifica. Ahora implementemos la regresión de Lasso en la programación R.
Implementación en R
El conjunto de datos
gran centro comercialEl conjunto de datos consta de 1559 productos en 10 tiendas en diferentes ciudades. Se han definido ciertos atributos de cada producto y tienda. Consta de 12 características, es decir, Item_Identifier (es una identificación de producto única asignada a cada artículo distinto), Item_Weight (incluye el peso del producto), Item_Fat_Content (describe si el producto es bajo en grasa o no), Item_Visibility (menciona el porcentaje de la área de exhibición total de todos los productos en una tienda asignados a un producto en particular), Item_Type (describe la categoría de alimentos a la que pertenece el artículo), Item_MRP (Precio máximo de venta al público (precio de lista) del producto), Outlet_Identifier (ID de tienda único asignado. Consiste en una string alfanumérica de longitud 6), Outlet_Establishment_Year (menciona el año en que se estableció la tienda),
R
# Loading data
train = fread("Train_UWu5bXk.csv")
test = fread("Test_u94Q5KV.csv")
# Structure
str(train)
Producción:
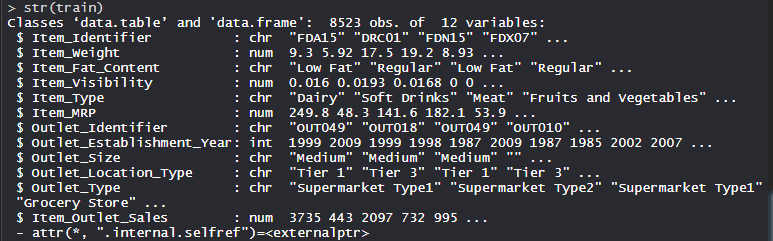
Realización de la regresión de lazo en el conjunto de datos
Usando el algoritmo de regresión de Lasso en el conjunto de datos que incluye 12 funciones con 1559 productos en 10 tiendas en diferentes ciudades.
R
# Installing Packages
install.packages("data.table")
install.packages("dplyr")
install.packages("glmnet")
install.packages("ggplot2")
install.packages("caret")
install.packages("xgboost")
install.packages("e1071")
install.packages("cowplot")
# load packages
library(data.table) # used for reading and manipulation of data
library(dplyr) # used for data manipulation and joining
library(glmnet) # used for regression
library(ggplot2) # used for ploting
library(caret) # used for modeling
library(xgboost) # used for building XGBoost model
library(e1071) # used for skewness
library(cowplot) # used for combining multiple plots
# Loading datasets
train = fread("Train_UWu5bXk.csv")
test = fread("Test_u94Q5KV.csv")
# Setting test dataset
# Combining datasets
# add Item_Outlet_Sales to test data
test[, Item_Outlet_Sales := NA]
combi = rbind(train, test)
# Missing Value Treatment
missing_index = which(is.na(combi$Item_Weight))
for(i in missing_index)
{
item = combi$Item_Identifier[i]
combi$Item_Weight[i] =
mean(combi$Item_Weight[combi$Item_Identifier == item],
na.rm = T)
}
# Replacing 0 in Item_Visibility with mean
zero_index = which(combi$Item_Visibility == 0)
for(i in zero_index)
{
item = combi$Item_Identifier[i]
combi$Item_Visibility[i] =
mean(combi$Item_Visibility[combi$Item_Identifier == item],
na.rm = T)
}
# Label Encoding
# To convert categorical in numerical
combi[, Outlet_Size_num := ifelse(Outlet_Size == "Small", 0,
ifelse(Outlet_Size == "Medium",
1, 2))]
combi[, Outlet_Location_Type_num :=
ifelse(Outlet_Location_Type == "Tier 3", 0,
ifelse(Outlet_Location_Type == "Tier 2", 1, 2))]
combi[, c("Outlet_Size", "Outlet_Location_Type") := NULL]
# One Hot Encoding
# To convert categorical in numerical
ohe_1 = dummyVars("~.", data = combi[, -c("Item_Identifier",
"Outlet_Establishment_Year",
"Item_Type")], fullRank = T)
ohe_df = data.table(predict(ohe_1, combi[, -c("Item_Identifier",
"Outlet_Establishment_Year",
"Item_Type")]))
combi = cbind(combi[, "Item_Identifier"], ohe_df)
# Remove skewness
skewness(combi$Item_Visibility)
skewness(combi$price_per_unit_wt)
# log + 1 to avoid division by zero
combi[, Item_Visibility := log(Item_Visibility + 1)]
# Scaling and Centering data
num_vars = which(sapply(combi, is.numeric)) # index of numeric features
num_vars_names = names(num_vars)
combi_numeric = combi[, setdiff(num_vars_names,
"Item_Outlet_Sales"),
with = F]
prep_num = preProcess(combi_numeric,
method=c("center", "scale"))
combi_numeric_norm = predict(prep_num, combi_numeric)
# removing numeric independent variables
combi[, setdiff(num_vars_names,
"Item_Outlet_Sales") := NULL]
combi = cbind(combi, combi_numeric_norm)
# splitting data back to train and test
train = combi[1:nrow(train)]
test = combi[(nrow(train) + 1):nrow(combi)]
# Removing Item_Outlet_Sales
test[, Item_Outlet_Sales := NULL]
# Model Building :Lasso Regression
set.seed(123)
control = trainControl(method ="cv", number = 5)
Grid_la_reg = expand.grid(alpha = 1,
lambda = seq(0.001, 0.1, by = 0.0002))
# Training lasso regression model
lasso_model = train(x = train[, -c("Item_Identifier",
"Item_Outlet_Sales")],
y = train$Item_Outlet_Sales,
method = "glmnet",
trControl = control,
tuneGrid = Grid_reg
)
lasso_model
# mean validation score
mean(lasso_model$resample$RMSE)
# Plot
plot(lasso_model, main = "Lasso Regression")
Producción:
- Modelo lasso_model:

El modelo de regresión de Lasso utiliza el valor alfa como 1 y el valor lambda como 0,1. Se utilizó RMSE para seleccionar el modelo óptimo utilizando el valor más pequeño.
- Puntuación media de validación:

La puntuación media de validación del modelo es 1128,869.
- Gráfico:

El parámetro de regularización aumenta, RMSE permanece constante.