requisitos previos
Resumiremos brevemente la regresión lineal antes de implementarla usando Tensorflow. Dado que no entraremos en los detalles de Regresión lineal o Tensorflow, lea los siguientes artículos para obtener más detalles:
- Regresión lineal (Implementación de Python)
- Introducción a TensorFlow
- Introducción a Tensor con Tensorflow
Breve resumen de la regresión lineal
La regresión lineal es un método estadístico muy común que nos permite aprender una función o relación a partir de un conjunto dado de datos continuos. Por ejemplo, se nos dan algunos puntos de datos de xy correspondientes yy necesitamos aprender la relación entre ellos que se llama hipótesis .
En el caso de la regresión Lineal, la hipótesis es una línea recta, es decir, ![]()
donde whay un vector llamado Pesos y bhay un escalar llamado Sesgo . Los pesos y sesgos se denominan parámetros del modelo.
Todo lo que necesitamos hacer es estimar el valor de w y b a partir del conjunto de datos dado, de modo que la hipótesis resultante produzca el menor costo Jque se define por la siguiente función de costo,![]()
donde mes el número de puntos de datos en el conjunto de datos dado. Esta función de costo también se llama Error cuadrático medio .
Para encontrar el valor optimizado de los parámetros para los cuales Jes mínimo, usaremos un algoritmo optimizador de uso común llamado Gradient Descent . El siguiente es el pseudocódigo para Gradient Descent:
Repeat untill Convergence {
w = w - α * δJ/δw
b = b - α * δJ/δb
}
donde αes un hiperparámetro llamado Tasa de aprendizaje .
tensorflow
Tensorflow es una biblioteca de computación de código abierto creada por Google. Es una opción popular para crear aplicaciones que requieren cálculos numéricos de alto nivel y/o necesitan utilizar unidades de procesamiento de gráficos para fines de cálculo. Estas son las principales razones por las que Tensorflow es una de las opciones más populares para aplicaciones de Machine Learning, especialmente Deep Learning. También tiene API como Estimator que proporciona un alto nivel de abstracción al crear aplicaciones de aprendizaje automático. En este artículo, no usaremos ninguna API de alto nivel, sino que construiremos el modelo de regresión lineal usando Tensorflow de bajo nivel en el modo de ejecución perezoso durante el cual Tensorflow crea un gráfico acíclico dirigido.o DAG que realiza un seguimiento de todos los cálculos y luego ejecuta todos los cálculos realizados dentro de una sesión de Tensorflow .
Implementación
Comenzaremos importando las bibliotecas necesarias. Usaremos Numpy junto con Tensorflow para los cálculos y Matplotlib para el trazado.
Python3
import numpy as np import tensorflow as tf import matplotlib.pyplot as plt
Para que los números aleatorios sean predecibles, definiremos semillas fijas tanto para Numpy como para Tensorflow.
Python3
np.random.seed(101) tf.set_random_seed(101)
Ahora, generemos algunos datos aleatorios para entrenar el modelo de regresión lineal.
Python3
# Generating random linear data # There will be 50 data points ranging from 0 to 50 x = np.linspace(0, 50, 50) y = np.linspace(0, 50, 50) # Adding noise to the random linear data x += np.random.uniform(-4, 4, 50) y += np.random.uniform(-4, 4, 50) n = len(x) # Number of data points
Visualicemos los datos de entrenamiento.
Python3
# Plot of Training Data
plt.scatter(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title("Training Data")
plt.show()
Producción:
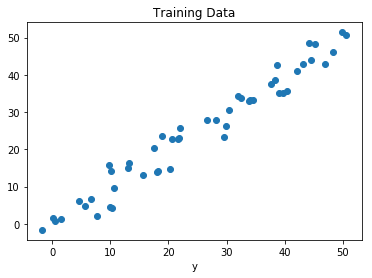
Ahora comenzaremos a crear nuestro modelo definiendo los marcadores X de posición y Y, de modo que podamos alimentar nuestros ejemplos de capacitación Xy Yel optimizador durante el proceso de capacitación.
Python3
X = tf.placeholder("float")
Y = tf.placeholder("float")
Ahora declararemos dos variables Tensorflow entrenables para los pesos y el sesgo y las inicializaremos aleatoriamente usando np.random.randn().
Python3
W = tf.Variable(np.random.randn(), name = "W") b = tf.Variable(np.random.randn(), name = "b")
Ahora definiremos los hiperparámetros del modelo, la tasa de aprendizaje y el número de épocas.
Python3
learning_rate = 0.01 training_epochs = 1000
Ahora, construiremos la Hipótesis, la Función de Costo y el Optimizador. No implementaremos Gradient Descent Optimizer manualmente, ya que está integrado en Tensorflow. Después de eso, inicializaremos las Variables.
Python3
# Hypothesis y_pred = tf.add(tf.multiply(X, W), b) # Mean Squared Error Cost Function cost = tf.reduce_sum(tf.pow(y_pred-Y, 2)) / (2 * n) # Gradient Descent Optimizer optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost) # Global Variables Initializer init = tf.global_variables_initializer()
Ahora comenzaremos el proceso de entrenamiento dentro de una sesión de Tensorflow.
Python3
# Starting the Tensorflow Session
with tf.Session() as sess:
# Initializing the Variables
sess.run(init)
# Iterating through all the epochs
for epoch in range(training_epochs):
# Feeding each data point into the optimizer using Feed Dictionary
for (_x, _y) in zip(x, y):
sess.run(optimizer, feed_dict = {X : _x, Y : _y})
# Displaying the result after every 50 epochs
if (epoch + 1) % 50 == 0:
# Calculating the cost a every epoch
c = sess.run(cost, feed_dict = {X : x, Y : y})
print("Epoch", (epoch + 1), ": cost =", c, "W =", sess.run(W), "b =", sess.run(b))
# Storing necessary values to be used outside the Session
training_cost = sess.run(cost, feed_dict ={X: x, Y: y})
weight = sess.run(W)
bias = sess.run(b)
Producción:
Epoch: 50 cost = 5.8868036 W = 0.9951241 b = 1.2381054
Epoch: 100 cost = 5.7912707 W = 0.99812365 b = 1.0914398
Epoch: 150 cost = 5.7119675 W = 1.0008028 b = 0.96044314
Epoch: 200 cost = 5.6459413 W = 1.0031956 b = 0.8434396
Epoch: 250 cost = 5.590799 W = 1.0053328 b = 0.7389357
Epoch: 300 cost = 5.544608 W = 1.007242 b = 0.6455922
Epoch: 350 cost = 5.5057883 W = 1.008947 b = 0.56222
Epoch: 400 cost = 5.473066 W = 1.01047 b = 0.48775345
Epoch: 450 cost = 5.4453845 W = 1.0118302 b = 0.42124167
Epoch: 500 cost = 5.421903 W = 1.0130452 b = 0.36183488
Epoch: 550 cost = 5.4019217 W = 1.0141305 b = 0.30877414
Epoch: 600 cost = 5.3848577 W = 1.0150996 b = 0.26138115
Epoch: 650 cost = 5.370246 W = 1.0159653 b = 0.21905091
Epoch: 700 cost = 5.3576994 W = 1.0167387 b = 0.18124212
Epoch: 750 cost = 5.3468933 W = 1.0174294 b = 0.14747244
Epoch: 800 cost = 5.3375573 W = 1.0180461 b = 0.11730931
Epoch: 850 cost = 5.3294764 W = 1.0185971 b = 0.090368524
Epoch: 900 cost = 5.322459 W = 1.0190892 b = 0.0663058
Epoch: 950 cost = 5.3163586 W = 1.0195289 b = 0.044813324
Epoch: 1000 cost = 5.3110332 W = 1.0199214 b = 0.02561663Ahora veamos el resultado.
Python3
# Calculating the predictions
predictions = weight * x + bias
print("Training cost =", training_cost, "Weight =", weight, "bias =", bias, '\n')
Producción:
Training cost = 5.3110332 Weight = 1.0199214 bias = 0.02561663Tenga en cuenta que, en este caso, tanto el peso como el sesgo son escalares. Esto se debe a que hemos considerado solo una variable dependiente en nuestros datos de entrenamiento. Si tenemos m variables dependientes en nuestro conjunto de datos de entrenamiento, el Peso será un vector m-dimensional mientras que el sesgo será un escalar.
Finalmente, trazaremos nuestro resultado.
Python3
# Plotting the Results
plt.plot(x, y, 'ro', label ='Original data')
plt.plot(x, predictions, label ='Fitted line')
plt.title('Linear Regression Result')
plt.legend()
plt.show()
Producción:

Publicación traducida automáticamente
Artículo escrito por geekyRakshit y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA