Regresión polinomial usando Turicreate

En este artículo, discutiremos la implementación de la regresión polinomial utilizando Turicreate . Regresión polinomial: La regresión polinomial es una forma de análisis de regresión que modela la relación entre una variable dependiente, digamos y , y una variable independiente, digamos x , como un polinomio de grado n . Se expresa como: 

y= b0+b1x1+ b2x12+ b2x13+…… bnx1n

[donde b0, b1, b2, …… bn son coeficientes de regresión]

Así que aprendamos este concepto a través de prácticas.

Paso 1: Importe las bibliotecas importantes y genere un conjunto de datos muy pequeño usando SArray y SFrame en turicreate que usaremos para realizar la regresión polinomial.

# importing required python libraries
import turicreate
import matplotlib.pyplot as plt
import random
  
# Generating datapoints
X = [data for data in range(1, 21)]
Y = [random.randrange(100, 1000, 1) for data in range(20)]
  
# Creating Sarrays from the generated data points
Xs = turicreate.SArray(X, dtype=float)
Ys = turicreate.SArray(Y, dtype=float)
  
print(f"""Xs : {Xs}
\n-------------------------------------------------------------------------------------------\n
Ys : {Ys}""")

Producción:

Paso 2: Trazar los datos generados

# plotting the generated data
plt.scatter(Xs, Ys)
plt.show()

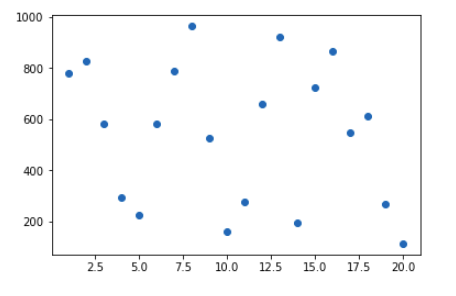
Paso 3: Cree un SFrame que contenga la entrada, sus polinomios_grados y la salida para que se ajuste a nuestro modelo de regresión.

# Creating an Sframe where all the inputs and the polynomial degree and output
def createSframe(inputs, pol_degree):
    datapoints = turicreate.SFrame({'x1': inputs})
    for degree in range(2, pol_degree+1):
        datapoints[f'x{degree}'] = datapoints[f'x{degree-1}']*datapoints['x1']
    return datapoints
  
  
# Creating a SFrame with polynomial degree 20
data_points = createSframe(Xs, 20)
data_points['y'] = Ys
  
# showing the first 10 entries in the SFrame
data_points.head()

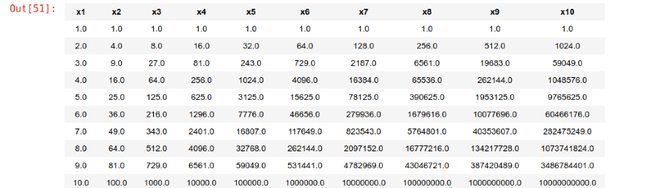
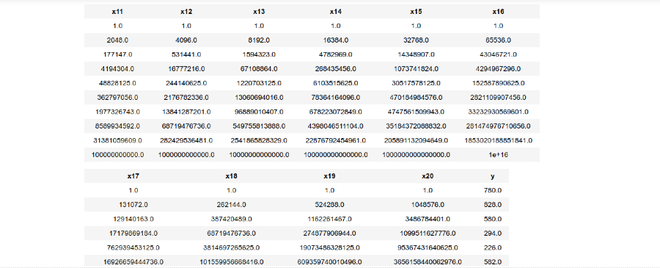
Paso 4: Ajuste de la regresión polinomial al conjunto de datos generado.

# Polynomial Regression
features = [f'x{i}' for i in range(1, 21)]
poly_model = turicreate.linear_regression.create(
    data_points, features=features, target='y')

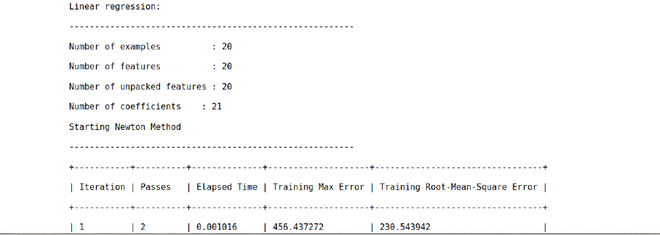
Paso 5: Predecir el resultado utilizando el modelo ajustado y almacenar el resultado en el SFrame.

# predicting the some data
# Generating test datapoints
test_X = [random.randrange(1, 60, 1) for data in range(20)]
test_Xs = turicreate.SArray(X, dtype=float)
test_data = createSframe(test_Xs, 5)
data_points['predicted_y'] = poly_model.predict(test_data)
  
data_points.head()

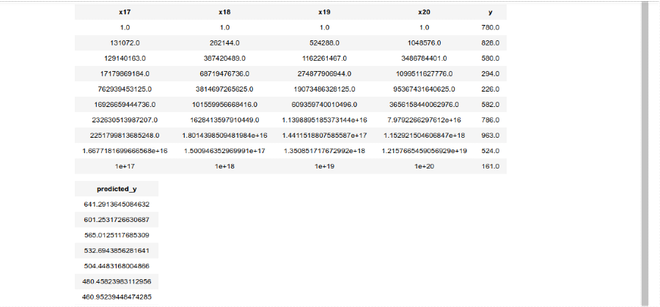
Paso 6: medir la precisión de nuestro resultado previsto

# Measuring the accuracy
# Generating test datapoints
test_X = [random.randrange(1, 60, 1) for data in range(20)]
test_Xs = turicreate.SArray(X, dtype=float)
test_data = createSframe(test_Xs, 20)
poly_model.evaluate(data_points)

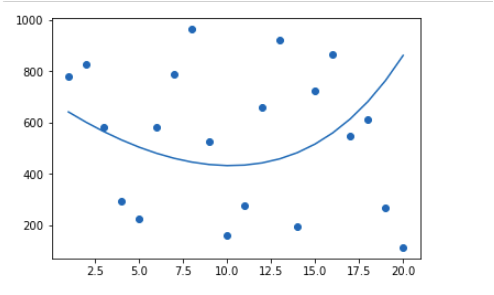
Paso 7: visualización de los resultados de la regresión polinomial utilizando un gráfico de dispersión y un gráfico de líneas de los datos de entrada y el resultado previsto.

plt.scatter(data_points['x1'], data_points['y'])
plt.plot(data_points['x1'], data_points['predicted_y'])
plt.show()