¿Qué es la regresión y la clasificación en el aprendizaje automático?
Los científicos de datos usan muchos tipos diferentes de algoritmos de aprendizaje automático para descubrir patrones en big data que conducen a información útil. A un alto nivel, estos diferentes algoritmos se pueden clasificar en dos grupos según la forma en que «aprenden» sobre los datos para hacer predicciones: aprendizaje supervisado y no supervisado.
Aprendizaje automático supervisado : la mayoría del aprendizaje automático práctico utiliza el aprendizaje supervisado. El aprendizaje supervisado es donde tiene variables de entrada (x) y una variable de salida (Y) y usa un algoritmo para aprender la función de mapeo de la entrada a la salida Y = f(X) . El objetivo es aproximar la función de mapeo tan bien que cuando tenga nuevos datos de entrada (x) pueda predecir las variables de salida (Y) para esos datos.
Las técnicas de algoritmos de aprendizaje automático supervisado incluyen regresión lineal y logística , clasificación multiclase , árboles de decisión y máquinas de vectores de soporte .. El aprendizaje supervisado requiere que los datos utilizados para entrenar el algoritmo ya estén etiquetados con las respuestas correctas. Por ejemplo, un algoritmo de clasificación aprenderá a identificar animales después de ser entrenado en un conjunto de datos de imágenes que están debidamente etiquetadas con la especie del animal y algunas características de identificación.
Los problemas de aprendizaje supervisado se pueden agrupar en problemas de regresión y clasificación . Ambos problemas tienen como objetivo la construcción de un modelo sucinto que pueda predecir el valor del atributo dependiente a partir de las variables de atributo. La diferencia entre las dos tareas es el hecho de que el atributo dependiente es numérico para la regresión y categórico para la clasificación.
Regresión
Un problema de regresión es cuando la variable de salida es un valor real o continuo, como “salario” o “peso”. Se pueden usar muchos modelos diferentes, el más simple es la regresión lineal. Intenta ajustar los datos con el mejor hiperplano que pasa por los puntos.
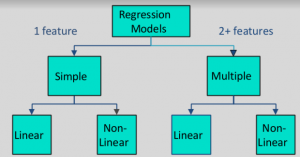
Tipos de modelos de regresión:
Por ejemplo:
¿Cuál de las siguientes es una tarea de regresión?
- Predecir la edad de una persona
- Predecir la nacionalidad de una persona
- Predecir si el precio de las acciones de una empresa aumentará mañana
- ¿Predecir si un documento está relacionado con el avistamiento de ovnis?
Solución: Predecir la edad de una persona (porque es un valor real, predecir la nacionalidad es categórico, si el precio de las acciones aumentará es discreto: respuesta sí/no, predecir si un documento está relacionado con ovnis es nuevamente discreto: respuesta sí/no ).
Tomemos un ejemplo de regresión lineal. Tenemos un conjunto de datos de vivienda y queremos predecir el precio de la casa. A continuación se muestra el código Python para ello.
Python3
# Python code to illustrate
# regression using data set
import matplotlib
matplotlib.use('GTKAgg')
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
import pandas as pd
# Load CSV and columns
df = pd.read_csv("Housing.csv")
Y = df['price']
X = df['lotsize']
X=X.values.reshape(len(X),1)
Y=Y.values.reshape(len(Y),1)
# Split the data into training/testing sets
X_train = X[:-250]
X_test = X[-250:]
# Split the targets into training/testing sets
Y_train = Y[:-250]
Y_test = Y[-250:]
# Plot outputs
plt.scatter(X_test, Y_test, color='black')
plt.title('Test Data')
plt.xlabel('Size')
plt.ylabel('Price')
plt.xticks(())
plt.yticks(())
# Create linear regression object
regr = linear_model.LinearRegression()
# Train the model using the training sets
regr.fit(X_train, Y_train)
# Plot outputs
plt.plot(X_test, regr.predict(X_test), color='red',linewidth=3)
plt.show()
La salida del código anterior será:
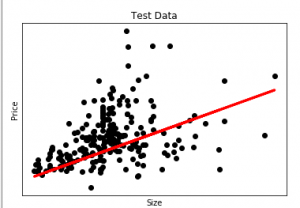
Aquí, en este gráfico, trazamos los datos de prueba. La línea roja indica la línea de mejor ajuste para predecir el precio. Para hacer una predicción individual utilizando el modelo de regresión lineal:
print( str(round(regr.predict(5000))) )
Un problema de clasificación es cuando la variable de salida es una categoría, como «rojo» o «azul» o «enfermedad» y «sin enfermedad». Un modelo de clasificación intenta sacar alguna conclusión de los valores observados. Dadas una o más entradas, un modelo de clasificación intentará predecir el valor de uno o más resultados.
Por ejemplo, al filtrar correos electrónicos como «spam» o «no spam», al buscar datos de transacciones, «fraudulentos» o «autorizados». En resumen, la clasificación predice etiquetas de clase categóricas o clasifica datos (construye un modelo) en función del conjunto de entrenamiento y los valores (etiquetas de clase) en la clasificación de atributos y los usa para clasificar nuevos datos. Hay varios modelos de clasificación. Los modelos de clasificación incluyen regresión logística, árbol de decisión, bosque aleatorio, árbol potenciado por gradiente, perceptrón multicapa, uno contra resto y Naive Bayes.
Por ejemplo:
¿Cuál de los siguientes es(son) problema(s) de clasificación?
- Predecir el género de una persona por su estilo de escritura
- Predicción del precio de la vivienda según el área
- Predecir si el monzón será normal el próximo año
- Prediga el número de copias que se venderá un álbum de música el próximo mes
Solución: Predecir el género de una persona Predecir si el monzón será normal el próximo año. Los otros dos son de regresión.
Ya comentamos la clasificación con algunos ejemplos. Ahora hay un ejemplo de clasificación en el que estamos realizando una clasificación en el conjunto de datos del iris usando RandomForestClassifier en python. Puede descargar el conjunto de datos desde Aquí
Descripción del conjunto de datos
Title: Iris Plants Database
Attribute Information:
1. sepal length in cm
2. sepal width in cm
3. petal length in cm
4. petal width in cm
5. class:
-- Iris Setosa
-- Iris Versicolour
-- Iris Virginica
Missing Attribute Values: None
Class Distribution: 33.3% for each of 3 classes
Python3
# Python code to illustrate
# classification using data set
#Importing the required library
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
from sklearn.metrics import classification_report
#Importing the dataset
dataset = pd.read_csv(
'https://archive.ics.uci.edu/ml/machine-learning-'+
'databases/iris/iris.data',sep= ',', header= None)
data = dataset.iloc[:, :]
#checking for null values
print("Sum of NULL values in each column. ")
print(data.isnull().sum())
#separating the predicting column from the whole dataset
X = data.iloc[:, :-1].values
y = dataset.iloc[:, 4].values
#Encoding the predicting variable
labelencoder_y = LabelEncoder()
y = labelencoder_y.fit_transform(y)
#Splitting the data into test and train dataset
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size = 0.3, random_state = 0)
#Using the random forest classifier for the prediction
classifier=RandomForestClassifier()
classifier=classifier.fit(X_train,y_train)
predicted=classifier.predict(X_test)
#printing the results
print ('Confusion Matrix :')
print(confusion_matrix(y_test, predicted))
print ('Accuracy Score :',accuracy_score(y_test, predicted))
print ('Report : ')
print (classification_report(y_test, predicted))
Producción:
Sum of NULL values in each column.
0 0
1 0
2 0
3 0
4 0
Confusion Matrix :
[[16 0 0]
[ 0 17 1]
[ 0 0 11]]
Accuracy Score : 97.7
Report :
precision recall f1-score support
0 1.00 1.00 1.00 16
1 1.00 0.94 0.97 18
2 0.92 1.00 0.96 11
avg/total 0.98 0.98 0.98 45
Referencias:
- https://machinelearningmastery.com/logistic-regression-for-machine-learning/
- https://machinelearningmastery.com/linear-regression-for-machine-learning/
Publicación traducida automáticamente
Artículo escrito por Sagar Shukla y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
