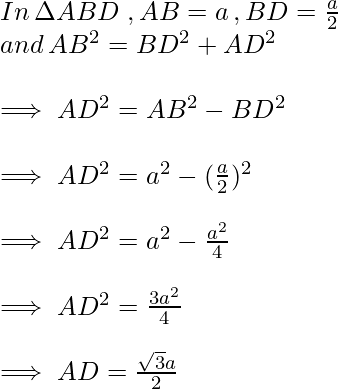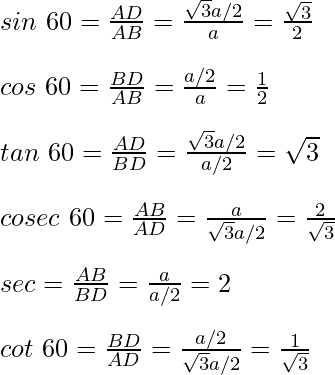La trigonometría tiene que ver con los triángulos o, para ser más precisos, la relación entre los ángulos y los lados de un triángulo (triángulo rectángulo). En este artículo, discutiremos la razón de los lados de un triángulo rectángulo con respecto a su ángulo agudo llamado razones trigonométricas del ángulo y encontraremos las razones trigonométricas de ángulos específicos: 0°, 30°, 45°, 60° y 90°.
Considere el siguiente triángulo,

El lado BA es opuesto al ángulo ∠BCA por lo que llamamos BA el lado opuesto a ∠C y AC es la hipotenusa; el otro lado BC es el lado adyacente a ∠C.
Relaciones trigonométricas del ángulo C
Seno: El seno de ∠C es la razón del lado opuesto a C (BA) a la hipotenusa (AC).
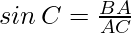
Coseno: El coseno de ∠C es la razón del lado adyacente a C (BC) y la hipotenusa (AC).
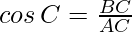
Tangente: La tangente de ∠C es la razón entre el lado opuesto (BA) y el adyacente a C (BC).
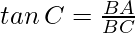
Cosecante: La cosecante de ∠C es el recíproco del sen C por lo tanto es la razón de la hipotenusa (AC) al lado opuesto a C (BA).
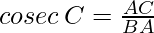
Secante: La secante de ∠C es el recíproco de cos C por lo tanto es la relación de la hipotenusa (AC) al lado adyacente a C (BC).

Cotangente: La cotangente de ∠C es el recíproco de tan C que es la razón del lado adyacente a C (BC) al lado opuesto a C (BA).
Encontrar razones trigonométricas para ángulos 0°, 30°, 45°, 60°, 90°
Considerando la longitud de la hipotenusa AC = a, BC = by, BA = c.
A. Para ángulos de 0° y 90°
Si el ángulo A = 0°, la longitud del lado opuesto sería cero y la hipotenusa = lado adyacente, y si A = 90°, la hipotenusa = lado opuesto. Entonces, con la ayuda de las fórmulas anteriores para las razones trigonométricas obtenemos:
si A = 0°
si A = 90°
Aquí, algunas de las razones trigonométricas resultan como no definidas , ya que en el ángulo particular se divide por 0, que no está definido.
B. Para ángulos de 30° y 60°
Considere un triángulo equilátero ABC. Dado que cada ángulo en un triángulo equilátero es de 60°, por lo tanto,
∠A = ∠B = ∠C = 60°.

∆ABD es un triángulo rectángulo, rectángulo en D con ∠BAD = 30° y ∠ABD = 60°,
Aquí ∆ADB y ∆ADC son similares ya que son partes correspondientes de triángulos congruentes (CPCT) .
Ahora que conocemos los valores de AB, BD y AD, entonces las razones trigonométricas para el ángulo de 30° son,
Para ángulo 60°
C. Para ángulo 45°
En un triángulo rectángulo, si un ángulo mide 45°, entonces el otro ángulo también mide 45°, lo que lo convierte en un triángulo rectángulo isósceles.

Si la longitud del lado BC = a entonces la longitud de AB = a y la longitud de AC(hipotenusa) es a√2 usando el Teorema de Pitágoras , entonces
Todos los valores
| ∠A | 0° | 30° | 45° | 60° | 90° |
| pecado A | 0 | 1/2 | 1/√2 | √3/2 | 1 |
| porque A | 1 | √3/2 | 1/√2 | 1/2 | 0 |
| bronceado A | 0 | 1/√3 | 1 | √3 | No definida |
| cosec A | No definida | 2 | √2 | 2/√3 | 1 |
| segundo A | 1 | 2/√3 | √2 | 2 | No definida |
| cuna A | No definida | √3 | 1 | 1/√3 | 0 |
Publicación traducida automáticamente
Artículo escrito por somsagar2019 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA