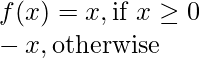Una función en términos muy abstractos se puede considerar como algo que tomará una entrada y producirá una salida. Depende de la función qué tipo de entrada tomará y qué salida dará. Pero, para imaginar, puede pensarse como una máquina o una caja que da una salida para un valor particular de la entrada.

Máquina de función
Entonces, ¿dónde debería uno buscarlo en la vida cotidiana?
Se puede ver en cualquier lugar, por ejemplo, Weatherman toma una lectura del termómetro. El termómetro suele dar una lectura en grados Celsius o Fahrenheit. El meteorólogo luego lo convierte usando alguna fórmula. Se puede pensar en esa fórmula como algo que reside en el cuadro «Máquina de funciones» que se muestra en la figura anterior. Toma la temperatura de entrada en grados Celsius y la convierte a Fahrenheit. Ahora, ¿puede una lectura de grados Celsius darnos dos salidas de temperatura diferentes en Fahrenheit? No. Es por eso que se pone una regla en la máquina de funciones de que no puede dar dos salidas al tomar una entrada.
Veámoslo de una manera formal y matemática.
Funciones y Relación
Producto cartesiano de Conjuntos
Supongamos que A y B son dos conjuntos no vacíos, los conjuntos de todos los pares ordenados (x, y) donde x∈A y y∈B se denominan productos cartesianos de los conjuntos.
UN × segundo = {x, y | x∈A y y∈B}
Pregunta: Encuentra los productos cartesianos del conjunto A ={1,2,3} y B={3,4,5}.
Responder:
Siguiendo la definición anterior, sea el producto cartesiano X,
X = A x B
= {(1,3), (1,4), (1,5), (2,3), (2,4), (2,5), (3,3), (3,4), (3,5)}
Nota: Sea |A| y |B| Sea el número de elementos en el conjunto A y B respectivamente. Sea |X| el número de elementos en el producto cartesiano de los dos conjuntos. Después,
|X| = |A| x |B|
Relación
Una relación del conjunto A al conjunto B es un subconjunto del conjunto de productos cartesianos A x B. El subconjunto se forma describiendo una relación entre el primer elemento y el segundo elemento de elementos en A x B.
Ejemplo: R = {(1,2), (2, -3), (3,5)}
Aquí, en el ejemplo anterior, el conjunto de todos los primeros elementos, es decir, {1,2,5}, se denomina Dominio, mientras que el conjunto de todos los segundos elementos, es decir, {2,-3,5}, se denomina rango de la relación.
Tipos de relación
Hay 8 tipos principales de relaciones que incluyen:
- Relación vacía : no existe relación entre los elementos de un conjunto.
- Relación universal : todos los elementos del conjunto están relacionados entre sí.
- Relación de identidad : en una relación de identidad, cada elemento de un conjunto está relacionado solo consigo mismo.
- Relación inversa: la relación inversa se ve cuando un conjunto tiene elementos que son pares inversos de otro conjunto.
- Relación reflexiva : en una relación reflexiva, cada elemento se asigna a sí mismo.
- Relación simétrica : en una relación asimétrica, si a=b es cierto, entonces b=a también lo es.
- Relación transitiva: para la relación transitiva, si (x, y) ∈ R, (y, z) ∈ R, entonces (x, z) ∈ R.
- Relación de equivalencia : una relación que es simétrica, transitiva y reflexiva al mismo tiempo.
Función
Una función es un tipo especial de relación. Es una relación en la que cada valor de dominio se asigna solo a un valor de rango. Se denota por ƒ:X⇒Y
Lo que esto significa es que es una función de X a Y. Toma la entrada del conjunto X y da el valor único del conjunto Y como salida. «X» se denomina dominio de la función, mientras que «Y» se denomina codominio.

Todas las funciones son relaciones, pero no todas las relaciones son funciones.
Como se describió anteriormente en la introducción, se puede considerar como un bloque/máquina que se ejecuta en alguna fórmula o regla. Toma la entrada y escupe la salida.
Pregunta: ƒ(x) = x 2 . ¿Es una función?
Responder:
Aquí, la función toma un número como entrada. Entonces, su dominio son todos los números reales y en la salida da el cuadrado de ese número como salida. Entonces el codominio serán todos los números positivos.
Ahora, llegando a la pregunta de si esta expresión matemática es una función o no.
De acuerdo con la definición para cada valor de X, debería dar una salida única, pero viceversa no es cierto. Es decir, para diferentes valores de x, puede dar el mismo valor que la salida y aún se considerará como una función.
Por ejemplo: aquí, x = -2 y 2 dan el mismo resultado 4.
Dado que la condición no se viola, se considerará como una función.
Algunos otros ejemplos de funciones:
- x 3 + 1
- sen(x), cos(x)
Tipos de función:
- Función identidad: La función definida por y = f (x) = x para cada x ∈ R.
- Función constante: La función definida por y = f(x) = C, x ∈ R.
- Función polinómica: f(x) = a n x n + a n-1 x n-1 + ….. + a 0
- Función racional: Son funciones de la forma p(x)/q(x).
¿Qué hace que una relación sea una función?
Una relación en la que un elemento se asigna solo a un valor de rango se llama función. Para determinar si una relación es una función, solo debemos asegurarnos de que ningún elemento tenga dos valores de rango correspondientes.
Pregunta 1: En la siguiente tabla se da una relación, averigüe si esta relación es una función o no.
| X | Y |
| 2 | 1 |
| 3 | 6 |
| 2 | 3 |
| 5 | 8 |
Responder:
En esta tabla, cuando x = 2, tenemos dos valores correspondientes de Y. Esto viola la función de propiedad de una entrada-una salida. Así que esto no es una función.
Pregunta 2: En la siguiente tabla se da una relación, averigüe si esta relación es una función o no.
| X | Y |
| 2 | 1 |
| 3 | 4 |
| 5 | 6 |
| 7 | 8 |
Responder:
En la relación anterior, cada entrada tiene solo un valor de rango correspondiente. Entonces, esta relación es una función.
Gráficas de las Funciones
Todas las funciones se pueden trazar en un gráfico, con valores de entrada en el eje x y sus salidas en el eje y. Por ejemplo:
Digamos f(x) = x, donde x puede ser cualquier número real. La gráfica de esta función se verá similar a la gráfica de y = x.

f(x) = x
¿Cómo reconocemos una función a partir de su gráfica?
De la condición que se describió anteriormente, se concluye que no puede haber dos valores de la función en un solo valor de x.
Entonces, veamos algunos ejemplos de funciones y no funciones.
Esta es una gráfica de f(x) = √4x

En el gráfico anterior, la línea vertical discontinua representa un solo valor de x y dos valores de y. Eso significa dos valores cuando se le da un solo valor de x. Esto viola una de las propiedades de la función mencionada anteriormente. Entonces, esto no es una función.
Tomemos otro ejemplo,

En este gráfico anterior, no hay ningún valor de ‘x’ que dé dos resultados diferentes. Una línea discontinua vertical no puede cortar el gráfico en dos lugares. Aunque una línea discontinua horizontal corta el gráfico en dos lugares, esto indica que dos entradas se asignan a la misma salida.
Diferencia entre ecuaciones y funciones
Una función es una expresión, una fórmula. Una ecuación es una igualdad entre dos expresiones.
Entonces 8y + 1 es una expresión que podría llamarse f(y). F(y) = 8y +1 es una ecuación, que pasa a definir una función.
x 2 + y 2 = 4 es una ecuación que no define una función única. Su gráfica es un círculo, que no es una función. La gráfica de ecuaciones representa todos aquellos puntos en los que se cumple la igualdad mientras que la gráfica de una función representa los valores que da la función al dar diferentes valores de entrada.
Ejemplos de muestra
Pregunta 1: Halla el rango de la función: ƒ(x) = ![]()
Solución:
Dado que el valor dentro de la raíz no puede ser negativo, x 2 debe ser menor que 16.
Eso significa x ∈ [-4,4]. Este es el dominio de la función.
Para el rango, sea y=
entonces y 2 = 16 – x 2
o x 2 = 16 – y 2
Como x ∈ [– 4, 4]
Así rango de f = [0, 4]
Pregunta 2: Trace la gráfica de la función f(x) = |x|.
Solución:
Se puede notar que en esto, hay múltiples entradas que se asignan al mismo valor de la función. Por ejemplo:- x = -2 y x = 2 ambos dan f(x) = 2.
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA