Los números racionales son los números enteros p y q expresados en forma de p/q donde q>0. Los números racionales pueden ser positivos, negativos o incluso cero. Los números racionales se pueden representar en la recta numérica. El centro de la recta numérica se llama Origen (O). Los números racionales positivos se ilustran en el lado derecho del cero (llamado origen) y los negativos en el lado izquierdo del origen. La representación de los números racionales en la recta numérica depende del tipo de fracción.
fracciones propias
Dada una fracción p/q, una fracción propia tiene p<q, y por lo tanto p/q < 1 siempre. Además, p/q nunca puede ser cero.
Las fracciones propias positivas, por lo tanto, siempre estarán entre 0 y 1 en la recta numérica. Negativo estará en el lado izquierdo del origen, entre 0 y -1.
Ejemplos de fracciones propias en la recta numérica
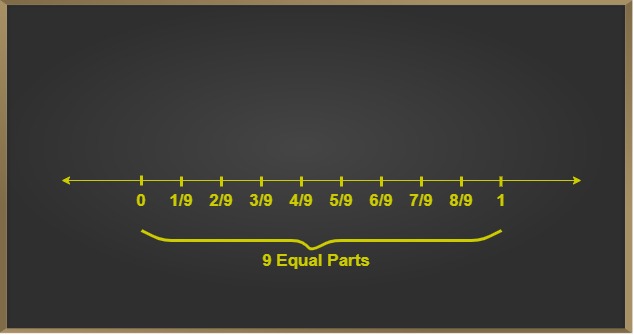
Ejemplo 1: Representación de 5/9 en la recta numérica.
Solución:
- Primero, marcamos el origen y el valor entero 1 en la recta numérica, ya que los números racionales propios se encuentran entre 0 y 1.
- A continuación, dividimos esta región en partes iguales, de modo que estas partes sean iguales al valor del denominador.
- Luego, marcamos la parte con el valor igual al numerador.
Ejemplo 2: Representación de -3/4 en la recta numérica.
Solución:
- Primero, marcamos el origen y el valor entero -1 en la recta numérica, ya que los números racionales propios se encuentran entre 0 y -1.
- A continuación, dividimos esta región en 4 partes iguales.
- Para marcar -3 , mueva tres partes del lado izquierdo del cero.
4

Ejemplo 3: Representación de 1/11 en la recta numérica
Solución:
- Primero, marcamos el origen y el valor entero 1 en la recta numérica, ya que los números racionales propios se encuentran entre 0 y 1.
- A continuación, dividimos esta región en 11 partes iguales.
- Para marcar 1/11, mueva una parte a la derecha del cero.

fracciones impropias
Dada una fracción impropia p/q, el numerador (p) > denominación (q) , tal que la razón p/q>1. Las fracciones impropias se convierten primero en fracciones mixtas, es decir, 11/2 ⇢ 5 1/2, aquí 5 es parte entera, 1/2 es parte fraccionaria.
Ejemplos de fracciones impropias en la recta numérica
Ejemplo 1: Representa 95/4 en una recta numérica.
Solución:
Convirtiendo a una fracción mixta obtenemos, 23 3
4
La fracción mixta se traza en la recta numérica, que se encuentra en el rango de la parte entera y la parte entera +1. Luego, esta región se divide en partes iguales, correspondientes al denominador de la parte fraccionaria y marcando la p -ésima parte (es decir, el numerador). 95 ⇒ 23 3 4 4 Paso 1:

Paso 2:

Paso 3:

Ejemplo 2: Representa -5 en una recta numérica
3
Solución:
Convirtiendo a una fracción mixta obtenemos -5 ⇒ -1 -2
3 3
Aquí -1 es la parte del número entero, – 2 es la parte de la fracción
3
La fracción mixta se traza en la recta numérica, que se encuentra en el rango de la parte entera y parte entera +1. Luego, esta región se divide en partes iguales, correspondientes al denominador de la parte fraccionaria y marcando la p -ésima parte (es decir, el numerador).
-5 ⇒ -1 -2
3 3

En el caso de fracciones negativas, nos movemos hacia el origen.
Ejemplo 3: Representa 5 en una recta numérica.
2
Solución:
Convirtiendo a una fracción mixta obtenemos 5 ⇒ 2 1
2 2
Aquí 1 es la parte del número entero, 1 es la parte de la fracción
2
Las fracciones mixtas se trazan en la recta numérica, que se encuentra en el rango de la parte del número entero y el número entero parte + 1, que es 1 y 2 en este caso. Luego se divide esta región en partes iguales, correspondiendo al denominador de la parte fraccionaria y marcando la parte numeradora. Eso es marcar la 1ra de 2 partes en la recta numérica.
