Encuentre el valor de m y c tal que una línea recta y = mx + c, represente mejor la ecuación de un conjunto dado de puntos (x ![]() , y
, y ![]() ), (x
), (x ![]() , y
, y ![]() ), (x
), (x ![]() , y
, y ![]() ), ……., (x
), ……., (x ![]() , y
, y ![]() ), dado n >=2.
), dado n >=2.
Ejemplos:
Input : n = 5
x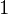 = 1, x
= 1, x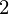 = 2, x
= 2, x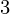 = 3,
x
= 3,
x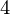 = 4, x
= 4, x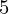 = 5
y
= 5
y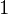 = 14, y
= 14, y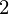 = 27, y
= 27, y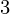 = 40,
y
= 40,
y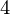 = 55, y
= 55, y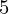 = 68
Output : m = 13.6
c = 0
If we take any pair of number ( x
= 68
Output : m = 13.6
c = 0
If we take any pair of number ( x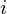 , y
, y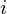 )
from the given data, these value of m and c
should make it best fit into the equation
for a straight line, y = mx + c. Take x
)
from the given data, these value of m and c
should make it best fit into the equation
for a straight line, y = mx + c. Take x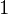 = 1
and y
= 1
and y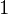 = 14, then using values
of m and c from the output, and putting it
in the following equation,
y = mx + c,
L.H.S.: y = 14, R.H.S: mx + c = 13.6 x 1 + 0 = 13.6
So, they are approximately equal.
Now, take x
= 14, then using values
of m and c from the output, and putting it
in the following equation,
y = mx + c,
L.H.S.: y = 14, R.H.S: mx + c = 13.6 x 1 + 0 = 13.6
So, they are approximately equal.
Now, take x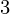 = 3 and y
= 3 and y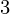 = 40,
L.H.S.: y = 40, R.H.S: mx + c = 13.6 x 3 + 0 = 40.8
So, they are also approximately equal, and so on
for all other values.
Input : n = 6
x
= 40,
L.H.S.: y = 40, R.H.S: mx + c = 13.6 x 3 + 0 = 40.8
So, they are also approximately equal, and so on
for all other values.
Input : n = 6
x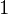 = 1, x
= 1, x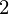 = 2, x
= 2, x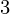 = 3,
x
= 3,
x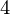 = 4, x
= 4, x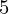 = 5, x
= 5, x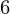 = 6
y
= 6
y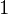 = 1200, y
= 1200, y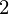 = 900, y
= 900, y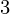 = 600,
y
= 600,
y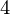 = 200, y
= 200, y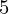 = 110, y
= 110, y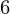 = 50
Output : m = -243.42
c = 1361.97
= 50
Output : m = -243.42
c = 1361.97
Acercarse
Para ajustar mejor un conjunto de puntos en una ecuación de una línea recta, necesitamos encontrar el valor de dos variables, m y c. Ahora, dado que hay 2 variables desconocidas y dependiendo del valor de n, son posibles dos casos:
Caso 1: cuando n = 2: habrá que encontrar dos ecuaciones y dos variables desconocidas, por lo que habrá una solución única.
Caso 2 – Cuando n > 2: En este caso, pueden o no existir valores de m y c, que satisfagan todas las n ecuaciones, pero podemos encontrar los mejores valores posibles de m y c que se ajusten a una línea recta en los puntos dados.
Entonces, si tenemos n pares diferentes de x e y, entonces podemos formar n no. de ecuaciones de ellos para una línea recta, como sigue
f= mx
+ c, f
= mx
+ c, f
= mx
+ c, ......................................, ......................................, f
= mx
+ c, where, f
, is the value obtained by putting x
in equation mx + c.
Entonces, dado que idealmente f ![]() debería ser igual a y
debería ser igual a y ![]() , pero aun así podemos encontrar la f
, pero aun así podemos encontrar la f ![]() más cercana a y
más cercana a y ![]() en todos los casos, si tomamos una nueva cantidad, U = ?(y
en todos los casos, si tomamos una nueva cantidad, U = ?(y ![]() – f
– f ![]() )
) ![]() , y hacemos que esta cantidad sea mínima para todos los valores de i de 1 a n.
, y hacemos que esta cantidad sea mínima para todos los valores de i de 1 a n.
Nota: (y ![]() – f
– f ![]() )
) ![]() se usa en lugar de (y
se usa en lugar de (y ![]() – f
– f ![]() ), ya que queremos considerar ambos casos cuando f
), ya que queremos considerar ambos casos cuando f ![]() o cuando y
o cuando y ![]() es mayor, y queremos que su diferencia sea mínima, por lo que si no elevamos al cuadrado término, entonces las situaciones en las que f
es mayor, y queremos que su diferencia sea mínima, por lo que si no elevamos al cuadrado término, entonces las situaciones en las que f ![]()
es mayor y las situaciones en las que y ![]() es mayor se anularán entre sí hasta cierto punto, y esto no es lo que queremos. Entonces, tenemos que elevar al cuadrado el término.
es mayor se anularán entre sí hasta cierto punto, y esto no es lo que queremos. Entonces, tenemos que elevar al cuadrado el término.
Ahora, para que U sea mínimo, debe satisfacer las siguientes dos ecuaciones:
= 0 and
= 0.
Al resolver las dos ecuaciones anteriores, obtenemos dos ecuaciones, de la siguiente manera:
?y = nc + m?x, and ?xy = c?x + m?x, which can be rearranged as - m = (n * ?xy - ?x?y) / (n * ?x
- (?x)
), and c = (?y - m?x) / n,
Entonces, así es como se obtienen los valores de m y c para ambos casos, y podemos representar un conjunto dado de puntos, por la mejor línea recta posible.
El siguiente código implementa el algoritmo dado anteriormente:
C++
// C++ Program to find m and c for a straight line given,
// x and y
#include <cmath>
#include <iostream>
using namespace std;
// function to calculate m and c that best fit points
// represented by x[] and y[]
void bestApproximate(int x[], int y[], int n)
{
float m, c, sum_x = 0, sum_y = 0, sum_xy = 0, sum_x2 = 0;
for (int i = 0; i < n; i++) {
sum_x += x[i];
sum_y += y[i];
sum_xy += x[i] * y[i];
sum_x2 += pow(x[i], 2);
}
m = (n * sum_xy - sum_x * sum_y) / (n * sum_x2 - pow(sum_x, 2));
c = (sum_y - m * sum_x) / n;
cout << "m =" << m;
cout << "\nc =" << c;
}
// Driver main function
int main()
{
int x[] = { 1, 2, 3, 4, 5 };
int y[] = { 14, 27, 40, 55, 68 };
int n = sizeof(x) / sizeof(x[0]);
bestApproximate(x, y, n);
return 0;
}
C
// C Program to find m and c for a straight line given,
// x and y
#include <stdio.h>
// function to calculate m and c that best fit points
// represented by x[] and y[]
void bestApproximate(int x[], int y[], int n)
{
int i, j;
float m, c, sum_x = 0, sum_y = 0, sum_xy = 0, sum_x2 = 0;
for (i = 0; i < n; i++) {
sum_x += x[i];
sum_y += y[i];
sum_xy += x[i] * y[i];
sum_x2 += (x[i] * x[i]);
}
m = (n * sum_xy - sum_x * sum_y) / (n * sum_x2 - (sum_x * sum_x));
c = (sum_y - m * sum_x) / n;
printf("m =% f", m);
printf("\nc =% f", c);
}
// Driver main function
int main()
{
int x[] = { 1, 2, 3, 4, 5 };
int y[] = { 14, 27, 40, 55, 68 };
int n = sizeof(x) / sizeof(x[0]);
bestApproximate(x, y, n);
return 0;
}
Java
// Java Program to find m and c for a straight line given,
// x and y
import java.io.*;
import static java.lang.Math.pow;
public class A {
// function to calculate m and c that best fit points
// represented by x[] and y[]
static void bestApproximate(int x[], int y[])
{
int n = x.length;
double m, c, sum_x = 0, sum_y = 0,
sum_xy = 0, sum_x2 = 0;
for (int i = 0; i < n; i++) {
sum_x += x[i];
sum_y += y[i];
sum_xy += x[i] * y[i];
sum_x2 += pow(x[i], 2);
}
m = (n * sum_xy - sum_x * sum_y) / (n * sum_x2 - pow(sum_x, 2));
c = (sum_y - m * sum_x) / n;
System.out.println("m = " + m);
System.out.println("c = " + c);
}
// Driver main function
public static void main(String args[])
{
int x[] = { 1, 2, 3, 4, 5 };
int y[] = { 14, 27, 40, 55, 68 };
bestApproximate(x, y);
}
}
Python3
# python Program to find m and c for
# a straight line given, x and y
# function to calculate m and c that
# best fit points represented by x[]
# and y[]
def bestApproximate(x, y, n):
sum_x = 0
sum_y = 0
sum_xy = 0
sum_x2 = 0
for i in range (0, n):
sum_x += x[i]
sum_y += y[i]
sum_xy += x[i] * y[i]
sum_x2 += pow(x[i], 2)
m = (float)((n * sum_xy - sum_x * sum_y)
/ (n * sum_x2 - pow(sum_x, 2)));
c = (float)(sum_y - m * sum_x) / n;
print("m = ", m);
print("c = ", c);
# Driver main function
x = [1, 2, 3, 4, 5 ]
y = [ 14, 27, 40, 55, 68]
n = len(x)
bestApproximate(x, y, n)
# This code is contributed by Sam007.
C#
// C# Program to find m and c for a
// straight line given, x and y
using System;
class GFG {
// function to calculate m and c that
// best fit points represented by x[] and y[]
static void bestApproximate(int[] x, int[] y)
{
int n = x.Length;
double m, c, sum_x = 0, sum_y = 0,
sum_xy = 0, sum_x2 = 0;
for (int i = 0; i < n; i++) {
sum_x += x[i];
sum_y += y[i];
sum_xy += x[i] * y[i];
sum_x2 += Math.Pow(x[i], 2);
}
m = (n * sum_xy - sum_x * sum_y) / (n * sum_x2 - Math.Pow(sum_x, 2));
c = (sum_y - m * sum_x) / n;
Console.WriteLine("m = " + m);
Console.WriteLine("c = " + c);
}
// Driver main function
public static void Main()
{
int[] x = { 1, 2, 3, 4, 5 };
int[] y = { 14, 27, 40, 55, 68 };
// Function calling
bestApproximate(x, y);
}
}
// This code is contributed by Sam007
PHP
<?php
// PHP Program to find m and c
// for a straight line given,
// x and y
// function to calculate m and
// c that best fit points
// represented by x[] and y[]
function bestApproximate($x, $y, $n)
{
$i; $j;
$m; $c;
$sum_x = 0;
$sum_y = 0;
$sum_xy = 0;
$sum_x2 = 0;
for ($i = 0; $i < $n; $i++)
{
$sum_x += $x[$i];
$sum_y += $y[$i];
$sum_xy += $x[$i] * $y[$i];
$sum_x2 += ($x[$i] * $x[$i]);
}
$m = ($n * $sum_xy - $sum_x * $sum_y) /
($n * $sum_x2 - ($sum_x * $sum_x));
$c = ($sum_y - $m * $sum_x) / $n;
echo "m =", $m;
echo "\nc =", $c;
}
// Driver Code
$x =array(1, 2, 3, 4, 5);
$y =array (14, 27, 40, 55, 68);
$n = sizeof($x);
bestApproximate($x, $y, $n);
// This code is contributed by ajit
?>
Javascript
<script>
// Javascript Program to find m and c
// for a straight line given, x and y
// function to calculate m and c that
// best fit points represented by x[] and y[]
function bestApproximate(x, y, n)
{
let m, c, sum_x = 0, sum_y = 0,
sum_xy = 0, sum_x2 = 0;
for(let i = 0; i < n; i++)
{
sum_x += x[i];
sum_y += y[i];
sum_xy += x[i] * y[i];
sum_x2 += Math.pow(x[i], 2);
}
m = (n * sum_xy - sum_x * sum_y) /
(n * sum_x2 - Math.pow(sum_x, 2));
c = (sum_y - m * sum_x) / n;
document.write("m =" + m);
document.write("<br>c =" + c);
}
// Driver code
let x = [ 1, 2, 3, 4, 5 ];
let y = [ 14, 27, 40, 55, 68 ];
let n = x.length;
bestApproximate(x, y, n);
// This code is contributed by subham348
</script>
Producción:
m=13.6 c=0.0
Análisis del código anterior
: Espacio auxiliar: O (1)
Complejidad del tiempo: O (n). Tenemos un ciclo que itera n veces, y cada vez realiza una constante no. de cómputos.
Referencia-
1-Matemáticas de ingeniería superior por BS Grewal.
Este artículo es una contribución de Mrigendra Singh . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo usando contribuya.geeksforgeeks.org o envíe su artículo por correo a contribuya@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA