Modelo booleano:
Es un modelo de recuperación simple basado en la teoría de conjuntos y el álgebra booleana. Las consultas están diseñadas como expresiones booleanas que tienen una semántica precisa. La estrategia de recuperación se basa en un criterio de decisión binario. El modelo booleano considera que los términos del índice están presentes o ausentes en un documento.
Resolución de problemas:
Considere 5 documentos con un vocabulario de 6 términos
- documento 1 = ‘ término1 término3 ‘
- documento 2 = ‘término 2 término4 término6’
- documento 3 = ‘ término1 término2 término3 término4 término5 ‘
- documento 4 = ‘ término1 término3 término6 ‘
- documento 5 = ‘ término3 término4 ‘
Nuestros documentos en modelo booleano
| termino 1 | término 2 | término 3 | término 4 | término 5 | término 6 | |
| documento 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| documento 2 | 0 | 1 | 0 | 1 | 0 | 1 |
| documento 3 | 1 | 1 | 1 | 1 | 1 | 0 |
| documento 4 | 1 | 0 | 1 | 0 | 0 | 1 |
| documento 5 | 0 | 0 | 1 | 1 | 0 | 0 |
Considere la consulta
Encuentre el documento que consiste en term1 y term3 y no term2
term1 ∧ term3 ∧ ¬ term2
| termino 1 | ¬término 2 | término 3 | término 4 | término 5 | término 6 | |
| documento 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| documento 2 | 0 | 0 | 0 | 1 | 0 | 1 |
| documento 3 | 1 | 0 | 1 | 1 | 1 | 0 |
| documento 4 | 1 | 1 | 1 | 0 | 0 | 1 |
| documento 5 | 0 | 1 | 1 | 1 | 0 | 0 |
- documento 1 : 1 ∧ 1∧ 1 = 1
- documento 2 : 0 ∧ 0 ∧ 0 = 0
- documento 3 : 1 ∧ 1 ∧ 0 = 0
- documento 4 : 1 ∧ 1 ∧ 1 = 1
- documento 5 : 0 ∧ 1 ∧ 1 = 0
Según el cálculo anterior , el documento 1 y el documento 4 son relevantes para la consulta dada.
Modelo vectorial:
El método para realizar las operaciones y las fórmulas requeridas para el cálculo están presentes en el documento anterior que es la parte 1. Considere la siguiente colección de documentos.
- documento1 = ‘uno dos’
- documento2 = ‘tres dos cuatro’
- documento3 =’uno dos tres’
- documento4 =’uno dos’
Las fórmulas utilizadas
![]()
![]()
![]()
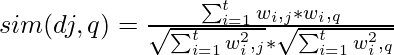
Algunos términos aparecen tres veces, dos veces ya veces sólo una vez en el documento. El número total de documentos N=4. Por lo tanto, los valores IDF de los términos son:
one --> log2(4/3) = 0.4147 two --> log2(4/4) = 0 three --> log2(4/2) = 1 four -->log2(4/1) = 2
Representación en modelo booleano
| una | dos | Tres | cuatro | |
| documento1 | 1 | 1 | 0 | 0 |
| documento2 | 0 | 1 | 1 | 1 |
| documento3 | 1 | 1 | 1 | 0 |
| documento4 | 1 | 1 | 0 | 0 |
Cálculo de la frecuencia del término
one --> 3/4 = 0.75 two --> 4/4 = 1 three --> 2/4 = 0.5 four --> 1/4 = 0.25
Cálculo de pesos ( tf * idf )
weight(one) --> 0.75 * 0.4147 = 0.3110 weight(two) --> 1 * 0 = 0 weight(three) --> 0.5 * 1 = 0.5 weight(four) --> 0.25 * 2 = 0.5
Representación del modelo vectorial en términos de pesos
| una | dos | Tres | cuatro | |
| documento1 | 0.3110 | 0 | 0 | 0 |
| documento2 | 0 | 0 | 0.5 | 0.5 |
| documento3 | 0.3110 | 0 | 0.5 | 0 |
| documento4 | 0.3110 | 0 | 0 | 0 |
CONSULTA: Documento que contiene ‘ uno tres tres ‘
Cálculo de pesos para términos de consulta (frecuencia de términos)
- peso(uno) –> 1/3 = 0.333
- peso(tres) –> 2/3 = 0,667
Representación vectorial
- Documento
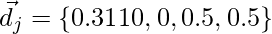
- Consulta
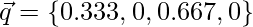
Cálculo de similitud: el

Clasificación de los documentos, (para la clasificación hemos seguido el método de las estadísticas para el caso de asignar la misma clasificación a dos elementos diferentes)
| documento1 | 2do |
| documento2 | 4to |
| documento3 | 1º |
| documento4 | 2do |
Dado que la similitud entre el documento 3 es mayor que las similitudes entre los otros documentos, el tercer documento es más relevante para la consulta.
Publicación traducida automáticamente
Artículo escrito por deviprajwala y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA