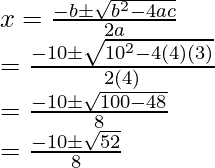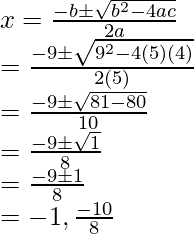Resolver ecuaciones cuadráticas

Las ecuaciones cuadráticas ocurren en casi todas partes en nuestra vida real. Por ejemplo, incluso el problema de diseñar un parque infantil se puede formular como una ecuación cuadrática. Cuando tantas situaciones dan lugar a ecuaciones cuadráticas, despierta un interés genuino en buscar sus soluciones. Digamos que Q(x) = 0 es una ecuación cuadrática. Las soluciones de una ecuación cuadrática representan los puntos donde se cumple esta ecuación que es Q(x) = 0. Las soluciones también se denominan raíces/ceros de la ecuación cuadrática. Veamos algunos enfoques para resolver las ecuaciones cuadráticas.

Ecuación cuadrática

Una ecuación cuadrática es un polinomio de segundo grado. Su forma general está dada por,

hacha ² + bx + c = 0

a, b y c son números reales mientras que a ≠ 0. Su forma es una parábola que se abre hacia arriba o hacia abajo dependiendo del valor de “a”.

Su solución es el punto donde se satisface la ecuación. Hay varios métodos para encontrar una solución a la ecuación cuadrática dada a continuación:

Factorización
Completando el cuadrado
Fórmula cuadrática

Factorización

Tratamos de factorizar la ecuación de manera que obtengamos la ecuación en forma del producto de dos términos. Luego, al igualar estos dos términos a cero, obtenemos las raíces.

Los siguientes pasos deben usarse para encontrar las raíces con factorización:

Todos los términos deben estar en un lado de la ecuación, ya sea LHS o RHS dejando cero en el otro lado.

Factorizar la ecuación

Iguala los factores a cero para encontrar las raíces una por una.

Veamos este método con más detalle usando los siguientes ejemplos:

Pregunta 1: factoriza la siguiente ecuación y encuentra sus raíces: 2x ² – x – 1 = 0

Solución:

2x ² – x – 1 = 0

⇒ 2x ² -2x + x – 1 = 0

⇒ 2x(x – 1) + 1(x – 1) = 0

⇒ (2x + 1) (x – 1) = 0

Para que esta ecuación dos sea cero, uno de estos términos o ambos deben ser cero.

Entonces, podemos encontrar las raíces igualando estos términos con cero.

2x + 1 = 0

x = $-\frac{1}{2}$

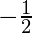
x-1 = 0

⇒ x = 1

Entonces, obtenemos dos raíces en la ecuación.

x = 1 y $-\frac{1}{2}$

Pregunta 2: Factoriza la siguiente ecuación y encuentra sus raíces: x ² + x – 12 = 0

Solución:

x ² + x – 12 = 0

⇒ x2 ⁺ 4x – 3x – 12 = 0

⇒ x(x+4) -3(x+4) = 0

⇒ (x – 3) (x + 4) = 0

Igualando ambos términos con cero.

x – 3 = 0 y x – 4 = 0

x = 3 y 4

Completando el cuadrado

Intentamos traer la ecuación en forma de cuadrados enteros, por ejemplo: (x – a) ² – b ² = 0.

Pasos para encontrar raíces completando el método del cuadrado:

Paso 1: Lleva la ecuación a la forma ax ² + bx = -c.

Paso 2: debemos asegurarnos de que a = 1 (si a≠1, multiplique la ecuación por $\frac{1}{a}$ antes de pasar al siguiente paso).

Paso 3: Usa el valor de b de esta nueva ecuación y $(\frac{b}{2})^2$ en ambos lados de la ecuación para formar un cuadrado perfecto en el lado izquierdo de la ecuación.

Paso 4: Encuentra la raíz cuadrada de ambos lados de la ecuación.

Paso 5: Resuelve el resultado para obtener las raíces.

Veamos algunos ejemplos al respecto,

Pregunta 1: Encuentra las raíces de la siguiente ecuación completando el método del cuadrado.

4x ² + 12x + 9 = 0.

Solución:

4x ² + 12x + 9 = 0

⇒ (2x) ² + 2(3)(2)x + 3 ² = 0

Podemos ver que esta ecuación es un cuadrado perfecto,

⇒ (2x + 3) ² = 0

Para encontrar los ceros en esta ecuación,

2x + 3 = 0

x = $-\frac{3}{2}$

Esta ecuación tiene una raíz repetida, que es x = $-\frac{3}{2}$

La pregunta anterior tenía una ecuación que era un cuadrado perfecto, pero podría no ser el caso siempre. En esos casos, traeremos la ecuación en la forma dada arriba usando los pasos que se mencionan.

Pregunta 2: Encuentra las raíces de la ecuación completando el método del cuadrado.

9x ² + 24x + 3 = 0

Solución:

9x ² + 24x + 3 = 0

Esta ecuación se puede reescribir como,

⇒ 9x ² + 24x + 16 – 13 = 0

⇒ (3x) ² + 24x + 4 ² -13 =0

⇒ (3x + 4) ² -13 = 0

⇒ (3x + 4) ² -(√13) ² = 0

⇒ (3x + 4) ² = (√13) ²

Sacar la raíz cuadrada de ambos lados de la ecuación.

3x + 4 = √13 o 3x + 4 = -√13

Obtenemos nuestras raíces resolviendo estas dos ecuaciones,

3x + 4 = √13

x = $\frac{√13 - 4}{3}$

Similarmente,

3x + 4 = –√13

x = $\frac{-√13 - 4}{3}$

Fórmula cuadrática

Todas las ecuaciones cuadráticas se pueden resolver usando la fórmula cuadrática.

Para una ecuación de la forma,

hacha ² + bx + c = 0,

Donde a, b y c son números reales y a ≠ 0.

Las raíces de esta ecuación están dadas por,

x = $\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

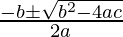
Dado que b ² – 4ac es mayor o igual a cero.

Pregunta 1: Encuentra las raíces de la ecuación usando la fórmula cuadrática,

4x ² + 10x + 3 = 0

Responder:

4x ² + 10x + 3 = 0

Usando la fórmula cuadrática para resolver esto,

a = 4, b = 10 y c = 3

Antes de conectar los valores, necesitamos verificar el discriminador

b2-4ac ^_ _

⇒ 10 ² – 4(4)(3)

⇒ 100 – 48

⇒ 52

Esto es mayor que cero, así que ahora podemos aplicar la fórmula cuadrática.

Reemplazando los valores en la ecuación cuadrática,

$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \\ = \frac{-10 \pm \sqrt{10^2 - 4(4)(3)}}{2(4)} \\ = \frac{-10 \pm \sqrt{100 - 48}}{8} \\ = \frac{-10 \pm \sqrt{52}}{8}$

Pregunta 2: Encuentra las raíces de la ecuación usando la fórmula cuadrática,

5x ² + 9x + 4 = 0

Solución:

5x ² + 9x + 4 = 0

Usando la fórmula cuadrática,

a = 5, b = 9 y c = 4.

Antes de conectar los valores, necesitamos verificar el discriminador

b2-4ac ^_ _

⇒ 9 ² – 4(5)(4)

⇒ 81 – 80

⇒ 1

Esto es mayor que cero, por lo que se puede aplicar la fórmula cuadrática. Introduciendo los valores en la fórmula,

$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \\ = \frac{-9 \pm \sqrt{9^2 - 4(5)(4)}}{2(5)} \\ = \frac{-9 \pm \sqrt{81 - 80}}{10} \\ = \frac{-9 \pm \sqrt{1}}{8} \\ = \frac{-9 \pm 1}{8} \\ = -1, \frac{-10}{8}$

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Ecuación cuadrática

Factorización

Completando el cuadrado

Fórmula cuadrática

Deja una respuesta Cancelar la respuesta