La regresión lineal es un método común para modelar la relación entre una variable dependiente y una o más variables independientes. Los modelos lineales se desarrollan utilizando los parámetros que se estiman a partir de los datos. La regresión lineal es útil en la predicción y el pronóstico donde un modelo predictivo se ajusta a un conjunto de valores de datos observados para determinar la respuesta. Los modelos de regresión lineal a menudo se ajustan utilizando el enfoque de mínimos cuadrados donde el objetivo es minimizar el error.
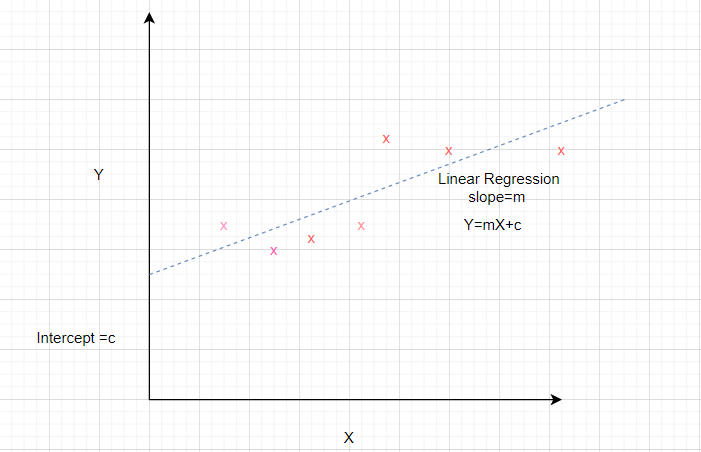
Considere un conjunto de datos donde el atributo independiente está representado por x y el atributo dependiente está representado por y.

Se sabe que la ecuación de una línea recta es y = mx + b donde m es la pendiente y b es la intersección.
Para preparar un modelo de regresión simple del conjunto de datos dado, necesitamos calcular la pendiente y la intersección de la línea que mejor se ajusta a los puntos de datos.
¿Cómo calcular la pendiente y la intersección?
La fórmula matemática para calcular la pendiente y la intersección se dan a continuación.
Slope = Sxy/Sxx where Sxy and Sxx are sample covariance and sample variance respectively. Intercept = ymean – slope* xmean
Usemos estas relaciones para determinar la regresión lineal para el conjunto de datos anterior. Para esto calculamos la media x , la media y , S xy , S xx como se muestra en la tabla.
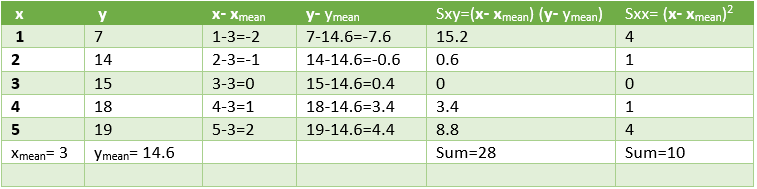
Según las fórmulas anteriores,
Pendiente = 28/10 = 2,8
Intersección = 14,6 – 2,8 * 3 = 6,2
Por lo tanto,
The desired equation of the regression model is y = 2.8 x + 6.2
Usaremos estos valores para predecir los valores de y para los valores dados de x. El rendimiento del modelo puede analizarse calculando el error cuadrático medio y el valor R 2 .
Los cálculos se muestran a continuación.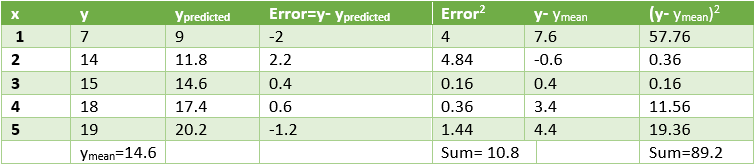
Error cuadrático = 10,8 lo que significa que el error cuadrático medio = 3,28
Coeficiente de determinación (R 2 ) = 1- 10,8 / 89,2 = 0,878
Low value of error and high value of R2 signify that the linear regression fits data well
Veamos la implementación de Python de la regresión lineal para este conjunto de datos.
Código 1: Importar todas las Bibliotecas necesarias.
import numpy as np import matplotlib.pyplot as plt from sklearn.linear_model import LinearRegression from sklearn.metrics import mean_squared_error, r2_score import statsmodels.api as sm
Código 2: Generar los datos. Calcule x mean , y mean , Sxx, Sxy para encontrar el valor de la pendiente y la intersección de la línea de regresión.
x = np.array([1,2,3,4,5])
y = np.array([7,14,15,18,19])
n = np.size(x)
x_mean = np.mean(x)
y_mean = np.mean(y)
x_mean,y_mean
Sxy = np.sum(x*y)- n*x_mean*y_mean
Sxx = np.sum(x*x)-n*x_mean*x_mean
b1 = Sxy/Sxx
b0 = y_mean-b1*x_mean
print('slope b1 is', b1)
print('intercept b0 is', b0)
plt.scatter(x,y)
plt.xlabel('Independent variable X')
plt.ylabel('Dependent variable y')
Producción:
slope b1 is 2.8 intercept b0 is 6.200000000000001
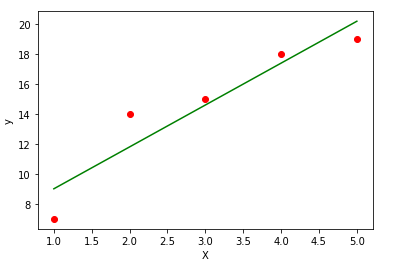
Código 3: Trace los puntos de datos dados y ajuste la línea de regresión.
y_pred = b1 * x + b0
plt.scatter(x, y, color = 'red')
plt.plot(x, y_pred, color = 'green')
plt.xlabel('X')
plt.ylabel('y')
Código 4: Analice el rendimiento del modelo calculando el error cuadrático medio y R 2
error = y - y_pred
se = np.sum(error**2)
print('squared error is', se)
mse = se/n
print('mean squared error is', mse)
rmse = np.sqrt(mse)
print('root mean square error is', rmse)
SSt = np.sum((y - y_mean)**2)
R2 = 1- (se/SSt)
print('R square is', R2)
Producción:
squared error is 10.800000000000004 mean squared error is 2.160000000000001 root mean square error is 1.4696938456699071 R square is 0.8789237668161435
Código 5: use la biblioteca scikit para confirmar los pasos anteriores.
x = x.reshape(-1,1)
regression_model = LinearRegression()
# Fit the data(train the model)
regression_model.fit(x, y)
# Predict
y_predicted = regression_model.predict(x)
# model evaluation
mse=mean_squared_error(y,y_predicted)
rmse = np.sqrt(mean_squared_error(y, y_predicted))
r2 = r2_score(y, y_predicted)
# printing values
print('Slope:' ,regression_model.coef_)
print('Intercept:', regression_model.intercept_)
print('MSE:',mse)
print('Root mean squared error: ', rmse)
print('R2 score: ', r2)
Producción:
Slope: [2.8] Intercept: 6.199999999999999 MSE: 2.160000000000001 Root mean squared error: 1.4696938456699071 R2 score: 0.8789237668161435
Conclusión: este artículo ayuda a comprender las matemáticas detrás de la regresión simple e implementarlas usando Python.