Un rombo es un paralelogramo cuyos cuatro lados tienen todos la misma longitud. También llamado cuadrilátero equilátero. La figura representa un Rombo.
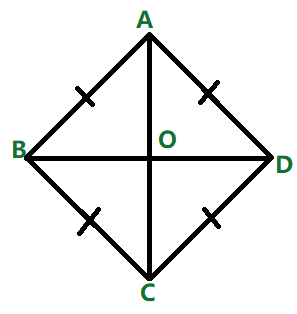
Propiedades
- Todos los lados del rombo son iguales.
- Los lados opuestos de un rombo son paralelos.
- Los ángulos opuestos de un rombo son iguales.
Propiedades de las Diagonales de Rombo
- En un rombo, las diagonales se bisecan en ángulo recto.
- Las diagonales bisecan los ángulos de un rombo.
Probar
1. Si un cuadrilátero es un rombo, entonces las diagonales son bisectrices perpendiculares entre sí.
Primero, probaremos que las diagonales se bisecan entre sí y luego probaremos que las diagonales son perpendiculares entre sí.
(a) Las diagonales se bisecan entre sí

Prueba:
Como el rombo es un paralelogramo, los lados opuestos son paralelos e iguales entre sí.
Así que en el triángulo AOD y COB tenemos
AD = CB (lados opuestos)
∠ADO = ∠CBO (ángulos opuestos)
∠DAO = ∠BCO (ángulos opuestos)
Por lo tanto, ambos triángulos son congruentes.
Por tanto, AO = CO y DO = BO.
Por lo tanto, las diagonales se bisecan entre sí.
(b) Las diagonales son perpendiculares entre sí
Prueba:
Dado que ABCD es un rombo
AB = AD (definición de rombo)
AO = AO (lado común)
BO = OD (las diagonales se bisecan entre sí como se demostró anteriormente)
△AOD ≅ △AOB (Postulado Lado-Lado-Lado)
∠AOD ≅ ∠AOB (Ángulos correspondientes en triángulos congruentes)
También ∠AOD + ∠AOB = 180
Por lo tanto, AC ⊥ DB.
Por lo tanto, las diagonales son la bisectriz perpendicular entre sí.
2. El área del rombo es igual a la mitad del producto de las diagonales.
Prueba:
Dado que ABCD es un rombo, la diagonal AC y BD se cortan en el punto O.

Ahora sabemos que ∠AOD = ∠AOB = ∠COD = ∠BOC = 90 grados.
Por lo tanto, podemos ver que el rombo ABCD se divide igualmente en cuatro partes.
Entonces el área del rombo ABCD = área del triángulo AOD + área del triángulo AOB + área del triángulo BOC+ área del triángulo COD.
1/2 × AO × OD + 1/2 × AO × OB + 1/2 × BO × OC + 1/2 × OD × OC
= 1/2 × AO ( OD + OB ) + 1/2 × OC ( BO + OD )
= 1/2 × ( OD + OB ) × ( AO + OC )
Por tanto, el área del rombo es igual a la mitad del producto de las diagonales.
Ejemplos
Ejemplo 1: ¿Calcular el área de un rombo cuyas diagonales miden 20 cm y 10 cm?
Solución:
Estamos siempre que
d1 = 20 cm
d2 = 10 cm
Área de un rombo, A = (d1 × d2) / 2
= (20 × 10) / 2
= 100cm2
Por lo tanto, el área de un rombo es de 100 cm 2 .
Ejemplo 2: ¿Encontrar el área del rombo que tiene cada lado igual a 25 cm y la longitud de una de sus diagonales es igual a 14 cm?
Solución:
ABCD es un rombo en el que AB = BC = CD = DA = 25 cm
CA = 14 cm
Área del rombo = 1/2 * d 1 * d 2

Por lo tanto, BO = 7 cm
En ∆ AOB,
AB² = AO² + OB²
⇒ 25² = 7² + OB²
⇒ 625 = 49 + OB²
⇒ 576 = OB²
⇒ BO = 24
Por lo tanto, BD = 2 x OB = 2 × 24 = 48 cm
Ahora, el área del rombo = 1/2 × d₁ × d₂ = 1/2 × 14 × 48 = 336 cm²
Por lo tanto, el área del rombo es de 336 cm 2 .
Ejemplo 3: ¿Encontrar la altura del rombo cuya área es de 400 m² y el perímetro es de 160 m?
Solución:
Dado, el perímetro del rombo = 160 m
Entonces, lado del rombo = 160/4 = 40 m
Sabemos que el área de cualquier paralelogramo = b × h
Por lo tanto la altura es:
⇒ 400 = 40 × h
⇒ h = 10m
Por lo tanto, la altura del rombo es de 10 m.
Publicación traducida automáticamente
Artículo escrito por its_just_me y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA