Caminos más cortos desde todos los vértices a un destino

Dado un gráfico dirigido ponderado y un vértice de destino en el gráfico, encuentre la distancia más corta desde todos los vértices hasta el vértice de destino.
Aporte : 
 

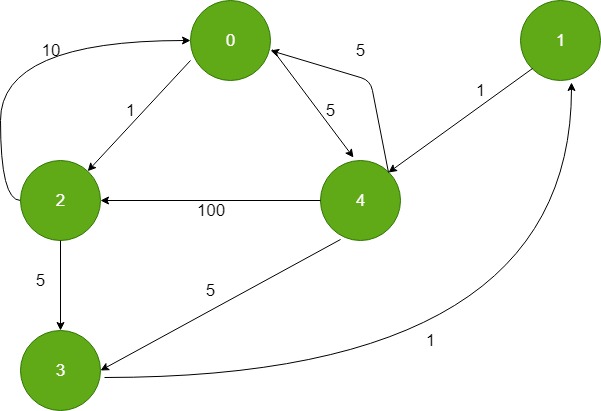
1

Salida: 0 6 10 7 5
Distancia de 0 a 0: 0 
Distancia de 0 a 1: 1+5 = 6 (1->4->0) 
Distancia de 0 a 2: 10 (2->0) 
Distancia de 0 de 3: 1+1+5 = 7 (3->1->4->0) 
Distancia de 0 de 4: 5 (4->0)
 

Enfoque: El problema es similar al problema de Dijkstra. .La idea es utilizar el algoritmo de Dijkstra. Para encontrar la distancia más corta desde todos los vértices hasta un vértice de destino dado, invertimos todos los bordes del gráfico dirigido y usamos el vértice de destino como el vértice de origen en el algoritmo de Dijkstra. Dado que todos los bordes ahora están invertidos, calcular la distancia más corta desde el vértice de destino hasta todos los demás vértices es similar a calcular la distancia más corta desde todos los vértices hasta un vértice de destino dado.
Después de invertir los bordes, el gráfico se ve así: 
 

Ahora calcule la distancia más corta desde el vértice de destino como vértice de origen en el algoritmo de Dijkstra.
A continuación se muestra la implementación del enfoque anterior:
 

// C++ implementation for the above approach
#include <bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
 
// iPair ==>  Integer Pair
typedef pair<int, int> iPair;
 
// This class represents a directed graph using
// adjacency list representation
class Graph {
    int V; // No. of vertices
 
    // In a weighted graph, we need to store vertex
    // and weight pair for every edge
    list<pair<int, int> >* adj;
 
public:
    Graph(int V); // Constructor
 
    // function to add an reverse edge to graph
    void addEdgeRev(int u, int v, int w);
 
    // prints shortest distance from all
    // vertex to the given destination vertex
    void shortestPath(int s);
};
 
// Allocates memory for adjacency list
Graph::Graph(int V)
{
    this->V = V;
    adj = new list<iPair>[V];
}
 
void Graph::addEdgeRev(int u, int v, int w)
{
 
    adj[v].push_back(make_pair(u, w));
}
 
// Prints shortest distance from all vertex to
// the given destination vertex
void Graph::shortestPath(int dest)
{
    // Create a priority queue to store vertices that
    // are being preprocessed. This is weird syntax in C++.
    // Refer below link for details of this syntax
    // https:// www.geeksforgeeks.org/implement-min-heap-using-stl/
    priority_queue<iPair, vector<iPair>, greater<iPair> > pq;
 
    // Create a vector for distances and initialize all
    // distances as infinite (INF)
    vector<int> dist(V, INF);
 
    // Insert destination itself in priority queue and initialize
    // its distance as 0.
    pq.push(make_pair(0, dest));
    dist[dest] = 0;
 
    /* Looping till priority queue becomes empty (or all
      distances are not finalized) */
    while (!pq.empty()) {
 
        // The first vertex in pair is the minimum distance
        // vertex, extract it from priority queue.
        // vertex label is stored in second of pair (it
        // has to be done this way to keep the vertices
        // sorted distance (distance must be first item
        // in pair)
        int u = pq.top().second;
        pq.pop();
 
        // 'i' is used to get all adjacent vertices of a vertex
        list<pair<int, int> >::iterator i;
        for (i = adj[u].begin(); i != adj[u].end(); ++i) {
 
            // Get vertex label and weight of current adjacent
            // of u.
            int v = (*i).first;
            int weight = (*i).second;
 
            // If there is shorted path to v through u.
            if (dist[v] > dist[u] + weight) {
                // Updating distance of v
                dist[v] = dist[u] + weight;
                pq.push(make_pair(dist[v], v));
            }
        }
    }
 
    // Print shortest distances stored in dist[]
    printf("Destination Vertex Distance "
           "from all vertex\n");
    for (int i = 0; i < V; ++i)
        printf("%d \t\t %d\n", i, dist[i]);
}
 
// Driver program to test methods of graph class
int main()
{
    // create the graph given in above figure
    int V = 5;
    Graph g(V);
 
    // adding edges in reverse direction
    g.addEdgeRev(0, 2, 1);
    g.addEdgeRev(0, 4, 5);
    g.addEdgeRev(1, 4, 1);
    g.addEdgeRev(2, 0, 10);
    g.addEdgeRev(2, 3, 5);
    g.addEdgeRev(3, 1, 1);
    g.addEdgeRev(4, 0, 5);
    g.addEdgeRev(4, 2, 100);
    g.addEdgeRev(4, 3, 5);
 
    g.shortestPath(0);
 
    return 0;
}

from queue import PriorityQueue
INF = int(0x3f3f3f3f)
 
# This class represents a directed graph using
# adjacency list representation
class Graph:
    def __init__(self, V: int) -> None:
 
        self.V = V
        # No. of vertices
 
        # In a weighted graph, we need to store vertex
        # and weight pair for every edge
        self.adj = [[] for _ in range(V)]
    def addEdgeRev(self, u: int, v: int, w: int) -> None:
        self.adj[v].append((u, w))
 
    # Prints shortest distance from all vertex to
    # the given destination vertex
    def shortestPath(self, dest: int) -> None:
 
        # Create a priority queue to store vertices that
        # are being preprocessed. This is weird syntax in C++.
        # Refer below link for details of this syntax
        # https:# www.geeksforgeeks.org/implement-min-heap-using-stl/
        pq = PriorityQueue()
 
        # Create a vector for distances and initialize all
        # distances as infinite (INF)
        dist = [INF for _ in range(V)]
 
        # Insert destination itself in priority queue and initialize
        # its distance as 0.
        pq.put((0, dest))
        dist[dest] = 0
 
        # Looping till priority queue becomes empty (or all
        # distances are not finalized) */
        while not pq.empty():
 
            # The first vertex in pair is the minimum distance
            # vertex, extract it from priority queue.
            # vertex label is stored in second of pair (it
            # has to be done this way to keep the vertices
            # sorted distance (distance must be first item
            # in pair)
            u = pq.get()[1]
 
            # 'i' is used to get all adjacent vertices of a vertex
            for i in self.adj[u]:
 
                # Get vertex label and weight of current adjacent
                # of u.
                v = i[0]
                weight = i[1]
 
                # If there is shorted path to v through u.
                if (dist[v] > dist[u] + weight):
                     
                    # Updating distance of v
                    dist[v] = dist[u] + weight
                    pq.put((dist[v], v))
 
        # Print shortest distances stored in dist[]
        print("Destination Vertex Distance from all vertex")
        for i in range(V):
            print("{} \t\t {}".format(i, dist[i]))
 
# Driver code
if __name__ == "__main__":
 
    # create the graph given in above figure
    V = 5
    g = Graph(V)
 
    # adding edges in reverse direction
    g.addEdgeRev(0, 2, 1)
    g.addEdgeRev(0, 4, 5)
    g.addEdgeRev(1, 4, 1)
    g.addEdgeRev(2, 0, 10)
    g.addEdgeRev(2, 3, 5)
    g.addEdgeRev(3, 1, 1)
    g.addEdgeRev(4, 0, 5)
    g.addEdgeRev(4, 2, 100)
    g.addEdgeRev(4, 3, 5)
 
    g.shortestPath(0)
 
# This code is contributed by sanjeev2552

Destination Vertex Distance from all vertex
0                0
1                6
2                10
3                7
4                5