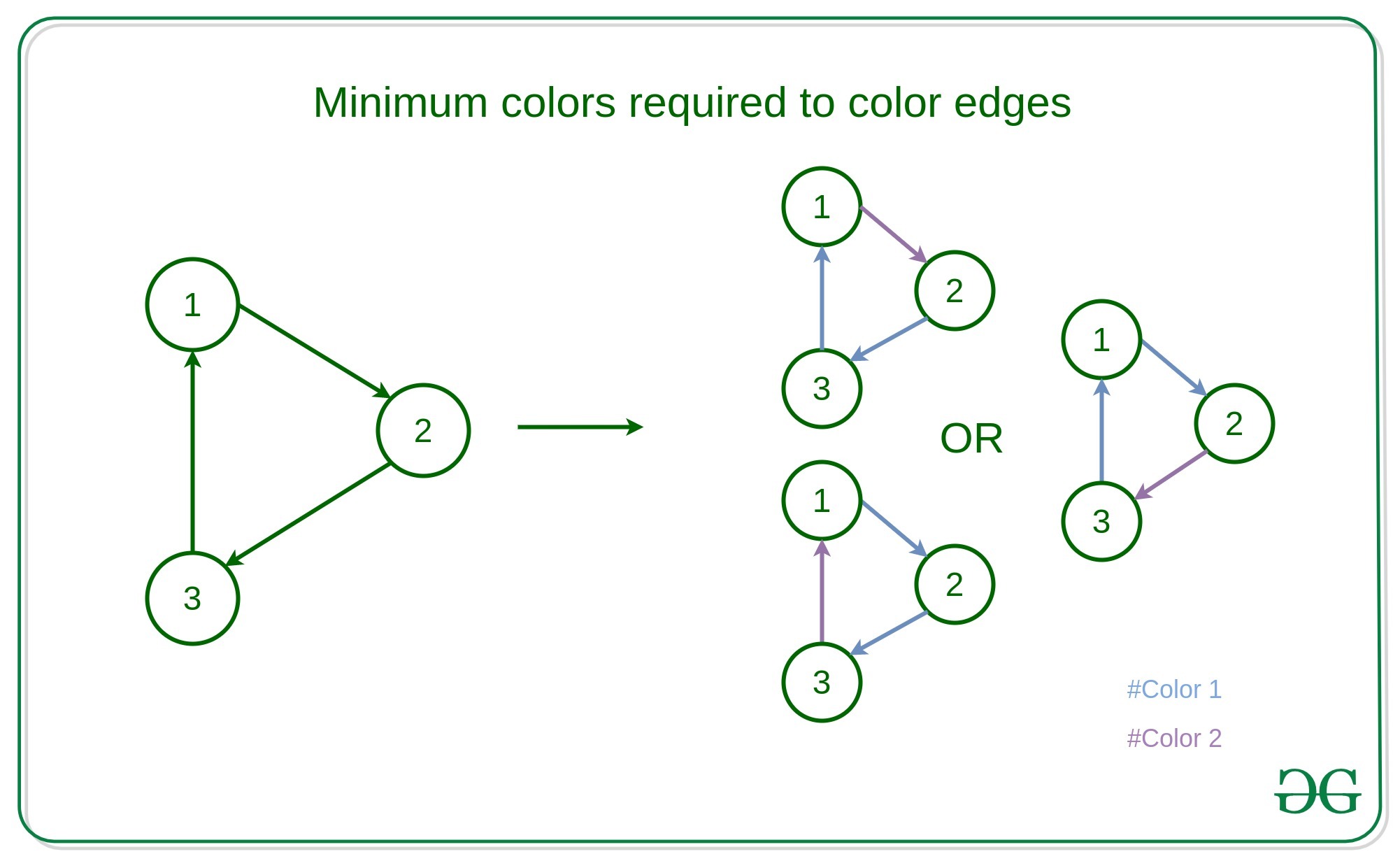
Dado un grafo dirigido con vértices V y aristas E sin bucles automáticos y aristas múltiples, la tarea es encontrar el número mínimo de colores necesarios para que las aristas del mismo color no formen un ciclo y también encontrar los colores para cada arista.
Ejemplos:
Entrada: V = {1, 2, 3}, E = {(1, 2), (2, 3), (3, 1)}
Salida: 2
1 1 2
Explicación:
en el gráfico anterior, forma solo un ciclo,
es decir, los vértices que conectan 1, 2, 3 forman un ciclo.
Luego, los bordes que conectan 1->2 o 2->3 o 3->1 se pueden colorear
con un color diferente . tal que el ciclo de formación de bordes no tiene el mismo color
Entrada: V = {1, 2, 3, 4, 5}, E = {(1, 2), (1, 3), (2, 3), (2 , 4), (3, 4), (4, 5), (5, 3)}
Salida: 2
colores de bordes – 1 1 1 1 1 1 2
Explicación:
En el gráfico anterior, forma solo un ciclo,
que Los vértices que conectan 3, 4, 5 forman un ciclo.
Luego, los bordes que conectan 5->3 o 4->5 o 3->4 se pueden colorear
con un color diferente, de modo que los bordes que forman el ciclo no tienen el mismo color.
Colores finales de los bordes:
{1: 1, 2: 1, 3: 1, 4: 1, 5: 1, 6: 1, 7: 2}
La array anterior indica los pares como: borde: código de color
Enfoque: la idea es encontrar el ciclo en el gráfico, lo que se puede hacer con la ayuda de DFS para el gráfico en el que cuando un Node que ya se visitó se visita nuevamente con un nuevo borde, ese borde se colorea con otro color de lo contrario, si no hay un ciclo, todos los bordes se pueden colorear con un solo color.
Algoritmo:
- Marque todos los bordes con el color 1 y todos los vértices como no visitados.
- Atraviese el gráfico utilizando DFS Traversal para el gráfico y marque los Nodes visitados.
- Cuando un Node que ya se ha visitado, el borde que conecta el vértice se marca para ser coloreado con el color 2.
- Imprime los colores de las aristas cuando se visitan todos los vértices.
Explicación con ejemplo:
ensayo detallado del ejemplo 1
| Vértice actual | Borde actual | Vértices visitados | Colores de los bordes | Comentarios |
|---|---|---|---|---|
| 1 | 1–>2 | {1} | {1: 1, 2: 1, 3: 1} | El Node 1 está marcado como visitado y llamando a DFS para el Node 2 |
| 2 | 2–>3 | {1, 2} | {1: 1, 2: 1, 3: 1} | El Node 2 está marcado como visitado y llamando a DFS para el Node 3 |
| 3 | 3–>1 | {1, 2} | {1: 1, 2: 1, 3: 2} | Como 1 ya está visitado, el color de Edge 3 se cambia a 2 |
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ implementation to find the
// minimum colors required to
// such that edges forming cycle
// don't have same color
#include <bits/stdc++.h>
using namespace std;
const int n = 5, m = 7;
// Variable to store the graph
vector<pair<int, int> > g[m];
// To store that the
// vertex is visited or not
int col[n];
// Boolean Value to store that
// graph contains cycle or not
bool cyc;
// Variable to store the color
// of the edges of the graph
int res[m];
// Function to traverse graph
// using DFS Traversal
void dfs(int v)
{
col[v] = 1;
// Loop to iterate for all
// edges from the source vertex
for (auto p : g[v]) {
int to = p.first, id = p.second;
// If the vertex is not visited
if (col[to] == 0)
{
dfs(to);
res[id] = 1;
}
// Condition to check cross and
// forward edges of the graph
else if (col[to] == 2)
{
res[id] = 1;
}
// Presence of Back Edge
else {
res[id] = 2;
cyc = true;
}
}
col[v] = 2;
}
// Driver Code
int main()
{
g[0].push_back(make_pair(1, 0));
g[0].push_back(make_pair(2, 1));
g[1].push_back(make_pair(2, 2));
g[1].push_back(make_pair(3, 3));
g[2].push_back(make_pair(3, 4));
g[3].push_back(make_pair(4, 5));
g[4].push_back(make_pair(2, 6));
// Loop to run DFS Traversal on
// vertex which is not visited
for (int i = 0; i < n; ++i) {
if (col[i] == 0)
{
dfs(i);
}
}
cout << (cyc ? 2 : 1) << endl;
// Loop to print the
// colors of the edges
for (int i = 0; i < m; ++i) {
cout << res[i] << ' ';
}
return 0;
}
Java
// Java implementation to find the
// minimum colors required to
// such that edges forming cycle
// don't have same color
import java.util.*;
class GFG{
static int n = 5, m = 7;
static class pair
{
int first, second;
public pair(int first, int second)
{
this.first = first;
this.second = second;
}
}
// Variable to store the graph
static Vector<pair > []g = new Vector[m];
// To store that the
// vertex is visited or not
static int []col = new int[n];
// Boolean Value to store that
// graph contains cycle or not
static boolean cyc;
// Variable to store the color
// of the edges of the graph
static int []res = new int[m];
// Function to traverse graph
// using DFS Traversal
static void dfs(int v)
{
col[v] = 1;
// Loop to iterate for all
// edges from the source vertex
for (pair p : g[v]) {
int to = p.first, id = p.second;
// If the vertex is not visited
if (col[to] == 0)
{
dfs(to);
res[id] = 1;
}
// Condition to check cross and
// forward edges of the graph
else if (col[to] == 2)
{
res[id] = 1;
}
// Presence of Back Edge
else {
res[id] = 2;
cyc = true;
}
}
col[v] = 2;
}
// Driver Code
public static void main(String[] args)
{
for(int i= 0; i < m; i++)
g[i] = new Vector<pair>();
g[0].add(new pair(1, 0));
g[0].add(new pair(2, 1));
g[1].add(new pair(2, 2));
g[1].add(new pair(3, 3));
g[2].add(new pair(3, 4));
g[3].add(new pair(4, 5));
g[4].add(new pair(2, 6));
// Loop to run DFS Traversal on
// vertex which is not visited
for (int i = 0; i < n; ++i) {
if (col[i] == 0)
{
dfs(i);
}
}
System.out.print((cyc ? 2 : 1) +"\n");
// Loop to print the
// colors of the edges
for (int i = 0; i < m; ++i) {
System.out.print(res[i] +" ");
}
}
}
// This code is contributed by sapnasingh4991
Python3
# Python3 implementation to find the # minimum colors required to # such that edges forming cycle # don't have same color n = 5 m = 7; # Variable to store the graph g = [[] for i in range(m)] # To store that the # vertex is visited or not col = [0 for i in range(n)]; # Boolean Value to store that # graph contains cycle or not cyc = True # Variable to store the color # of the edges of the graph res = [0 for i in range(m)]; # Function to traverse graph # using DFS Traversal def dfs(v): col[v] = 1; # Loop to iterate for all # edges from the source vertex for p in g[v]: to = p[0] id = p[1]; # If the vertex is not visited if (col[to] == 0): dfs(to); res[id] = 1; # Condition to check cross and # forward edges of the graph elif (col[to] == 2): res[id] = 1; # Presence of Back Edge else: res[id] = 2; cyc = True; col[v] = 2; # Driver Code if __name__=='__main__': g[0].append([1, 0]); g[0].append([2, 1]); g[1].append([2, 2]); g[1].append([3, 3]); g[2].append([3, 4]); g[3].append([4, 5]); g[4].append([2, 6]); # Loop to run DFS Traversal on # vertex which is not visited for i in range(n): if (col[i] == 0): dfs(i); print(2 if cyc else 1) # Loop to print the # colors of the edges for i in range(m): print(res[i], end=' ') # This code is contributed by rutvik_56
C#
// C# implementation to find the
// minimum colors required to
// such that edges forming cycle
// don't have same color
using System;
using System.Collections.Generic;
class GFG{
static int n = 5, m = 7;
class pair
{
public int first, second;
public pair(int first, int second)
{
this.first = first;
this.second = second;
}
}
// Variable to store the graph
static List<pair> []g = new List<pair>[m];
// To store that the
// vertex is visited or not
static int []col = new int[n];
// Boolean Value to store that
// graph contains cycle or not
static bool cyc;
// Variable to store the color
// of the edges of the graph
static int []res = new int[m];
// Function to traverse graph
// using DFS Traversal
static void dfs(int v)
{
col[v] = 1;
// Loop to iterate for all
// edges from the source vertex
foreach (pair p in g[v]) {
int to = p.first, id = p.second;
// If the vertex is not visited
if (col[to] == 0)
{
dfs(to);
res[id] = 1;
}
// Condition to check cross and
// forward edges of the graph
else if (col[to] == 2)
{
res[id] = 1;
}
// Presence of Back Edge
else {
res[id] = 2;
cyc = true;
}
}
col[v] = 2;
}
// Driver Code
public static void Main(String[] args)
{
for(int i= 0; i < m; i++)
g[i] = new List<pair>();
g[0].Add(new pair(1, 0));
g[0].Add(new pair(2, 1));
g[1].Add(new pair(2, 2));
g[1].Add(new pair(3, 3));
g[2].Add(new pair(3, 4));
g[3].Add(new pair(4, 5));
g[4].Add(new pair(2, 6));
// Loop to run DFS Traversal on
// vertex which is not visited
for (int i = 0; i < n; ++i) {
if (col[i] == 0)
{
dfs(i);
}
}
Console.Write((cyc ? 2 : 1) +"\n");
// Loop to print the
// colors of the edges
for (int i = 0; i < m; ++i) {
Console.Write(res[i] +" ");
}
}
}
// This code is contributed by PrinciRaj1992
Javascript
<script>
// C++ implementation to find the
// minimum colors required to
// such that edges forming cycle
// don't have same color
const n = 5, m = 7;
// Variable to store the graph
let g = new Array();
for(let i = 0; i<m; i++){
g.push([])
}
// To store that the
// vertex is visited or not
let col = new Array(n).fill(0);
// Boolean Value to store that
// graph contains cycle or not
let cyc;
// Variable to store the color
// of the edges of the graph
let res = new Array(m);
// Function to traverse graph
// using DFS Traversal
function dfs(v)
{
col[v] = 1;
// Loop to iterate for all
// edges from the source vertex
for (let p of g[v]) {
let to = p[0]
let id = p[1];
// If the vertex is not visited
if (col[to] == 0)
{
dfs(to);
res[id] = 1;
}
// Condition to check cross and
// forward edges of the graph
else if (col[to] == 2)
{
res[id] = 1;
}
// Presence of Back Edge
else {
res[id] = 2;
cyc = true;
}
}
col[v] = 2;
}
// Driver Code
g[0].push([1, 0]);
g[0].push([2, 1]);
g[1].push([2, 2]);
g[1].push([3, 3]);
g[2].push([3, 4]);
g[3].push([4, 5]);
g[4].push([2, 6]);
// Loop to run DFS Traversal on
// vertex which is not visited
for (let i = 0; i < n; ++i) {
if (col[i] == 0)
{
dfs(i);
}
}
document.write((cyc ? 2 : 1) + "<br>");
// Loop to print the
// colors of the edges
for (let i = 0; i < m; ++i) {
document.write(res[i] + ' ');
}
// This code is contributed by _saurabh_jaiswal
</script>
2 1 1 1 1 1 1 2
Análisis de rendimiento:
- Complejidad de tiempo: como en el enfoque anterior, existe un recorrido DFS del gráfico que toma el tiempo O (V + E), donde V denota el número de vértices y E denota el número de aristas. Por lo tanto, la Complejidad del Tiempo será O(V + E) .
- Espacio Auxiliar: O(1).
Publicación traducida automáticamente
Artículo escrito por sharadgoyal y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA