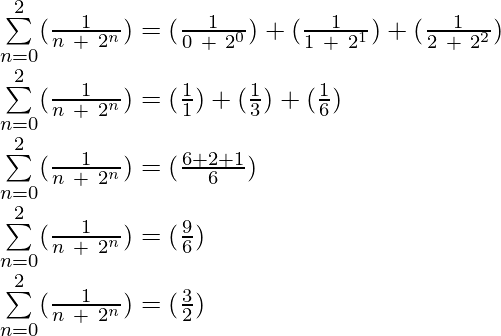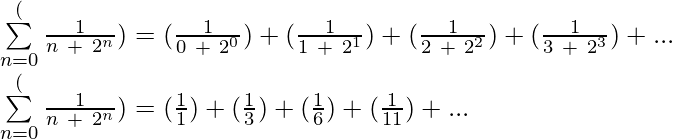En matemáticas, la secuencia es una colección o lista de números que tienen un orden o patrón lógico/secuencial entre ellos. Por ejemplo, 1, 5, 9, 13, … es una secuencia que tiene una diferencia de 4 entre cada término siguiente consecutivo y cada término se puede representar de la forma 1 + 4 * ( n – 1 ) donde n es el enésimo término de la secuencia. La secuencia se puede clasificar en 3 categorías:
- Secuencia aritmética
- Secuencia geométrica
- Secuencia armónica
Secuencia aritmética
La secuencia en la que cada término consecutivo tiene una diferencia común y esta diferencia puede ser positiva, negativa e incluso cero se conoce como secuencia aritmética.
Ejemplo:
1) 0, 2, 4, 6, … en esta secuencia todos y cada uno de los términos consecutivos tienen una diferencia de 2 entre ellos y el término n de la secuencia se puede representar como 2 * ( n – 1 ).
2) 0, 5, 10, 15,… es otro ejemplo de secuencia aritmética con una diferencia de 5 entre cada número consecutivo y el término n de la secuencia se puede representar como 5 * ( n – 1 ).
Secuencia geométrica
La sucesión en la que cada término consecutivo tiene una razón común se conoce como sucesión geométrica.
Ejemplo:
1) 1, 5, 25, 125… en esta secuencia, cada término consecutivo tiene una relación de 5 con el término anterior y el término n de la secuencia se puede representar como 5 (n – 1) .
2) 1, -2, 4, -8, 16, … en esta secuencia, cada término consecutivo tiene una relación de -2 con el término anterior y el término n de la secuencia se puede representar como ( -2 ) ( n – 1 ) .
Secuencia armónica
La secuencia en la que el recíproco de cada término forma una secuencia aritmética se conoce como secuencia armónica.
Ejemplo:
(1/5), (1/10), (1/15), (1/20),… en esta sucesión el recíproco de cada término que es 5, 10, 15, 20,… forma una sucesión aritmética con un diferencia de 5 entre cada término consecutivo.
¿Qué es la notación de suma?
La notación de suma es un método simple para encontrar la suma de una secuencia. La notación de suma también se conoce como notación sigma. Sigma se refiere a la letra griega sigma, Σ. El límite de la secuencia se representa como se muestra en la figura 1, donde el límite inferior es el índice inicial de la secuencia y el límite superior representa el índice final de la secuencia. Como se muestra en la figura 1, el límite inferior es 1 y el límite superior es 4, lo que significa que necesitamos la suma del primer, segundo, tercer y cuarto término, que es (2 * 1) + (2 * 2) + (2 * 3 ) + ( 2 * 4 ) = 2 + 4 + 6 + 8 = 20.
Notación de suma:
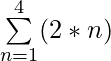
Notación de suma para secuencias aritméticas
La notación sumatoria de sucesiones aritméticas tiene la forma Σ (a + b * n) donde a es el primer término de la sucesión y b es la diferencia común entre dos términos consecutivos cualesquiera de la sucesión y, por lo tanto, el término n de la sucesión sería de la forma (a + (b * n)).
Ejemplo:
Dejemos que la secuencia aritmética sea 0, 2, 4, 6,… así que para hacer la notación de suma necesitamos encontrar los valores de ‘a’ y ‘b’ donde ‘a’ es el primer término que es 0 entonces a = 0 y b es la diferencia común entre 2 términos consecutivos, que en este caso es 2, por lo que b = 2. Por lo tanto, la noción de secuencia de suma sería Σ (0 + (2 * n)) donde el límite inferior es 0 y el límite superior es ∞ como el primer término de la secuencia se da como 0 y el final no está definido.
Notación de suma aritmética:
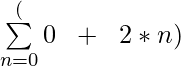
Notación de suma para secuencias geométricas
La notación de sumatoria de sucesiones geométricas tiene la forma Σ (a * b n ) donde a es el primer término de la sucesión y b es la razón común entre dos términos consecutivos cualquiera de la sucesión y, por lo tanto, el enésimo término de la sucesión sería del forma (a * b n ).
Ejemplo:
Dejemos que la secuencia geométrica sea 2, 10, 50, 250, … entonces para hacer la notación de suma necesitamos encontrar los valores de ‘a’ y ‘b’ donde ‘a’ es el primer término que es 2 entonces a = 2 y b es la razón común entre 2 términos consecutivos cualesquiera, que es 5 en este caso, por lo que b = 5. Por lo tanto, la noción de suma de secuencia sería Σ (2 * 5 n ) donde el límite inferior es 0 y el límite superior es ∞ como el el primer término de la secuencia se da como 0 y el final no está definido.
Notación de suma geométrica:
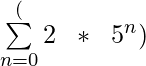
Notación de suma para secuencia armónica
La notación sumatoria de la secuencia armónica tiene la forma Σ ( 1/(a + b*n) ) donde a es el recíproco del primer término de la secuencia y b es la diferencia común entre el recíproco de dos términos consecutivos cualquiera de la secuencia y, por lo tanto, el El término n de la secuencia sería de la forma (1/(a + b * n)).
Ejemplo:
Dejemos que la secuencia aritmética sea 1/2, 1/4, 1/6, … entonces para hacer la notación de suma necesitamos encontrar los valores de ‘a’ y ‘b’ donde ‘a’ es el primer término recíproco que es 2 por lo que a = 2 y b es la diferencia común entre el recíproco de 2 términos consecutivos cualesquiera, que en este caso es 2, por lo que b = 2. Por lo tanto, la noción de sumatoria de secuencia sería Σ (1/( 0 + 2 * n)) donde el límite inferior es 1 y el límite superior es ∞ ya que el primer término de la secuencia se da como 1/2 y el final no está definido.
Notación de suma armónica:
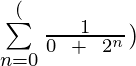
Ejemplos
Ejemplo 1: Encuentra los primeros 4 términos de la sucesión: a n = 2 * x n + 1 y n > 0?
Solución:
Como debemos tener cuidado de reemplazar n (y no x) con los primeros 4 números naturales ya que n no es igual a 0.
un 1 = 2 * x 1 + 1
un 2 = 2 * x 2 + 1
un 3 = 2 * x 3 + 1
un 4 = 2 * x 4 + 1
Ejemplo 2: Encuentra los primeros 6 términos de la sucesión: a n = ![]() y n ≥ 0?
y n ≥ 0?
Solución:
Tenemos que reemplazar n por los primeros 6 mientras números (0, 1, 2, 3, 4, 5).
un 0 =
un 1 =
un 2 =
un 3 =
un 4 =
un 5 =
Ejemplo 3: ¿Evaluar 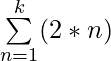 para k = 2 y k = 4?
para k = 2 y k = 4?
Solución:
Para k = 2
= (2 * 1) + (2 * 2) = 2 + 4 = 6
Para k = 4
= (2 * 1) + (2 * 2) + (2 * 3) + (2 * 4) = 2 + 4 + 6 + 8 = 20
Ejemplo 4: Evaluar 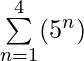 ?
?
Solución:
= (5 1 ) + (5 2 ) + (5 3 ) + (5 4 ) = 5 + 25 + 125 + 625 = 780
Ejemplo 5: Evaluar 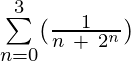 ?
?
Solución:
Ejemplo 6: Escribe en forma desarrollada: 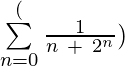 ¿hasta 4 términos?
¿hasta 4 términos?
Solución: