Segmentación de imágenes usando el módulo scikit-image de Python

El proceso de dividir imágenes en varias capas, representadas por una máscara inteligente de píxeles, se conoce como segmentación de imágenes. Implica fusionar, bloquear y separar una imagen de su nivel de integración. Dividir una imagen en una colección de objetos de imagen con propiedades comparables es la primera etapa en el procesamiento de imágenes. Scikit-Image es la herramienta/módulo más popular para el procesamiento de imágenes en Python. 

Instalación

Para instalar este módulo, escriba el siguiente comando en la terminal.

pip install scikit-image

Conversión de formato de imagen

RGB a escala de grises

El módulo rgb2gray del paquete skimage se utiliza para convertir una imagen RGB de 3 canales en una imagen monocromática de un canal. Para aplicar filtros y otras técnicas de procesamiento, la entrada esperada es un vector bidimensional, es decir, una imagen monocromática. 

La función skimage.color.rgb2gray() se usa para convertir una imagen RGB a formato de escala de grises

Sintaxis: skimage.color.rgb2gray(imagen)

Parámetros: imagen: una imagen – formato RGB

Volver : La imagen – Formato en escala de grises

Código:

# Importing Necessary Libraries
from skimage import data
from skimage.color import rgb2gray
import matplotlib.pyplot as plt
 
# Setting the plot size to 15,15
plt.figure(figsize=(15, 15))
 
# Sample Image of scikit-image package
coffee = data.coffee()
plt.subplot(1, 2, 1)
 
# Displaying the sample image
plt.imshow(coffee)
 
# Converting RGB image to Monochrome
gray_coffee = rgb2gray(coffee)
plt.subplot(1, 2, 2)
 
# Displaying the sample image - Monochrome
# Format
plt.imshow(gray_coffee, cmap="gray")

Producción:

Conversión de datos de imagen de 3 canales a datos de imagen de 1 canal

Explicación: Al usar la función rgb2gray(), la imagen RGB de forma de 3 canales (400, 600, 3) se convierte en una imagen de forma monocromática de un solo canal (400, 300). Usaremos imágenes en escala de grises para la implementación adecuada de las funciones de umbral. El promedio de los valores de píxel rojo, verde y azul de cada píxel para obtener el valor de escala de grises es un enfoque simple para convertir una array 3D de imágenes en color en una array 2D en escala de grises. Esto crea una aproximación de gris aceptable al combinar las contribuciones de luminosidad o brillo de cada banda de color.

RGB a HSV

El modelo de color HSV (Tono, Saturación, Valor) reasigna los colores básicos RGB en dimensiones que son más fáciles de comprender para los humanos. El espacio de color RGB describe las proporciones de rojo, verde y azul en un color. En el sistema de color HSV, los colores se definen en términos de matiz, saturación y valor.

La función skimage.color.rgb2hsv() se usa para convertir una imagen RGB a formato HSV

Sintaxis: skimage.color.rgb2hsv(imagen)

Parámetros: imagen: una imagen – formato RGB

Retorno : La imagen – formato HSV

Código:

# Importing Necessary Libraries
from skimage import data
from skimage.color import rgb2hsv
import matplotlib.pyplot as plt
 
# Setting the plot size to 15,15
plt.figure(figsize=(15, 15))
 
# Sample Image of scikit-image package
coffee = data.coffee()
plt.subplot(1, 2, 1)
 
# Displaying the sample image
plt.imshow(coffee)
 
# Converting RGB Image to HSV Image
hsv_coffee = rgb2hsv(coffee)
plt.subplot(1, 2, 2)
 
# Displaying the sample image - HSV Format
hsv_coffee_colorbar = plt.imshow(hsv_coffee)
 
# Adjusting colorbar to fit the size of the image
plt.colorbar(hsv_coffee_colorbar, fraction=0.046, pad=0.04)

Producción:

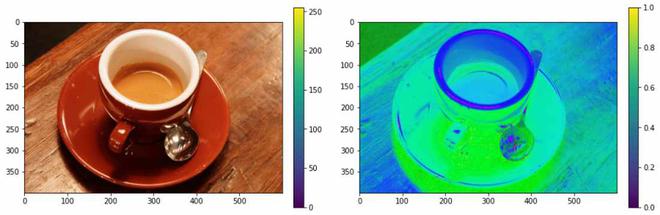
Conversión del formato de color RGB al formato de color HSV

Segmentación Supervisada

Para que este tipo de segmentación proceda, se requiere información externa. Esto incluye cosas como establecer un umbral, convertir formatos y corregir sesgos externos.

Segmentación por umbralización: entrada manual

Se utiliza un valor de píxel externo que oscila entre 0 y 255 para separar la imagen del fondo. Esto da como resultado una imagen modificada que es mayor o menor que el umbral especificado.

# Importing Necessary Libraries
# Displaying the sample image - Monochrome Format
from skimage import data
from skimage import filters
from skimage.color import rgb2gray
import matplotlib.pyplot as plt
 
# Sample Image of scikit-image package
coffee = data.coffee()
gray_coffee = rgb2gray(coffee)
 
# Setting the plot size to 15,15
plt.figure(figsize=(15, 15))
 
for i in range(10):
   
  # Iterating different thresholds
  binarized_gray = (gray_coffee > i*0.1)*1
  plt.subplot(5,2,i+1)
   
  # Rounding of the threshold
  # value to 1 decimal point
  plt.title("Threshold: >"+str(round(i*0.1,1)))
   
  # Displaying the binarized image
  # of various thresholds
  plt.imshow(binarized_gray, cmap = 'gray')
   
plt.tight_layout()

Producción:
 

Explicación: el primer paso en este umbral se implementa al normalizar una imagen de 0 a 255 a 0 a 1. Se fija un valor de umbral y, en la comparación, si se evalúa como verdadero, almacenamos el resultado como 1, de lo contrario, como 0. Esta imagen globalmente binarizada se puede utilizar para detectar bordes y analizar el contraste y la diferencia de color.

Segmentación por Umbral Usando el módulo skimage.filters

La técnica de umbralización de Niblack y Sauvola se ha desarrollado específicamente para mejorar la calidad de las imágenes microscópicas. Es un enfoque de umbralización local que cambia el umbral según la media local y la desviación estándar de cada píxel en una ventana deslizante. La técnica de umbralización de Otsu funciona mediante la iteración de todos los valores de umbral posibles y el cálculo de una medida de dispersión para los puntos de muestra a ambos lados del umbral, es decir, en primer plano o en segundo plano. El objetivo es determinar las extensiones de fondo y primer plano más pequeñas posibles. 

La función skimage.filters.threshold_otsu() se usa para devolver el valor de umbral según el método de Otsu.

Sintaxis: skimage.filters.threshold_otsu(imagen)

Parámetros:

• imagen : Una imagen – Formato monocromático
• nbins : Número de contenedores requeridos para el cálculo del histograma
• hist : Histograma a partir del cual se debe calcular el umbral

Retorno: umbral: mayor intensidad de píxel 

La función skimage.filters.threshold_niblack() es una función de umbral local que devuelve un valor de umbral para cada píxel según el método de Niblack.

Sintaxis: skimage.filters.threshold_niblack (imagen)

Parámetros:

• imagen : Una imagen – Formato monocromático
• window_size : Tamaño de ventana – entero impar
• k : Un parámetro positivo

Retorno: umbral: una máscara de umbral igual a la forma de la imagen

La función skimage.filters.threshold_sauvola() es una función de umbral local que devuelve un valor de umbral para cada píxel según el método de Sauvola.
 

Sintaxis: skimage.filters.threshold_sauvola(imagen)

Parámetros:

• imagen : Una imagen – Formato monocromático
• window_size : Tamaño de ventana – entero impar
• k : Un parámetro positivo
• r : Un parámetro positivo – rango dinámico de desviación estándar

Retorno: umbral: una máscara de umbral igual a la forma de la imagen

Código:

# Importing necessary libraries
from skimage import data
from skimage import filters
from skimage.color import rgb2gray
import matplotlib.pyplot as plt
 
# Setting plot size to 15, 15
plt.figure(figsize=(15, 15))
 
# Sample Image of scikit-image package
coffee = data.coffee()
gray_coffee = rgb2gray(coffee)
 
# Computing Otsu's thresholding value
threshold = filters.threshold_otsu(gray_coffee)
 
# Computing binarized values using the obtained
# threshold
binarized_coffee = (gray_coffee > threshold)*1
plt.subplot(2,2,1)
plt.title("Threshold: >"+str(threshold))
 
# Displaying the binarized image
plt.imshow(binarized_coffee, cmap = "gray")
 
# Computing Ni black's local pixel
# threshold values for every pixel
threshold = filters.threshold_niblack(gray_coffee)
 
# Computing binarized values using the obtained
# threshold
binarized_coffee = (gray_coffee > threshold)*1
plt.subplot(2,2,2)
plt.title("Niblack Thresholding")
 
# Displaying the binarized image
plt.imshow(binarized_coffee, cmap = "gray")
 
# Computing Sauvola's local pixel threshold
# values for every pixel - Not Binarized
threshold = filters.threshold_sauvola(gray_coffee)
plt.subplot(2,2,3)
plt.title("Sauvola Thresholding")
 
# Displaying the local threshold values
plt.imshow(threshold, cmap = "gray")
 
# Computing Sauvola's local pixel
# threshold values for every pixel - Binarized
binarized_coffee = (gray_coffee > threshold)*1
plt.subplot(2,2,4)
plt.title("Sauvola Thresholding - Converting to 0's and 1's")
 
# Displaying the binarized image
plt.imshow(binarized_coffee, cmap = "gray")

 Producción

Explicación: estas técnicas de establecimiento de umbrales locales utilizan la media y la desviación estándar como parámetros computacionales principales. Su valor de píxel local final también es felicitado por otros parámetros positivos. Esto se hace para asegurar la separación entre el objeto y el fondo. 
 

donde \bar x y \sigma representan la media y la desviación estándar de las intensidades de los píxeles, respectivamente.

Segmentación de contorno activa

El concepto de reducción funcional de energía sustenta el método de contorno activo. Un contorno activo es un enfoque de segmentación que utiliza fuerzas y restricciones de energía para separar los píxeles de interés del resto de la imagen para su posterior procesamiento y análisis. El término “contorno activo” se refiere a un modelo en el proceso de segmentación. 

La función skimage.segmentation.active_contour() activa los contornos ajustando serpientes a las características de la imagen

Sintaxis: skimage.segmentation.active_contour(imagen, serpiente)

Parámetros:

• imagen: una imagen
• serpiente : Coordenadas iniciales de la serpiente: para delimitar la función
• alfa: forma de longitud de serpiente
• beta : Forma de suavidad de serpiente
• w_line : Controla la atracción – Brillo
• w_edge : Controla la atracción – Bordes
• gamma : paso de tiempo explícito

Retorno: serpiente: serpiente optimizada con el tamaño del parámetro de entrada

Código:

# Importing necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from skimage.color import rgb2gray
from skimage import data
from skimage.filters import gaussian
from skimage.segmentation import active_contour
 
# Sample Image of scikit-image package
astronaut = data.astronaut()
gray_astronaut = rgb2gray(astronaut)
 
# Applying Gaussian Filter to remove noise
gray_astronaut_noiseless = gaussian(gray_astronaut, 1)
 
# Localising the circle's center at 220, 110
x1 = 220 + 100*np.cos(np.linspace(0, 2*np.pi, 500))
x2 = 100 + 100*np.sin(np.linspace(0, 2*np.pi, 500))
 
# Generating a circle based on x1, x2
snake = np.array([x1, x2]).T
 
# Computing the Active Contour for the given image
astronaut_snake = active_contour(gray_astronaut_noiseless,
                                 snake)
 
fig = plt.figure(figsize=(10, 10))
 
# Adding subplots to display the markers
ax = fig.add_subplot(111)
 
# Plotting sample image
ax.imshow(gray_astronaut_noiseless)
 
# Plotting the face boundary marker
ax.plot(astronaut_snake[:, 0],
        astronaut_snake[:, 1],
        '-b', lw=5)
 
# Plotting the circle around face
ax.plot(snake[:, 0], snake[:, 1], '--r', lw=5)

 Producción:

Explicación: el modelo de contorno activo se encuentra entre los enfoques dinámicos en la segmentación de imágenes que utiliza las restricciones y presiones de energía de la imagen para separar las regiones de interés. Para la segmentación, un contorno activo establece un borde o curvatura diferente para cada sección del objeto de destino. El modelo de contorno activo es una técnica para minimizar la función de energía resultante de fuerzas externas e internas. Una fuerza exterior se especifica como curvas o superficies, mientras que una fuerza interior se define como datos de imagen. La fuerza externa es una fuerza que permite que los contornos iniciales se transformen automáticamente en las formas de los objetos en las imágenes.

Segmentación Chan-Vese

El conocido método de segmentación iterativa de Chan-Vese divide una imagen en dos grupos con la varianza intraclase más baja. Este algoritmo utiliza conjuntos que evolucionan iterativamente para minimizar la energía, que se caracteriza por pesos correspondientes al total de variaciones en la intensidad del promedio general fuera de la región segmentada, la suma de las diferencias del promedio general dentro del vector de características y un término que es directamente proporcional a la longitud del borde de la región fragmentada.
 

La función skimage.segmentation.chan_vese() se usa para segmentar objetos usando el Algoritmo Chan-Vese cuyos límites no están claramente definidos.

Sintaxis: skimage.segmentation.chan_vese(imagen)

Parámetros:

• imagen: una imagen
• mu : Peso – Longitud del borde
• lambda1 : Peso – Diferencia del promedio
• tol : Tolerancia de variación del ajuste de nivel
• max_num_iter : Número máximo de iteraciones
• extended_output: se devuelve una tupla de 3 valores

Devolver :

• segmentación : Imagen segmentada
• phi: Conjunto de nivel final
• energías: Muestra la evolución de la energía

Código:

import matplotlib.pyplot as plt
from skimage.color import rgb2gray
from skimage import data, img_as_float
from skimage.segmentation import chan_vese
fig, axes = plt.subplots(1, 3, figsize=(10, 10))
 
# Sample Image of scikit-image package
astronaut = data.astronaut()
gray_astronaut = rgb2gray(astronaut)
 
# Computing the Chan VESE segmentation technique
chanvese_gray_astronaut = chan_vese(gray_astronaut,
                                    max_iter=100,
                                    extended_output=True)
 
ax = axes.flatten()
 
# Plotting the original image
ax[0].imshow(gray_astronaut, cmap="gray")
ax[0].set_title("Original Image")
 
# Plotting the segmented - 100 iterations image
ax[1].imshow(chanvese_gray_astronaut[0], cmap="gray")
title = "Chan-Vese segmentation - {} iterations".
format(len(chanvese_gray_astronaut[2]))
 
ax[1].set_title(title)
 
# Plotting the final level set
ax[2].imshow(chanvese_gray_astronaut[1], cmap="gray")
ax[2].set_title("Final Level Set")
plt.show()

Producción:

Explicación: el modelo de Chan-Vese para contornos activos es un enfoque sólido y versátil para segmentar una amplia gama de imágenes, incluidas algunas que serían difíciles de segmentar con métodos «tradicionales», como umbrales o métodos basados ​​en gradientes. Este modelo se usa comúnmente en imágenes médicas, particularmente para la segmentación del cerebro, el corazón y la tráquea. El modelo se basa en un problema de minimización de energía que puede reformularse en una formulación de conjunto de niveles para que el problema sea más fácil de resolver.
 

Segmentación no supervisada

Marcar límites 

Esta técnica produce una imagen con bordes resaltados entre áreas etiquetadas, donde las imágenes se segmentaron usando el método SLIC. 

La función skimage.segmentation.mark_boundaries() es devolver una imagen con límites entre las regiones etiquetadas.

Sintaxis: skimage.segmentation.mark_boundaries(imagen)

Parámetros:

• imagen: una imagen
• label_img: array de etiquetas con regiones marcadas
• color: color RGB de los límites
• outline_color: color RGB de los límites circundantes

Volver: marcado: una imagen con límites está marcada

Código:  

# Importing required boundaries
from skimage.segmentation import slic, mark_boundaries
from skimage.data import astronaut
 
# Setting the plot figure as 15, 15
plt.figure(figsize=(15, 15))
 
# Sample Image of scikit-image package
astronaut = astronaut()
 
# Applying SLIC segmentation
# for the edges to be drawn over
astronaut_segments = slic(astronaut,
                          n_segments=100,
                          compactness=1)
 
plt.subplot(1, 2, 1)
 
# Plotting the original image
plt.imshow(astronaut)
 
# Detecting boundaries for labels
plt.subplot(1, 2, 2)
 
# Plotting the ouput of marked_boundaries
# function i.e. the image with segmented boundaries
plt.imshow(mark_boundaries(astronaut, astronaut_segments))

Producción:

Explicación: Agrupamos la imagen en 100 segmentos con compacidad = 1 y esta imagen segmentada actuará como una array etiquetada para la función mark_boundaries(). Cada segmento de la imagen agrupada se diferencia por un valor entero y el resultado de mark_boundaries son los límites superpuestos entre las etiquetas.

Clustering iterativo lineal simple

Al combinar píxeles en el plano de la imagen según su similitud de color y proximidad, este método genera superpíxeles. El agrupamiento iterativo lineal simple es el enfoque más actualizado para segmentar superpíxeles y requiere muy poca potencia informática. En pocas palabras, la técnica agrupa píxeles en un espacio de plano de imagen y color de cinco dimensiones para crear superpíxeles pequeños y casi uniformes.

La función skimage.segmentation.slic() se usa para segmentar la imagen usando el agrupamiento k-means.

Sintaxis: skimage.segmentation.slic(imagen)

Parámetros:

• imagen: una imagen
• n_segments : Número de etiquetas
• Compacidad : Equilibra el color y la proximidad del espacio.
• max_num_iter : Número máximo de iteraciones

Devuelve: etiquetas: Máscara de enteros que indica las etiquetas de los segmentos.

Código:

# Importing required libraries
from skimage.segmentation import slic
from skimage.data import astronaut
from skimage.color import label2rgb
 
# Setting the plot size as 15, 15
plt.figure(figsize=(15,15))
 
# Sample Image of scikit-image package
astronaut = astronaut()
 
# Applying Simple Linear Iterative
# Clustering on the image
# - 50 segments & compactness = 10
astronaut_segments = slic(astronaut,
                          n_segments=50,
                          compactness=10)
plt.subplot(1,2,1)
 
# Plotting the original image
plt.imshow(astronaut)
plt.subplot(1,2,2)
 
# Converts a label image into
# an RGB color image for visualizing
# the labeled regions.
plt.imshow(label2rgb(astronaut_segments,
                     astronaut,
                     kind = 'avg'))

Producción:

Explicación: esta técnica crea superpíxeles al agrupar píxeles en el plano de la imagen en función de su similitud de color y cercanía. Esto se hace en un espacio 5-D, donde XY es la ubicación del píxel. Debido a que la mayor distancia posible entre dos colores en el espacio CIELAB está restringida, pero la distancia espacial en el plano XY depende del tamaño de la imagen, debemos normalizar las distancias espaciales para aplicar la distancia euclidiana en este espacio 5D. Como resultado, se creó una nueva medida de distancia que tiene en cuenta el tamaño de los superpíxeles para agrupar píxeles en este espacio 5D. 

Segmentación de Felzenszwalb 

Se calcula la eficiente segmentación de imágenes basada en gráficos de Felsenszwalb. Produce una sobresegmentación de una imagen RGB en la cuadrícula de la imagen utilizando un agrupamiento rápido basado en un árbol de expansión mínimo. Esto se puede usar para aislar características e identificar bordes. Este algoritmo utiliza la distancia euclidiana entre píxeles. La función skimage.segmentation.felzenszwalb() se utiliza para calcular la eficiente segmentación de imágenes basada en gráficos de Felsenszwalb.  

Sintaxis: skimage.segmentation.felzenszwalb(imagen)

Parámetros:

• imagen : una imagen de entrada
• escala : Valor más alto – clústeres más grandes
• sigma : Ancho del núcleo gaussiano
• min_size : Tamaño mínimo del componente

Devuelve: segment_mask: máscara de entero que indica las etiquetas de los segmentos. 

Código: 

# Importing the required libraries
from skimage.segmentation import felzenszwalb
from skimage.color import label2rgb
from skimage.data import astronaut
 
# Setting the figure size as 15, 15
plt.figure(figsize=(15,15))
 
# Sample Image of scikit-image package
astronaut = astronaut()
 
# computing the Felzenszwalb's
# Segmentation with sigma = 5 and minimum
# size = 100
astronaut_segments = felzenszwalb(astronaut,
                                  scale = 2,
                                  sigma=5,
                                  min_size=100)
 
# Plotting the original image
plt.subplot(1,2,1)
plt.imshow(astronaut)
 
# Marking the boundaries of
# Felzenszwalb's segmentations
plt.subplot(1,2,2)
plt.imshow(mark_boundaries(astronaut,
                           astronaut_segments))

Producción: 

Con la función mark_boundaries()

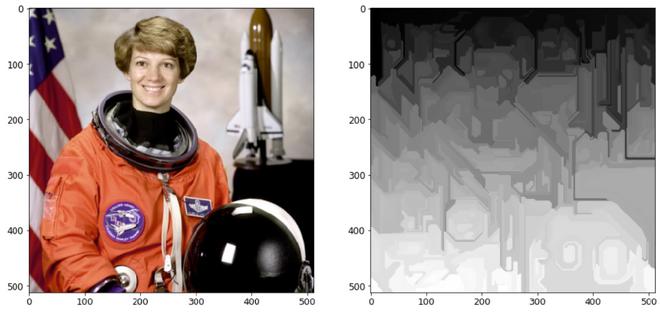
Sin función mark_boundaries()

Explicación: el uso de una agrupación en clústeres basada en una estructura de árbol mínima y rápida en la cuadrícula de imagen crea una segmentación excesiva de una imagen multicanal. La escala del parámetro determina el nivel de observación. Menos y más grandes partes están asociadas con una mayor escala. El diámetro de un núcleo gaussiano es sigma, que se utiliza para suavizar la imagen antes de la segmentación. La escala es la única forma de controlar la cantidad de segmentos generados, así como su tamaño. El tamaño de los segmentos individuales dentro de una imagen puede cambiar drásticamente según el contraste local.

Existen muchas otras técnicas de segmentación de imágenes supervisadas y no supervisadas. Esto puede ser útil para confinar características individuales, aislamiento de primer plano, reducción de ruido y puede ser útil para analizar una imagen de manera más intuitiva. Es una buena práctica segmentar las imágenes antes de construir un modelo de red neuronal para obtener resultados efectivos.