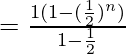Series geométricas

Un conjunto de cosas que están en orden se llama Secuencia y cuando las Secuencias comienzan a seguir un patrón determinado, se conocen como Progresiones . Las progresiones son de diferentes tipos, como progresiones aritméticas, progresiones geométricas, progresiones armónicas.

La suma de una Secuencia particular se llama Serie . Una Serie puede ser Infinita o Finita dependiendo de la Secuencia. Si una Secuencia es Infinita, dará una Serie Infinita mientras que, si una Secuencia es finita, dará una Serie Finita.

Tomemos una sucesión finita:

un _1, un _2, un _3, un _4, un _5,……….un _norte

La serie de esta secuencia se da como:

a ₁ + a ₂ + a ₃ + a ₄ + a ₅ +………….a _n

La serie también se denota como:

$\sum_{k=1}^{n}a_k$

La serie se representa usando la notación Sigma (∑) para indicar la suma.

En una serie geométrica, cada término siguiente es la multiplicación de su término anterior por una determinada constante y, según el valor de la constante, la serie puede ser creciente o decreciente.

La secuencia geométrica se da como:

a, ar, ar ² , ar ³ , ar ⁴ ,….. {Secuencia Infinita}

a, ar, ar ² , ar ³ , ar ⁴ , ……. ar ⁿ {Secuencia finita}

La serie geométrica para lo anterior se escribe como:

a + ar + ar ² + ar ³ + ar ⁴ +…. {Series infinitas}

a + ar + ar ² + ar ³ + ar ⁴ +….. ar ⁿ {Serie finita}

Dónde. a = Primer término

r = factor común

¿Pueden los valores de ‘a’ y ‘r’ ser 0?

Respuesta: No, el valor de a≠0, si el primer término se vuelve cero, la serie no continuará. Del mismo modo, r≠0.

Fórmula de serie geométrica

La fórmula de la serie geométrica para la serie finita se da como,

${S_n =\frac{a(1-r^n)}{1-r}}$

donde, S _{n =}^suma hasta el término n

a = Primer término

r = factor común

Derivación de la fórmula de la serie geométrica

Supongamos una Serie Geométrica para n términos:

S _norte = un + ar + ar ² + ar ³ + …. + ^n-1 ⇢ (1)

Multiplicando ambos lados por el factor común (r):

_r S norte = ar + ar ² + ar ³ + ar ⁴ + … + ar norte ^⇢ (2)

Restando la Ecuación (1) de la Ecuación (2):

(r S _n – S _n ) = (ar + ar ² + ar ³ + ar ⁴ + … ar ⁿ ) – (a + ar + ar ² + ar ³ +… + ar ^n-1 )

S norte ( _r -1) = ar ^norte – un

S norte (1 – _r ) = un (1-r ^norte )

${S_n =\frac{a(1-r^n)}{1-r}}$

Nota: Cuando el valor de k comienza desde ‘m’, la fórmula cambiará.

$\sum_{k=m}^{n}ar^k=\frac{a(r^m-r^{n+1}}{1-r}$ , cuando r≠0

Para series geométricas infinitas

n tenderá a Infinito, n⇢∞, Poniendo esto en la fórmula generalizada:

$S_\infty = \sum_{n=1}^{\infty}ar^{n-1} = \frac{a}{1-r}; -1<{r}<1$

N ^th término para el GP : a _n = ar ^n-1

Producto de la serie Geométrica

El Producto de todos los números presentes en la progresión geométrica nos da el producto total. Es muy útil al calcular la media geométrica de toda la serie.

Significado geometrico

Por definición, es la raíz ^enésima del Producto de n números donde ‘n’ denota el número de términos presentes en la serie. La Media Geométrica se diferencia de la Media Aritmética en que esta última se obtiene sumando todos los términos y dividiendo por ‘n’, mientras que la primera se obtiene haciendo el producto y luego sacando la media de todos los términos.

Importancia de la media geométrica

La media geométrica se calcula porque informa la composición que se produce de un período a otro. Indica el comportamiento central de la Progresión tomando la media de la Progresión geométrica. Por ejemplo, el crecimiento de bacterias se puede analizar fácilmente utilizando la media geométrica. En resumen, cuanto mayor sea el horizonte temporal o los valores de la serie difieren entre sí, la composición se vuelve más crítica y, por lo tanto, la media geométrica es más apropiada para usar.

Fórmula para la media geométrica

$\bar{X}_{geom}=\sqrt [n]{x_{1}.x_{2}.x_{3}...x_{n}}$

dónde,

$\bar{X}_{geom}=\text{symbol for Geometric mean}\\x_{1},x_{2},x_{3}...x_{n}=\text{terms present in the geometric series}\\n=\text{number of terms present in the series}$

Pregunta 1: ¿Cuál es la media geométrica 2, 4, 8?

Responder:

Según la fórmula,

$=\sqrt [3]{(2)(4)(8)}\\=4$

Pregunta 2: Encuentra el primer término y factor común en la siguiente Progresión Geométrica:

4, 8, 16, 32, 64,….

Responder:

Aquí, es claro que el primer término es 4, a=4

Obtenemos Razón común dividiendo el 1er término del 2do:

r = 8/4 = 2

Pregunta 3: Encuentra el término 8 y n ^{para el}^GP : 3, 9, 27, 81,….

Respuesta :

Ponga n=8 para el ^8vo término en la fórmula: ar ^n-1

Para el GP: 3, 9, 27, 81….

Primer término (a) = 3

Relación común (r) = 9/3 = 3

8 ^o término = 3(3) ^8-1 = 3(3) ⁷ = 6561

norte = 3(3) ^n-1⁼ 3(3) ⁿ (3) ^-1

= 3 ^norte

Pregunta 4: Para el médico de cabecera: 2, 8, 32,…. ¿Qué término dará el valor 131073?

Responder:

Suponga que el valor 131073 es el N ^-ésimo término,

a = 2, r = 8/2 = 4

N ^ésimo término (a _n ) = 2(4) ^n-1 = 131073

4 ^n-1 = 131073/2 = 65536

4 ^n-1 = 65536 = 4 ⁸

Igualando las potencias ya que la base es la misma:

n-1 = 8

norte = 9

^{Pregunta 5: Encuentra la suma} hasta el término 5 ^y N de la serie: $1, \frac{1}{2},\frac{1}{4},\frac{1}{8}...$

Responder:

a = 1, r = 1/2

Suma de N términos para el GP, ${S_n =\frac{a(1-r^n)}{1-r}}$

$= \frac{1(1-(\frac{1}{2})^n)}{1-\frac{1}{2}}$

$= 2 (1-(\frac{1}{2})^n)$

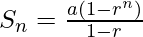
Suma de los primeros 5 términos ⇒ a ₅ = $2 ( 1-(\frac{1}{2})^5)$

= $2 ( 1-(\frac{1}{32}))$

= $(\frac{31}{16})$

Pregunta 6: Encuentra la Suma del Infinito GP: 0.5, 1, 2, 4, 8, …

Responder:

Fórmula para la Suma de Infinito GP: $\frac{a}{1-r}$ ; r≠0

a = 0,5, r = 2

S _∞ = (0,5)/(1-2) = 0,5/(-1)= -0,5

Pregunta 7: Encuentra la suma de la Serie: 5, 55, 555, 5555,… n términos

Respuesta :

La serie dada no está en GP, pero se puede convertir fácilmente en GP con algunas modificaciones simples.

Tomando 5 comunes de la serie: 5 (1, 11, 111, 1111,… n términos)

Dividir y multiplicar por 9: $\frac{5}{9}(9+ 99+ 999+...n terms)$

⇒ $\frac{5}{9}[((10+(10)^2+(10)^3+...n terms)-(1+1+1+...n terms)]$

⇒ $\frac{5}{9}[(\frac{10((10)^n-1)}{10-1})-(n)]$

⇒ $\frac{5}{9}[(\frac{10((10)^n-1)}{9})-(n)]$

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA