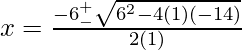Una identidad algebraica es una igualdad que se cumple para cualquier valor de sus variables. Generalmente se utilizan en la factorización de polinomios o la simplificación de cálculos algebraicos. Un polinomio es solo un conjunto de términos algebraicos que se suman, por ejemplo, p(x) = 4x + 1 es un polinomio de grado 1. Del mismo modo, los polinomios pueden ser de cualquier grado 1, 2, 3… y así sucesivamente. Los polinomios son básicamente aquellas expresiones matemáticas que facilitan los cálculos en la vida real. Hay diferentes tipos de polinomios dependiendo de la cantidad de términos presentes en ellos, por ejemplo, si hay 2 términos, se conoce como binomio.
ceros de polinomios
Supongamos que P(x) es un polinomio. Sea x = r, el valor de x donde nuestro polinomio P(x) se convierte en cero, es decir,
P(x) = 0 en x = r o P(r) = 0
El proceso de encontrar los ceros de P(x) es simplemente resolver la ecuación P(x) = 0. Ya sabemos cómo calcular ceros para polinomios de primer y segundo grado. Veamos algunos ejemplos de esto,
Pregunta 1: P(x) = x 2 + 2x – 15. Encuentra las raíces de este polinomio.
Solución:
Pongamos P(x) = 0,
x2 + 2x -15 = 0
⇒ x2 + 5x – 3x – 15 = 0
⇒ x(x+5) -3 (x+5) = 0
⇒ (x – 3) (x + 5) = 0
Entonces, esta expresión será cero para dos valores de x, es decir, x = 3 y -5.
El último ejemplo usó el método de factorización para encontrar las raíces del polinomio. También podemos usar otros métodos, como el factor cero de la fórmula cuadrática de Shree Dharacharya para encontrar las raíces o los ceros de un polinomio.
Si ax 2 + bx + c = 0, donde a≠0, entonces la fórmula para las raíces será,
Esta fórmula para encontrar las raíces de un polinomio se conoce como fórmula cuadrática de Shree Dharacharya.
Pregunta 2: Resuelve las raíces del polinomio, x 2 + 6x – 14 = 0
Solución:
Como está claro que la expresión anterior no se puede simplificar solo por intuición, por lo tanto, optaremos por la Fórmula Dharacharya.
Aquí, a=1, b=+6, c=-14
x=-3±√23
Significado geométrico de los ceros de un polinomio
Sabemos qué son los ceros, pero ¿por qué son importantes? Veamos la interpretación gráfica del significado detrás de los ceros. Veamos las gráficas de polinomios de primer y segundo grado.
Tomemos un polinomio y = 2x + 1, este también es una ecuación de una línea recta. La siguiente figura representa la gráfica de esta línea recta. Veremos las posiciones donde y se convierte en cero.

Este gráfico interseca el eje x en una posición, solo hay una raíz. Entonces, podemos concluir del gráfico que las raíces son la posición donde el gráfico del polinomio interseca al eje x.
Entonces, en general, para un polinomio y = ax + b, representa una línea recta con una raíz, que se encuentra en la posición donde el gráfico corta el eje x, es decir ( ![]() .
.
Ahora, veamos las gráficas de polinomios de segundo grado.
Sea p(x) = x 2 – 3x – 4, la siguiente figura representa su gráfica. Centrémonos en las raíces de este polinomio.

En este gráfico, podemos ver que corta el eje x en dos puntos. Entonces, estos dos puntos son los ceros de este polinomio. Pero, ¿será siempre así? Este gráfico puede estar orientado hacia arriba o hacia abajo según el coeficiente de x 2 .
En general, los ceros de un polinomio cuadrático ax 2 + bx + c, a ≠ 0, son precisamente las coordenadas x de los puntos donde la parábola que representa y = ax 2 + bx + c corta el eje x.
Tres posibles casos pueden ocurrir a la forma de la gráfica.
Caso (i): La gráfica corta el eje x en dos puntos distintos A y A′. Este es el caso que se ha mostrado arriba. Aquí el polinomio y = ax 2 + bx + c tiene dos raíces distintas.
Caso (ii): La gráfica corta el eje x exactamente en un punto, es decir, en dos puntos coincidentes. Dos mismas raíces. Aquí el polinomio y = ax 2 + bx + c tiene una sola raíz.

Caso (iii): El gráfico está completamente por encima del eje x o completamente por debajo del eje x. Aquí el polinomio y = ax 2 + bx + c no tiene raíces.

De manera similar, estudiemos esto para un polinomio cúbico .
Polinomio cúbico
Supongamos un polinomio, P(x) = x 3 – 4x.
P(x) = x( x2-4 )
= x(x-2)(x+2)
Entonces las raíces de este polinomio son x = 0, 2, -2.
Podemos verificar a partir del gráfico que estos deben ser los lugares donde la curva corta el eje x.

Pero como en el caso de los polinomios de segundo grado, puede haber más de una posibilidad.
Tomemos un ejemplo de polinomio cúbico P(x) = x 3

Este gráfico corta el eje x solo en un punto. Entonces, x = 0 es la única raíz del polinomio p(x) = x 3 .
Puede haber otro caso, por ejemplo, tomar P(x) = x 3 – x 2 .

Podemos ver que la gráfica de esta función corta el eje x solo en dos lugares. Del ejemplo anterior, podemos decir que este polinomio puede tener como máximo 3 ceros.
Nota: En general, un polinomio de grado “N” puede tener como máximo N ceros.
Pregunta 1: ¿Cuál de los siguientes gráficos representa un polinomio cúbico?

Responder:
(A) es la gráfica de un polinomio cúbico porque corta el eje x solo tres veces.
(B) no corta el eje x en absoluto y aumenta continuamente, por lo que no puede ser.
(C) Corta el eje x en más de 5 puntos. Entonces no puede ser un polinomio de tres grados.
(D) Es una gráfica de una parábola, que estudiamos antes. Entonces no es un polinomio cúbico.
Pregunta 2: Muestre los ceros de la ecuación cuadrática en el gráfico, x 2 – 3x – 4 = 0
Solución:
De la ecuación, podemos decir que hay 2 valores de x.
Factorizar la ecuación cuadrática para encontrar los valores de x,
x2-4x + x -4= 0
x(x-4) +1(x-4)= 0
X = (-1), X = 4
Por lo tanto, el gráfico será una parábola hacia arriba que se corta en (-1,0) y (4,0)
Pregunta 3: Encuentra el punto donde la gráfica interseca el eje x para la ecuación cuadrática, x 2 – 2x – 8 = 0
Solución:
Factorice la ecuación cuadrática para encontrar los puntos,
x2-4x + 2x -8 = 0
x(x-4) +2(x-4)= 0
(x-4)(x+2)= 0
x = 4, x = (-2)
Por lo tanto, la ecuación cortará la gráfica en el eje x en (4,0) y (-2,0)
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA