Simplifica {(2a + b)/(a – b)(a – 2 b)} – {(a + 4 b)/(a – b)(a – 3 b)} – {(a – 7 b)/ (a – 2 b)(a – 3 b)}

Anteriormente, allá por el siglo IX, las ecuaciones matemáticas que contenían cierta información solían escribirse en forma de lenguaje en lugar de forma matemática. Por ejemplo, 6 veces el número desconocido sumado a 9 da 39. Ahora bien, se puede ver claramente que escribir la ecuación en forma de lenguaje era muy largo ya veces demasiado complejo. Por lo tanto, con más y más teorías, desde el álgebra babilónica hasta las expresiones algebraicas modernas, las ecuaciones podrían escribirse matemáticamente en un formato más fácil y se denominan ecuaciones algebraicas.

Expresión algebraica

Una expresión algebraica es aquella que es una combinación de diferentes números sin especificarlos. En otras palabras, los números están siendo representados por diferentes variables unidas por algunos operadores matemáticos. Este tipo de expresiones se pueden resolver mediante varios métodos, como el método de acierto y prueba, el método directo, el método matricial, etc. Pero la forma más sencilla de resolverlas es mediante el método directo de resolución de expresiones algebraicas. Por ejemplo: una expresión algebraica simple se puede representar como: 

(a + b – c) / (10 × (a + b + c + 1)) = 0

Aquí, a, b y c son tres variables que representan tres números, y todas ellas están unidas por algún tipo de operador matemático. Entonces, esta es una expresión algebraica cuyas raíces/soluciones pueden o no existir. Ahora, consideremos el método directo para resolver una expresión algebraica resolviendo el siguiente problema: 

Simplifica:  .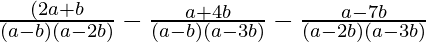

Solución:

Ahora, para simplificar la expresión algebraica dada. Esto se puede hacer fácilmente por el método directo. 

Paso 1: Tome MCM que es (a – b)(a – 2b)(a – 3b). Entonces la expresión dada se convierte en,

{(2a + b)(a – 3b)} – {(a + 4b)(a – 2b)} – {(a – 7b)(a – b)} / {(a – b)(a – 2b) (a-3b)}

Paso 2: resuelve la parte del numerador dejando la parte del denominador como está.

{(2a ² – 6ab + ab – 3b ² ) – (a ² – 2ab + 4ab – 8b ² ) – (a ² – ab – 7ab + 7b ² )} / {(a – b)(a – 2b)( a-3b)}

Paso 3: simplifica la parte del numerador nuevamente,

{(2a ² – 3b ² – 5ab – a ² + 8b ² – 2ab – a ² – 7b ² + 8ab)} / {(a – b)(a – 2b)(a – 3b)}

Paso 4: Al simplificar la parte del numerador,

(-2b ² + ab) / {(a – b)(a – 2b)(a – 3b)}

Paso 5: Ahora, tomando b como común del numerador, obtenemos la expresión como:

{b × (a – 2b)} / {(a – b)(a – 2b)(a – 3b)}

Paso 6: Como se puede ver claramente que (a – 2b) está presente tanto en el numerador como en el denominador. Entonces, ambos se cancelan entre sí y, por lo tanto, este término se puede eliminar tanto del numerador como del denominador. Entonces, después de eliminar el término (a – 2b) tanto del numerador como del denominador, la expresión es:

b / {(a-b)(a-3b)}

Entonces, esta es la forma más simple de la expresión dada que se obtiene por el método directo. Ahora, esta expresión se puede usar donde sea necesario y, por lo tanto, será más fácil resolver otras expresiones, incluida esta.

Problemas similares

Pregunta 1: simplifica la expresión algebraica: {c(a – b) / (a ^​​2 – b ² )} + c / (a ​​+ b)

Solución: 

Paso 1: La identidad (a ² – b ² ) = (a + b)(a – b) ya se conoce. Así que poniendo esta identidad en la expresión dada,

{c(a – b) / {(a – b)(a + b)}} + c / (a ​​+ b)

Paso 2: sacando el valor común (a – b) tanto del numerador como del denominador del primer término, 

c/(a + b) + c/(a + b)

Paso 3: dado que ambos términos son iguales, súmalos directamente y, por lo tanto, la expresión final se convierte en:

2 × c / (a ​​+ b)

Pregunta 2: simplifica la expresión algebraica: {(a ² + 2ab + b ² ) / (a ​​+ b)} – b + {a ² / (a ​​+ b)}

Solución: 

Paso 1: La identidad (a + b) ² = a ² + 2ab + b ² ya se conoce. Entonces, poniendo esta identidad en la parte del numerador del primer término de la expresión dada, 

{(a + b) ² / (a ​​+ b)} – b + {a ² / (a ​​+ b)}

Paso 2: En el primer término de la expresión, toma (a + b) como común y así se puede quitar tanto del numerador como del denominador. Así que la expresión ahora se convierte en,

9(a + b) – b + {a ² / (a ​​+ b)}

Paso 3: Dado que + b – b se convierte en 0, entonces:

a + {a ² / (a ​​+ b)}

Paso 4: Deje la expresión aquí o haga un paso más tomando el MCM y resolviendo más. Entonces, si el MCM se lleva más allá de esta expresión: 

(2a ² + ab) / (a ​​+ b)

Paso 5: Tomando a como común de la parte del numerador de la expresión, la expresión algebraica simplificada final es: 

a × (2a + b) / (a ​​+ b)