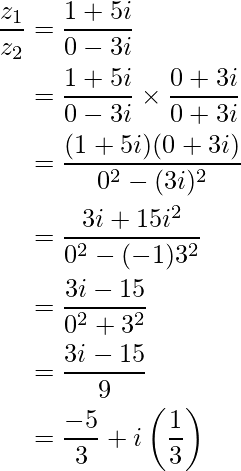Simplifica y escribe en forma estándar (1 + 5i)/-3i

Los números complejos son aquellos con la fórmula a + ib, donde a y b son números reales y I (iota) es el componente imaginario y representa (-1), y a menudo se representan en forma de rectángulo o estándar. 10 + 5i, por ejemplo, es un número complejo en el que 10 representa la componente real y 5i representa la parte imaginaria. Dependiendo de los valores de a y b, pueden ser completamente reales o puramente ficticios. Cuando a = 0 en a + ib, ib es un número totalmente imaginario, y cuando b = 0, obtenemos a, que es un número estrictamente real.

Dividir dos números complejos

El proceso de división de dos números complejos es ligeramente diferente al proceso de división de dos números reales. Dividir números complejos es más como el concepto de racionalizar el denominador en el caso de fracciones que involucran números irracionales como sus denominadores.

Los siguientes pasos están involucrados:

Asegúrese de que tanto el numerador como el numerador estén en la forma estándar de números complejos, es decir, z = a + ib.
Calcula el complejo conjugado del denominador. Digamos, si el denominador es c + id, entonces su conjugado es c − id.
Multiplica el conjugado con ambos términos de la fracción.
Usa la fórmula de la diferencia de cuadrados para resolver el denominador.
Divide el número complejo obtenido en sus partes real e imaginaria.

El proceso de división de dos números complejos z ₁ = x + iy y z ₂ = a + ib se muestra a continuación:

$\begin{aligned}\dfrac{z_1}{z_2}&=\dfrac{x+iy}{a+ib}\\&=\dfrac{x+iy}{a+ib}\times\dfrac{a-ib}{a-ib}\\&=\dfrac{(x+iy)(a-ib)}{a^2-(ib)^2}\\&=\dfrac{ax-ibx+iay-i^2by}{a^2-(-1)b^2}\\&=\dfrac{ac-ibx+iay+by}{a^2+b^2}\\&=\dfrac{(ax+by)+i(ay-bx)}{a^2+b^2}\\&=\dfrac{ax+by}{a^2+b^2}+i\left(\dfrac{ay-bx}{a^2+b^2}\right)\end{aligned}$

Simplifica y escribe la respuesta en forma estándar (1 + 5i)/-3i.

Solución:

Forma estándar del denominador −3i = 0 − 3i

Conjugado del denominador = 0 + 3i

Multiplica tanto el numerador como el denominador por 0 + 3i.

$\begin{aligned}\dfrac{z_1}{z_2}&=\dfrac{1+5i}{0-3i}\\&=\dfrac{1+5i}{0-3i}\times\dfrac{0+3i}{0+3i}\\&=\dfrac{(1+5i)(0+3i)}{0^2-(3i)^2}\\&=\dfrac{3i+15i^2}{0^2-(-1)3^2}\\&=\dfrac{3i-15}{0^2+3^2}\\&=\dfrac{3i-15}{9}\\&=\dfrac{-5}{3}+i\left(\dfrac{1}{3}\right)\end{aligned}$

Problemas similares

Problema 1. Resuelve: $\frac{-3-5i}{2i}$ .

Solución:

Forma estándar del denominador 2i = 0 + 2i

Conjugado del denominador = 0 − 2i

Multiplica tanto el numerador como el denominador por 0 + 2i.

$\begin{aligned}\dfrac{z_1}{z_2}&=\dfrac{-3-5i}{0+2i}\\&=\dfrac{-3-5i}{0+2i}\times\dfrac{0-2i}{0-2i}\\&=\dfrac{(-3-5i)(0-2i)}{0^2-(2i)^2}\\&=\dfrac{-5}{2}+i\left(\dfrac{3}{2}\right)\end{aligned}$

Problema 2. Resuelve: $\frac{-1}{3+2i}$ .

Solución:

Conjugado del denominador = 3 + 2i

Multiplica tanto el numerador como el denominador por 3 – 2i.

$\begin{aligned}\dfrac{z_1}{z_2}&=\dfrac{-1}{3+2i}\\&=\dfrac{-1}{3-2i}\times\dfrac{3+2i}{3+2i}\\&=\dfrac{(-3+2i)}{3^2-(2i)^2}\\&=\dfrac{-3}{13}+i\left(\dfrac{2}{13}\right)\end{aligned}$

Problema 3. Resuelve: $\frac{1}{3+2i}$ .

Solución:

Conjugado del denominador = 3 + 2i

Multiplica tanto el numerador como el denominador por 3 – 2i.

$\begin{aligned}\dfrac{z_1}{z_2}&=\dfrac{1}{3+2i}\\&=\dfrac{1}{3-2i}\times\dfrac{3+2i}{3+2i}\\&=\dfrac{(3+2i)}{3^2-(2i)^2}\\&=\dfrac{3}{13}+i\left(\dfrac{2}{13}\right)\end{aligned}$

Problema 4. Resuelve (5+√2i)/(1−√2i).

Solución:

Conjugado de denominador = 1 + √2i

Multiplica tanto el numerador como el denominador por 1 + √2i.

$\begin{aligned}\dfrac{5+\sqrt{2}i}{1-\sqrt{2}i}=\dfrac{a+ib}{c+id}&=\dfrac{ac+bd}{c^2+d^2}+i\left(\dfrac{bc-ad}{c^2+d^2}\right)\\&=\dfrac{(5\times 1)+(\sqrt{2}\times(-\sqrt{2}))}{1^2+(-\sqrt{2})^2}+\\&i\left(\dfrac{(\sqrt{2} \times 1)-(5\times(-\sqrt{2}))}{1^2+(-\sqrt{2})^2}\right)\\&=\dfrac{5-2}{1+2}+i\left(\dfrac{\sqrt{2}+5\sqrt{2}}{1+2}\right)\\&=\dfrac{3+6\sqrt{2}i}{1+2}\\&=1+2\sqrt{2}i\end{aligned}$

Problema 5. Resuelve: $\frac{1-5i}{-3i}$ .

Solución:

Forma estándar del denominador −3i = 0 − 3i

Conjugado del denominador = 0 + 3i

Multiplica tanto el numerador como el denominador por 0 + 3i.

$\begin{aligned}\dfrac{z_1}{z_2}&=\dfrac{1-5i}{0-3i}\\&=\dfrac{1-5i}{0-3i}\times\dfrac{0+3i}{0+3i}\\&=\dfrac{(1-5i)(0+3i)}{0^2-(3i)^2}\\&=\dfrac{3i-15i^2}{0^2-(-1)3^2}\\&=\dfrac{3i+15}{0^2+3^2}\\&=\dfrac{3i+15}{9}\\&=\dfrac{5}{3}+i\left(\dfrac{1}{3}\right)\end{aligned}$

Publicación traducida automáticamente

Artículo escrito por parmaramolaksingh1955 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Dividir dos números complejos

Simplifica y escribe la respuesta en forma estándar (1 + 5i)/-3i.

Problemas similares

Deja una respuesta Cancelar la respuesta