Simplificar 4ab2(-5ab3)/10a2b2

El sistema numérico es una idea matemática con la que todos estamos familiarizados. En la recta numérica, hay números ilimitados. En matemáticas, existen números/cantidades grandes y pequeñas que no pueden representarse explícitamente como tales. La idea de exponentes y potencias entra en escena en este punto.

Exponentes y Potencias

El número de veces que un número ha sido multiplicado por sí mismo se representa por su exponente. Por ejemplo, si 4 se multiplica por sí mismo n veces, el resultado es:

4 × 4 × 4 × 4 × 4 × 4 × …….. × norte = 4 ^norte

El exponente de 2 es n, y la fórmula 2n se escribe como 2 elevado a la potencia n. Como resultado, hay poca diferencia entre los exponentes y las potencias de las palabras, porque ambos expresan el mismo concepto.

leyes exponenciales

Ley de la Multiplicación: El producto de dos exponentes con la misma base pero potencias diferentes es igual a la base elevada al total de las dos potencias o números enteros, según la ley de la multiplicación de exponentes.

pags ^metro × pags norte = pags ^metro+ⁿ

Ley de división: La base se eleva a la diferencia entre las dos potencias cuando se dividen dos exponentes con las mismas bases pero potencias diferentes.

pag ^metro ÷ pag norte = pag ^metro-ⁿ

Ley de la Potencia Negativa: La Ley de la Potencia Negativa establece que si una base tiene una potencia negativa, producirá un recíproco con una potencia positiva o un número entero a la base.

p – ^m = 1/p ^m

Reglas exponenciales

Según esta regla, si la potencia de cualquier número es cero, el resultado será la unidad o uno.

pag ⁰ = 1

Diferentes bases con igual potencia en la multiplicación se multiplican junto con el exponente puesto en el producto.

pags ^metro × q ^metro = (pags × q) ^metro

El poder del poder se multiplica por el primero.

(p ^m ) ⁿ = p ^min

Simplificar 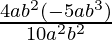$\frac{4ab^2(-5ab^3)}{10a^2b^2}$

Solución:

Multiplica los términos en el numerador, usando la ley de multiplicación de exponentes.

$\frac{4ab^2(-5ab^3)}{10a^2b^2}$ = $\frac{-20(a)^{1+1}(b)^{2+3}}{10a^2b^2}$

= $\frac{-2a^2b^5}{a^2b^2}$

Ahora aplica la ley de división de exponentes para evaluar.

= -2a ^2-2 b ^5-2

= -2a ⁰ b ³

= -2b ³

Problemas similares

Problema 1: Simplifica: 1/2x ^-99 .

Solución:

Usando la propiedad a ^-m = 1/a ^m , que se conoce como la ley del exponente negativo,

1/ 2x ^-99 = $\frac{1}{2}x^{99}$

= x ⁹⁹ /2.

Problema 2: Simplifica: 4/3x ^-9 .

Solución:

Usando la propiedad a ^-m = 1/ a ^m , que se conoce como la ley del exponente negativo,

4/3x ^-9 = $\frac{4}{3}x^9$

Problema 3: Simplifica: 12x ⁹ /51x ⁶⁰ .

Solución:

Usando la propiedad a ^m /a ⁿ = a ^{m – n} , que se conoce como la ley del cociente,

12×9 / ^5×60 = ^_ $\frac{12x^{9-60}}{5^1}$

= $12x^{-51}/5^1$

Usando la propiedad a ^-m = 1/ a ^m , que se conoce como la ley del exponente negativo,

$12x^{-51}/51 = \frac{12}{51x^{51}}$ .

Problema 4: Simplifica: 3x ² /10x ⁵ .

Solución:

Usando la propiedad a ^m / a ⁿ = a ^m-n , que se conoce como la ley del cociente,

3×2 / ¹⁰ ×5 = $\frac{3x^{2-5}}{10}$

= 3x ^-3 / 5

Usando la propiedad a ^-m = 1/ a ^m , que se conoce como la ley del exponente negativo,

3x ^-3 / 5 = $\frac{3}{10x^{3}}$

Problema 5: Simplifica: 2x ⁴ /5y ^-10 .

Solución:

Usando la propiedad a ^-m = 1/ a ^m , que se conoce como la ley del exponente negativo,

2x ⁴ / 5y ^-10 = $\frac{2x^4y^{10}}{5}$

Publicación traducida automáticamente

Artículo escrito por parmarraman44 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Exponentes y Potencias

leyes exponenciales

Reglas exponenciales

Simplificar

Problemas similares

Deja una respuesta Cancelar la respuesta

Simplificar $\frac{4ab^2(-5ab^3)}{10a^2b^2}$