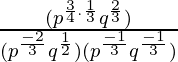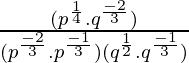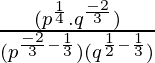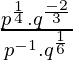Simplificar [(p3/4q-2)1/3]/[(p-2/3q1/2)(pq)-1/3]

El álgebra es una disciplina de las matemáticas que se ocupa del estudio de varios símbolos que representan cantidades que no tienen un valor fijo o una cantidad asociada con ellas, sino que varían o cambian con el tiempo en relación con algún otro factor. En el estudio del álgebra, estos símbolos se conocen como variables y los números asociados con ellos se denominan coeficientes. Se pueden representar en una variedad de formas, incluidas formas e incluso alfabetos en inglés. En otras palabras, el álgebra estudia la representación de números usando letras o símbolos en lugar de la representación de sus valores reales.

expresiones en algebra

En matemáticas, una expresión algebraica es una declaración que se construye utilizando variables y constantes, así como numerosas operaciones aritméticas como suma, resta, multiplicación, división, operaciones exponenciales, extracción de raíz como raíz cuadrada, raíz cúbica, raíz cuarta y pronto.

Ejemplos:

x + 22 es una expresión algebraica en la que x es la variable.

x − y + 69 es una expresión algebraica que involucra las variables x e y y la operación suma.

7x ² + 5xy + 44 es una expresión algebraica que involucra las variables x e y y las operaciones de suma, exponente, resta y multiplicación.

Términos básicos

Variable: En una expresión algebraica, una variable es una frase que puede tomar cualquier valor; su verdadero valor no existe.
Coeficiente: Es una constante bien definida que siempre se usa con una variable.
Operador: cualquier operación matemática, como suma, resta, multiplicación, división, operaciones exponenciales, extracción de raíz, como raíz cuadrada, raíz cúbica, raíz cuarta, etc., se denomina operador.
Constante: La constante es una palabra que es independiente tanto del coeficiente como de la variable y está bien definida en sí misma.

Reglas exponenciales

Regla 1: En la multiplicación, si dos o más bases tienen las mismas potencias, sus potencias se suman manteniendo la base intacta, es decir,

un ^metro × un norte = un ^metro+ⁿ

Regla 2: Si dos o más bases en la división tienen las mismas potencias, sus potencias se suman para mantener la base intacta. Cabe señalar que la potencia del denominador se resta de la potencia del numerador, es decir,

am ÷ an = a ^m-n

Regla 3: Cualquier cosa multiplicada por una potencia de cero es igual a uno.

un ⁰ = 1

Regla 4: La potencia de una potencia se multiplica por la original manteniendo intacta la base.

(un ^m ) ⁿ = un ^mn

Regla 5: Si dos bases separadas tienen la misma potencia, multiplíquelas y eleve el producto a la potencia que tenían ambas bases antes de la multiplicación, es decir

un ^metro × segundo ^metro = (ab) ^metro

Regla 6: Si se especifica un exponente fraccionario, el numerador se convierte en la potencia de la base y el denominador se convierte en la raíz de la expresión completa, es decir

un ^m/n = $\sqrt[n]{a^m}$

Regla 7: Intercambia la base para hacer que la potencia sea positiva, es decir

a ^-m = $\frac{1}{a^m}$

Simplificar 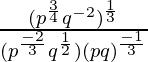$\frac{(p^\frac{3}{4}q^{-2})^\frac{1}{3}}{(p^\frac{-2}{3}q^\frac{1}{2})(pq)^\frac{-1}{3}}$

Solución:

Aplicar la regla: (a ^m .b ^m ) ⁿ = a ^mn b ^mn

= $\frac{(p^{\frac{3}{4}.\frac{1}{3}}q^\frac{2}{3})}{(p^\frac{-2}{3}q^\frac{1}{2})(p^\frac{-1}{3}q^\frac{-1}{3})}$

= $\frac{(p^{\frac{1}{4}}.q^\frac{-2}{3})}{(p^\frac{-2}{3}.p^\frac{-1}{3})(q^\frac{1}{2}.q^\frac{-1}{3})}$

Aplica la regla: a ^m × a ⁿ = a ^m+n en el denominador.

= $\frac{(p^{\frac{1}{4}}.q^\frac{-2}{3})}{(p^{\frac{-2}{3}-\frac{1}{3}})(q^{\frac{1}{2}-\frac{1}{3}})}$

= $\frac{(p^{\frac{1}{4}}.q^\frac{-2}{3})}{(p^{\frac{-3}{3}})(q^{\frac{1}{6}})}$

= $\frac{p^{\frac{1}{4}}.q^\frac{-2}{3}}{p^{-1}.q^{\frac{1}{6}}}$

Aplicar la regla a ^m ÷ a ⁿ = a ^m-n

= ${p^{\frac{1}{4}+1}.q^{\frac{-2}{3}-\frac{1}{6}}}$

= ${p^{\frac{5}{4}}.q^{\frac{-5}{6}}}$

Aplica la regla: a ^-m = $\frac{1}{a^m}$

= $\frac{{p^{\frac{5}{4}}}}{q^{\frac{5}{6}}}$

Por lo tanto, [(p ^3/4 q ^-2 ) ^1/3 ]/[(p ^-2/3 q ^1/2 )(pq) ^-1/3 ] = p ^5/4 /q ^5/6

Problemas similares

Pregunta 1. Simplifica: (x ^-7 y ¹⁰ ) (x ^-8 y ³ )

Solución:

= (x ^-7 x ^-8 ) (y ¹⁰ y ³ )

Aplicar una ^m . un norte = un ^m+ⁿ

= x ^-7-8 y ¹⁰⁺³

= x ^-15 y ¹³

Aplicar a ^-m = 1/ a ^m

= y ¹³ / x ¹⁵

Pregunta 2. Simplifica: $\frac{3x^2y^3}{5x^3y^2}$

Solución:

= 3/5 (x2 / ^x3 ) ( ^y3 / ^y2⁾

= 3/5 ( ^x2-3 ) ( ^y3-2 )

= 3/5 (x- ¹ ) ( ^y1 )

Aplicar a ^-m = 1/ a ^m

= 3y/5x

Pregunta 3. Simplifica y escribe como exponentes positivos: (64x ^-6 y ⁶ ) ^5/6 .

Solución:

Aplicar (abc) ^m = a ^m b ^m c ^m

(64x ^-6 y ⁶ ) ^5/6 = 64 ^5/6 x ^-30/6 y ^30/6

= 2 ⁵ x ^-6 y ⁵

Aplicar a ^-m = 1/a ^m

Por tanto, (64x ^-6 y ⁶ ) ^5/6 = 32y ⁵ / x ⁶

Pregunta 4. Simplifica y escribe como exponentes positivos: $\frac{2x^{-10}}{4y^0}$ .

Solución:

Como un ⁰ = 1.

Por lo tanto, 4y ⁰ = 1

Tenemos: 2x ^-10 / 1 = 2x ^-10

Aplicar a ^-m = 1/a ^m

Por lo tanto, $\frac{2x^{-10}}{4y^0}$ = 2/x ¹⁰ .

Pregunta 5. Simplifica: $[\frac{(2a^3)}{(3a^5)^3}]^3$ .

Solución:

Aplicando (a ^m ) ⁿ = a ^mn , tenemos:

[(2a ³ )/ (3a ^{5 × 3} ] ³ = [(2a ³ )/ (3a ¹⁵ ] ³

Usando la propiedad a ^m /a ⁿ = a ^m-n , tenemos:

= 2/3[un ^3-15 ] ³

= [2[a ^-12 ] ³ ]/3

= 2a ^-36 /3

Por lo tanto, [(2a ³ )/ (3a ⁵ ) ³ ] ³ = $\frac{2}{3a^{36}}.$

Publicación traducida automáticamente

Artículo escrito por parmaramolaksingh1955 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

expresiones en algebra

Reglas exponenciales

Simplificar

Problemas similares

Deja una respuesta Cancelar la respuesta

Simplificar $\frac{(p^\frac{3}{4}q^{-2})^\frac{1}{3}}{(p^\frac{-2}{3}q^\frac{1}{2})(pq)^\frac{-1}{3}}$