Sistema Numérico en Matemáticas

El sistema numérico es un método para representar números en la recta numérica con la ayuda de un conjunto de símbolos y reglas. Estos símbolos van del 0 al 9 y se denominan dígitos. Number System se utiliza para realizar cálculos matemáticos que van desde grandes cálculos científicos hasta cálculos como contar la cantidad de juguetes para niños o chocolates numéricos que quedan en la caja. Los sistemas numéricos comprenden múltiples tipos basados ​​en el valor base de sus dígitos. 

¿Qué es la recta numérica?

Una recta numérica es una representación de números con un intervalo fijo entre ellos en una línea recta. Una recta numérica contiene todos los tipos de números, como números naturales, racionales, enteros, etc. Los números en la recta numérica aumentan al moverse de izquierda a derecha y disminuyen al moverse de derecha a izquierda. Los extremos de una recta numérica no están definidos, es decir, los números en una recta numérica van desde infinito en el lado izquierdo del cero hasta infinito en el lado derecho del cero. 

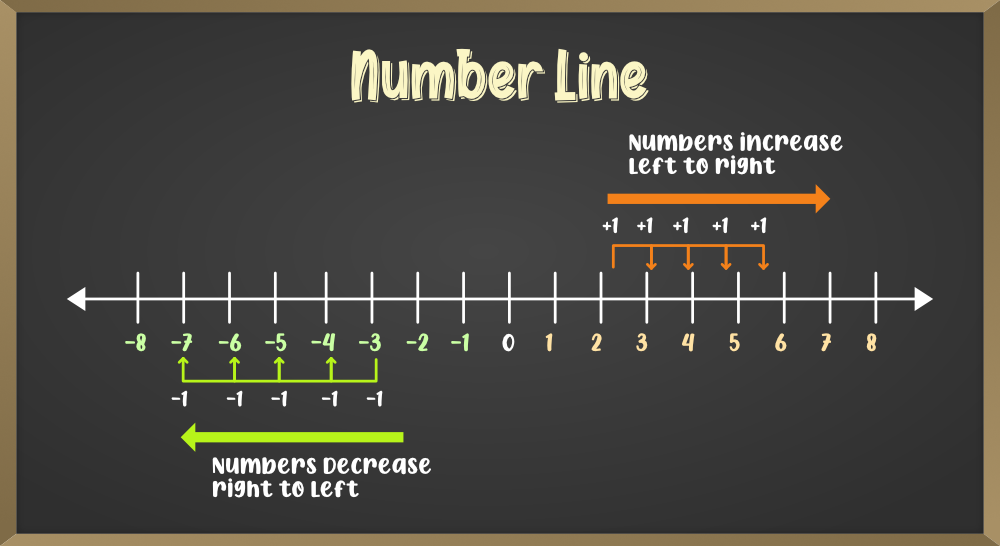
Números positivos: los números que se representan en el lado derecho del cero se denominan números positivos. El valor de estos números aumenta al moverse hacia la derecha. Los números positivos se utilizan para la Suma entre números. Ejemplo: 1, 2, 3, 4, …

Números negativos: los números que se representan en el lado izquierdo del cero se denominan números negativos. El valor de estos números disminuye al moverse hacia la izquierda. Los números negativos se utilizan para restar entre números. Ejemplo: -1, -2, -3, -4, …

Número y sus tipos

Un número es un valor creado por la combinación de dígitos con la ayuda de ciertas reglas. Estos números se utilizan para representar cantidades aritméticas. Un dígito es un símbolo de un conjunto de 10 símbolos que van desde 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9. Cualquier combinación de dígitos representa un número. El tamaño de un Número depende de la cantidad de dígitos que se utilizan para su creación.

Por ejemplo: 123, 124, 0,345, -16, 73, 9, etc. 

Tipos de números

Los números son de varios tipos según los patrones de dígitos que se utilizan para su creación. También se aplican varios símbolos y reglas a los Números que los clasifican en una variedad de tipos diferentes:

 

1. Números naturales: los números naturales son el tipo más básico de números que van del 1 al infinito. Estos números también se llaman números positivos o números de conteo. Los números naturales se representan con el símbolo  N.

Example:1, 2, 3, 4, 5, 6, 7, and so on.

2. Números Enteros: Los Números Enteros son básicamente los Números Naturales, pero también incluyen el ‘cero’. Los números enteros se representan con el símbolo  W.

Example:0, 1, 2, 3, 4, and so on.

3. Números enteros: los números enteros son la colección de números enteros más los valores negativos de los números naturales. Los números enteros no incluyen números fraccionarios, es decir, no se pueden escribir en forma a/b. El rango de números enteros es desde el infinito en el extremo negativo hasta el infinito en el extremo positivo, incluido el cero. Los números enteros se representan con el símbolo Z.

Example: ...,-4, -3, -2, -1, 0, 1, 2, 3, 4,...

4. Fracciones: Las fracciones son los números que se escriben en forma de a/b, donde a pertenece a los números enteros y b pertenece a los números naturales, es decir, b nunca puede ser 0. La parte superior de la fracción, es decir, a es denominado numerador, mientras que la parte inferior, es decir, b, se denomina denominador. 

Example:1/2, 3/7, 8/3, etc.

5. Números racionales: Los números racionales son los números que se pueden representar en forma de fracción, es decir, a/b. Aquí, a y b son enteros y b

6. Números irracionales: Los números irracionales son los números que no se pueden representar en forma de fracciones, es decir, no se pueden escribir como a/b. 

Example:π... 

7. Números reales e imaginarios: Los números reales son los números que se pueden representar en forma decimal. Estos números incluyen números enteros, enteros, fracciones, etc. Todos los números enteros pertenecen a los números reales, pero no todos los números reales pertenecen a los números enteros. 

Los números imaginarios son todos aquellos números que no son números reales. Estos números cuando se elevan al cuadrado darán como resultado un número negativo. los

Example:

Los números que no tienen más factores que 1 y el número en sí se denominan números primos. Todos los números que no sean números primos se denominan números compuestos, excepto el 0. El cero no es ni primo ni compuesto. 

Example: 2, 3, 5, 7,... are prime numbers and 4, 6, 8, 9, 12,... are composite numbers

Tipos de sistemas numéricos

Según el valor base y la cantidad de dígitos permitidos, los sistemas numéricos son de muchos tipos. Los cuatro tipos comunes de sistemas numéricos son: 

1. Sistema de números decimales
2. Sistema de números binarios
3. Sistema de numeración octal
4. Sistema numérico hexadecimal

1. Sistema de números decimales

El sistema numérico con valor base 10 se denomina sistema numérico decimal. Utiliza 10 dígitos, es decir, 0-9 para la creación de números. Aquí, cada dígito en el número está en un lugar específico con valor posicional producto de diferentes potencias de 10. Aquí, el valor posicional se denomina de derecha a izquierda como el primer valor posicional llamado unidades, el segundo a la izquierda como decenas, y así sucesivamente. Centenas, Millares, etc. Aquí, las unidades tienen el valor posicional de 10 ⁰ , las decenas tienen el valor posicional de 10 ¹ , las centenas son 10 ² , las miles son 10 ³ , y así sucesivamente. 

Por ejemplo: 10285 tiene valores posicionales como

(1 × 10 ⁴ )+ (0 × 10 ³ ) + (2 × 10 ² ) + (8 × 10 ¹ ) + (5 × 10 ⁰ )

1 × 10000 + 0 × 1000 + 2 × 100 + 8 × 10 + 5 × 1

10000 + 0 + 200 + 80 + 5

10285

2. Sistema numérico binario

El sistema numérico con valor base 2 se denomina sistema numérico binario. Utiliza 2 dígitos, es decir, 0 y 1 para la creación de números. Los números formados con estos dos dígitos se denominan números binarios. El sistema de números binarios es muy útil en dispositivos electrónicos y sistemas informáticos porque se puede realizar fácilmente usando solo dos estados ON y OFF, es decir, 0 y 1. 

Los números decimales del 0 al 9 se representan en binario como: 0, 1, 10, 11, 100, 101, 110, 111, 1000 y 1001

Ejemplos:

14 se puede escribir como 1110

19 se puede escribir como 10011

50 se puede escribir como

la

representado como AF, es decir, 10 se representa como A, 11 como B, 12 como C, 13 como D, 14 como E y 15 como F. ​​Los números hexadecimales son útiles para manejar ubicaciones de direcciones de memoria. 

Ejemplos: 

(255) ₁₀ se puede escribir como (FF) ₁₆

(1096) ₁₀ se puede escribir como (448) ₁₆

(4090) ₁₀ se puede escribir como (FFA) ₁₆

Conversión de sistemas numéricos

La conversión entre sistemas de números es una tarea bastante fácil. Cualquier número de cualquier sistema numérico se puede convertir a otros sistemas numéricos con la ayuda de ciertos métodos que se discutirán a continuación:

1. Conversión del sistema numérico decimal a otros sistemas numéricos

Los números decimales se representan con dígitos del 0 al 9 y con base 10. La conversión de un sistema numérico significa la conversión de una base a otra. A continuación se muestra la conversión del sistema numérico decimal a otros sistemas numéricos:

A. Conversión de decimal a binario: 

Los números decimales se representan en base 10, pero los números binarios son de base 2. Por lo tanto, para convertir un número decimal a número binario, se debe cambiar la base de ese número. Siga los pasos que se indican a continuación:

• Paso 1: divide el número decimal con la base del sistema numérico al que se convertirá. Aquí la conversión es a binario, por lo que el divisor será 2. 
• Paso 2: El resto obtenido de la división se convertirá en el dígito menos significativo del nuevo número.
• Paso 3: El cociente obtenido de la división se convertirá en el siguiente dividendo y se dividirá por la base, es decir, 2.
• Paso 4: El resto obtenido pasará a ser el segundo dígito menos significativo, es decir, se sumará a la izquierda del dígito obtenido anteriormente.

Ahora, se repiten los pasos 3 y 4 hasta que el cociente obtenido sea 0, y se suman a la izquierda de los dígitos existentes los residuos obtenidos tras cada iteración. 

Una vez finalizadas todas las iteraciones, el último resto obtenido se denominará dígito más significativo.

B. Conversión de decimal a octal:

Los números octales se representan en base 8. Por lo tanto, para convertir un número decimal en un número octal, se debe cambiar la base de ese número. Siga los pasos que se indican a continuación:

• Paso 1: divide el número decimal con la base del sistema numérico al que se convertirá. Aquí la conversión es a octal, por lo que el divisor será 8. 
• Paso 2: El resto obtenido de la división se convertirá en el dígito menos significativo del nuevo número.
• Paso 3: El cociente obtenido de la división se convertirá en el siguiente dividendo y se dividirá por la base, es decir, 8.
• Paso 4: El resto obtenido pasará a ser el segundo dígito menos significativo, es decir, se sumará a la izquierda del dígito obtenido anteriormente.

Ahora, se repiten los pasos 3 y 4 hasta que el cociente obtenido sea 0, y se suman a la izquierda de los dígitos existentes los residuos obtenidos tras cada iteración. 

C. Conversión de decimal a hexadecimal:

Los números hexadecimales se representan en base 16. Por lo tanto, para convertir un número decimal a un número hexadecimal, se debe cambiar la base de ese número. Siga los pasos que se indican a continuación:

• Paso 1: divide el número decimal con la base del sistema numérico al que se convertirá. Aquí la conversión es hexadecimal, por lo que el divisor será 16. 
• Paso 2: El resto obtenido de la división se convertirá en el dígito menos significativo del nuevo número.
• Paso 3: El cociente obtenido de la división se convertirá en el siguiente dividendo y se dividirá por la base, es decir, 16.
• Paso 4: El resto obtenido pasará a ser el segundo dígito menos significativo, es decir, se sumará a la izquierda del dígito obtenido anteriormente.

Ahora, se repiten los pasos 3 y 4 hasta que el cociente obtenido sea 0, y se suman a la izquierda de los dígitos existentes los residuos obtenidos tras cada iteración. 

2. Conversión del sistema numérico binario a otros sistemas numéricos

Los números binarios se representan con los dígitos 0 y 1 y con base 2. La conversión de un sistema numérico significa la conversión de una base a otra. Los siguientes son la conversión del sistema numérico binario a otros sistemas numéricos:

A. Conversión de binario a decimal: 

Los números binarios se representan en base 2 pero los números decimales son de base 10. Por lo tanto, para convertir el número binario en un número decimal, se debe cambiar la base de ese número. Siga los pasos que se indican a continuación:

• Paso 1: Multiplique cada dígito del número binario con el valor posicional de ese dígito, comenzando de derecha a izquierda, es decir, de LSB a MSB. 
• Paso 2: Sume el resultado de esta multiplicación y se formará el número decimal.

Ejemplo: convertir (11101011) ₂ en un número decimal

B. Conversión de binario a octal:

Los números binarios se representan en base 2 pero los números octales son de base 8. Por lo tanto, para convertir el número binario en número octal, se debe cambiar la base de ese número. Siga los pasos que se indican a continuación:

• Paso 1: Divida el número binario en grupos de tres dígitos comenzando de derecha a izquierda, es decir, de LSB a MSB.
• Paso 2: Convierta estos grupos en dígitos octales equivalentes.

Ejemplo: convertir (11101011) ₂ en un número octal

C. Conversión de binario a hexadecimal:

Los números binarios se representan en base 2, pero los números hexadecimales son de base 10. Por lo tanto, para convertir el número binario en número hexadecimal, se debe cambiar la base de ese número. Siga los pasos que se indican a continuación:

• Paso 1: Divida el número binario en grupos de cuatro dígitos comenzando de derecha a izquierda, es decir, de LSB a MSB.
• Paso 2: Convierta estos grupos en dígitos hexadecimales equivalentes.

Ejemplo: Para convertir (1110101101101) ₂ en un número hexadecimal

 

3. Conversión del sistema numérico octal a otros sistemas numéricos

Los números octales se representan con los dígitos 0-7 y con base 8. La conversión de un sistema numérico significa la conversión de una base a otra. Las siguientes son las conversiones del sistema numérico octal a otros sistemas numéricos:

A. Conversión de octal a decimal: 

Los números octales se representan en base 8, pero los números decimales son de base 10. Por lo tanto, para convertir un número octal en un número decimal, se debe cambiar la base de ese número. Siga los pasos que se indican a continuación:

• Paso 1: Multiplique cada dígito del número octal con el valor posicional de ese dígito, comenzando de derecha a izquierda, es decir, de LSB a MSB.
• Paso 2: Sume el resultado de esta multiplicación y se formará el número decimal.

Ejemplo: 

B. Conversión octal a binaria:

Los números octales se representan en base 8, pero los números binarios son de base 2. Por lo tanto, para convertir un número octal en un número binario, se debe cambiar la base de ese número. Siga los pasos que se indican a continuación:

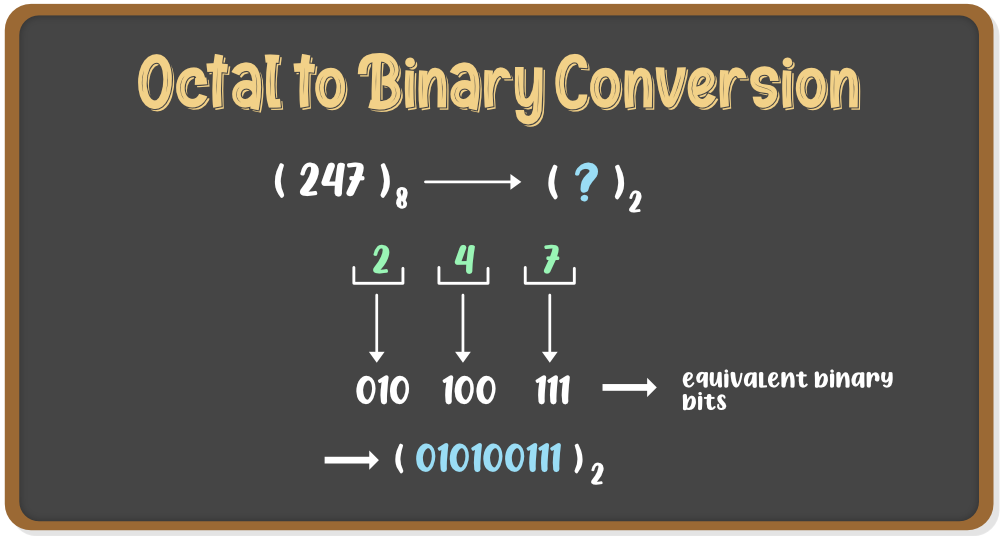
• Paso 1: Escribe cada dígito del número octal por separado.
• Paso 2: Convierta cada dígito en un grupo equivalente de tres dígitos binarios.
• Paso 3: Combina estos grupos para formar el número binario completo.

Ejemplo: (247) ₈ se va a convertir a binario

C. Conversión octal a hexadecimal:

Los números octales se representan en base 8, pero los números hexadecimales son de base 16. Por lo tanto, para convertir un número octal en un número hexadecimal, se debe cambiar la base de ese número. Siga los pasos que se indican a continuación:

• Paso 1: primero necesitamos convertir el número octal a binario. Para eso, siga los pasos dados en la conversión anterior.
• Paso 2: Ahora, para convertir el número binario a número hexadecimal, divida los dígitos binarios en grupos de cuatro dígitos comenzando de derecha a izquierda, es decir, de LSB a MSB. 
• Paso 3: agregue ceros antes de MSB para convertirlo en un grupo adecuado de cuatro dígitos (si es necesario)
• Paso 4: Ahora convierta estos grupos en sus valores decimales relevantes.
• Paso 5: para valores de 10 a 15, conviértalos en símbolos hexadecimales, es decir, de AF

Ejemplo: (5456) ₈ se va a convertir a hexadecimal

4. Conversión del sistema numérico hexadecimal a otros sistemas numéricos

Los números hexadecimales se representan con dígitos del 0 al 9 y con letras AF y con base 16. La conversión de un sistema numérico significa la conversión de una base a otra. Las siguientes son las conversiones del sistema numérico hexadecimal a otros sistemas numéricos:

A. Conversión de hexadecimal a decimal: 

Los números hexadecimales se representan en base 16, pero los números decimales son de base 10. Por lo tanto, para convertir un número hexadecimal en un número decimal, se debe cambiar la base de ese número. Siga los pasos que se indican a continuación:

• Paso 1: escriba los valores decimales de los símbolos utilizados en el número hexadecimal, es decir, de AF
• Paso 2: Multiplica cada dígito del número hexadecimal por su valor posicional. comenzando de derecha a izquierda, es decir, LSB a MSB.
• Paso 3: suma el resultado de las multiplicaciones y la suma final será el número decimal.

Ejemplo: Para convertir (8EB4) ₁₆ en un valor decimal

B. Conversión de hexadecimal a binario:

Los números hexadecimales se representan en base 16, pero los números binarios son de base 2. Por lo tanto, para convertir un número hexadecimal en un número binario, se debe cambiar la base de ese número. Siga los pasos que se indican a continuación:

• Paso 1: Convierta los símbolos hexadecimales en sus valores decimales equivalentes.
• Paso 2: Escriba cada dígito del número hexadecimal por separado.
• Paso 3: Convierta cada dígito en un grupo equivalente de cuatro dígitos binarios.
• Paso 4: Combina estos grupos para formar el número binario completo.

Ejemplo: (B2E) ₁₆ se va a convertir a binario

C. Conversión hexadecimal a octal:

Los números hexadecimales se representan en base 16, pero los números octales son de base 8. Por lo tanto, para convertir un número hexadecimal en un número octal, se debe cambiar la base de ese número. Siga los pasos que se indican a continuación:

• Paso 1: primero necesitamos convertir el número hexadecimal a binario. Para eso, siga los pasos dados en la conversión anterior.
• Paso 2: Ahora, para convertir el número binario a número octal, divida los dígitos binarios en grupos de tres dígitos comenzando de derecha a izquierda, es decir, de LSB a MSB. 
• Paso 3: agregue ceros antes de MSB para que sea un grupo adecuado de tres dígitos (si es necesario)
• Paso 4: Ahora convierta estos grupos en sus valores decimales relevantes.

Ejemplo: (B2E) ₁₆ se va a convertir a hexadecimal