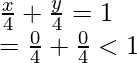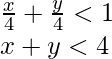Solución Gráfica de Desigualdades Lineales en Dos Variables

posee

¿Qué son las Desigualdades?

Consideremos un ejemplo, Anil quiere comprar algunas bebidas frías. Cada bebida fría cuesta 20 rupias y tiene un total de 190 rupias con él. Supongamos que compra x bebidas frías. ¿Cuál puede ser el valor máximo de x? Se puede representar en forma de una ecuación dada a continuación, 

20x <190

Dos expresiones reales o números reales relacionados por los símbolos “<“, “>”, “≤” o “≥” se denominan desigualdades. El enunciado anterior es una desigualdad. Hay dos tipos de desigualdades: 

1. Desigualdades numéricas: 3 < 5 o 7 > 5.
2. Desigualdades Literales: x > 5 y y < 7.

Algunos ejemplos generales de las desigualdades son, 

hacha + por + c > 0 ….(1)

hacha + por + c < 0 ….(2) 

hacha + por + c ≥ 0 ….(3)

hacha + por + c ≤ 0 ….(4)

De las ecuaciones anteriores, las ecuaciones (1) y (2) se denominan desigualdades estrictas, y (3) y (4) se denominan desigualdades de holgura. 

Soluciones de Desigualdades

Cualquier solución a una desigualdad es el valor de esa variable que hace que la desigualdad sea un enunciado verdadero. Por ejemplo, supongamos que tenemos una desigualdad x < 5. En tal caso, todos los valores de x menores que 5 hacen de esta desigualdad una verdadera desigualdad. Al resolver desigualdades, debemos tener en cuenta algunas reglas, 

1. Se pueden sumar o restar números iguales de ambos lados de la desigualdad.
2. Ambos lados de una desigualdad se pueden multiplicar (o dividir) por el mismo número positivo. Pero cuando ambos lados se multiplican o dividen por un número negativo, entonces se invierte el signo de la desigualdad.

Estas operaciones no afectan la desigualdad y pueden usarse para simplificarnos la desigualdad. 

Pregunta: Resuelva la desigualdad 20x < 80 y muestre sus soluciones en un gráfico. 

Solución: 

Se nos da, 

20x <80

Sabemos que dividir la desigualdad por un número positivo no cambia nada. Dividamos la desigualdad por 20. 

X < 4. 

Ahora todos los valores menores a 10 son soluciones a esta desigualdad. La siguiente figura representa esta solución en el gráfico. 

Representaciones gráficas de desigualdades en dos variables 

Vimos la gráfica de una desigualdad lineal en una variable. Una ecuación lineal en dos variables representa una línea que divide el plano en dos partes. Llamamos a cada parte semiplano. Si la línea es vertical, dividirá el plano en el semiplano izquierdo y el semiplano derecho y la línea no vertical dividirá el plano en el semiplano superior izquierdo y el semiplano inferior. 

Cualquier punto en el plano cartesiano estará en la línea o en cualquiera de los semiplanos I y II. 

Digamos que tenemos una línea, 

hacha + por = c

Aquí, a ≠ 0 y b ≠ 0. 

Ahora cuando ponemos cualquier punto (x, y) en la ecuación, hay tres casos posibles: 

1. hacha + por > c
2. hacha + por < c
3. hacha + por = c

Veamos todos los casos

Caso (i): ax + by > c

Digamos b > 0. Considere un punto (h, k) que satisface la ecuación. Después, 

ah + bk = c

Tomando otro punto arbitrario (h, l). La siguiente figura representa los dos puntos junto con la línea. Sabemos, 

l > k 

bl > bk 

ah + bl > ah +bk 

ah + bl > c

Así, el punto (h, l) satisface la propiedad ax + by > c. Por lo tanto, todos los puntos que se encuentran en el semiplano II satisfacen esta desigualdad. Para b < 0 también, esto se puede demostrar de manera similar. 

Caso (ii): ax + by = c

Todos los puntos que satisfacen la línea, que está sobre la línea, satisfacen esta ecuación.

Caso (iii): ax + por < c 

Todos los puntos restantes, es decir, los puntos que se encuentran en el semiplano, satisfago esta desigualdad. 

Veamos algunos problemas con estos conceptos. 

Problemas de muestra 

Pregunta 1: Resuelve la ecuación 5x + 3y > 6 gráficamente. 

Solución: 

Primero, necesitamos dibujar la gráfica para 5x + 3y = 6. Se puede hacer trayendo la ecuación en forma de intersección de pendiente o en forma de intersección. 

Ahora seleccione un punto arbitrariamente para verificar. Tomemos (0,0). 

Sustituyendo este punto (0,0) en la ecuación, 

5(0) + 3(0) = 0 < 6. 

Por lo tanto, los puntos en la mitad inferior satisfarán 5x + 3y < 6. Por lo tanto, todos los puntos que satisfagan la ecuación dada estarán en el semiplano superior. 

Pregunta 2: Resuelva la ecuación 6x + 2y > 3 gráficamente. 

Solución: 

Primero, necesitamos dibujar el gráfico para 6x + 2y = 3. Se puede hacer trayendo la ecuación en forma de intersección de pendiente o en forma de intersección. 

Poniendo (0,0) en la ecuación, 

6(0) + 2(0) = 0 < 3. Así, los puntos en el semiplano superior satisfacen la ecuación dada. 

6x + 2y > 3

Pregunta 3: Resuelva la ecuación x + y < 2 gráficamente. 

Solución: 

La ecuación dada es, x + y < 2. 

Poniendo el (0, 0) en la ecuación, 

0 < 2. 

Este punto satisface la ecuación dada. Por lo tanto, el gráfico será, 

Pregunta 4: Resuelve la ecuación 3x – 5y < 20 gráficamente. 

Solución: 

Como de costumbre, tomaremos (0, 0) como el punto en el que queremos probar. 

3(0) – 5(0) < 20. 

Este punto satisface la desigualdad dada. Por lo tanto, el semiplano superior izquierdo satisface la desigualdad. 

Pregunta 5: Forma la desigualdad a partir del gráfico que se muestra a continuación. 

Solución: 

Podemos ver que esta línea es paralela a uno de los ejes. La ecuación de la recta es, 

x = 4

Ahora queremos formar la desigualdad lineal para la región sombreada. (0,0) en la región sombreada, así que lo comprobaremos. 

x = 0 < 4 

Por lo tanto, la región sombreada satisface, 

X < 4

Pregunta 6: Forme la desigualdad a partir del gráfico que se muestra a continuación. 

Solución: 

Del gráfico, primero deduzcamos la ecuación de la línea. Podemos ver que las intersecciones de los ejes x e y tienen una longitud de 4. 

Ahora tenemos que averiguar qué condición cumple el semiplano inferior. Usemos (0,0) ya que pertenece al semiplano inferior. Sustituyendo el valor (0,0) en la ecuación, 

Asi que,