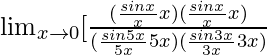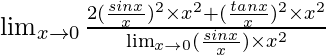Pregunta 1. Lim x→0 [sen3x/5x]
Solución:
Tenemos,
Lím x→0 [sen3x/5x]
= (1/5)Lím x→0 [sen3x/3x] × 3
= (3/5)Lím x→0 [sen3x/3x]
Como sabemos, Lim x→0 [senx/x] = 1
= (3/5)
Pregunta 2. Lim x→0 [senx°/x]
Solución:
Tenemos,
Lim x→0 [senx°/x]
Como sabemos que x° = [(πx)/180]
= Lim x→0 [sin{(πx)/180}/x]
=
= (π/180) × 1
= (π/180)
Pregunta 3. Lim x→0 [x 2 /senx 2 ]
Solución:
Tenemos,
Lim x→0 [x 2 /senx 2 ]
=
=
Como sabemos, Lim x→0 [senx/x] = 1
= 1/1
= 1
Pregunta 4. Lim x→0 [sinx.cosx/3x]
Solución:
Tenemos,
Lim x→0 [(senx.cosx)/3x]
= Lim x→0 [(senx.cosx)/ × 3x]
= 1/3 Lim x→0 [(senx)/x] × Lim x→0 [(cosx)]
Como sabemos que Lim x→0 [senx/x] = 1, y Lim x→0 cos0 = 1
= (1/3) × 1 × 1
= 1/3
Pregunta 5. Lim x→0 [(3senx – 4sen 3 x)/x]
Solución:
Tenemos,
Lim x→0 [(3senx – 4sen 3x )/x]
Como sabemos que 3senx – 4sen 3 x = sen3x
= Lim x→0 [(sen3x)/3x] × 3
= 3 × Lim x→0 [(sen3x)/3x]
Como sabemos, Lim x→0 [senx/x] = 1
= 3 × 1
= 3
Pregunta 6. Lim x→0 [tan8x/sin2x]
Solución:
Tenemos,
Límite x→0 [tan8x/sen2x]
=
=
Como sabemos que Lim x→0 [sin2x/2x] = 1 y Lim x→0 [tan8x/8x] = 1
= 8/2
= 4
Pregunta 7. Lim x→0 [tan(mx)/tan(nx)]
Solución:
Tenemos,
Lim x→0 [tan(mx)/tan(nx)]
=
=
Como sabemos que Lim x→0 [tanx/x] = 1
= metro × 1/n × 1
= m/n
Pregunta 8. Lim x→0 [sin5x/tan3x]
Solución:
Tenemos,
Límite x→0 [sen5x/tan3x]
=
=
Como sabemos que Lim x→0 [sin5x/5x] = 1 y Lim x→0 [tan3x/3x] = 1
= 5/3 × 1
= 5/3
Pregunta 9. Lim x→0 [sen(x n )/(x n )]
Solución:
Tenemos,
Lim x→0 [sen(x n )/(x n )]
es en forma de 0/0
Entonces, sea x n = y
x→0 que y→0
Lim y→0 [seny/y]
Como sabemos que Lim y→0 [seny/y] = 1
= 1
Pregunta 10. Lim x→0 [(7xcosx – 3senx)/(4x + tanx)]
Solución:
Tenemos,
Lim x→0 [(7xcosx – 3senx)/(4x + tanx)]
= Lim x→0 [x(7cosx-3senx/x)/x(4 + tanx/x)]
= Lim x→0 [(7cosx-3senx/x)/(4 + tanx/x)]
=
Como sabemos que Lim x→0 [senx/x] = 1 y Lim x→0 [tanx/x] = 1
= (7 – 3)/(4 + 1)
= 4/5
Pregunta 11. Lim x→0 [{cos(ax) – cos(bx)}/{cos(cx) – cos(dx)}]
Solución:
Tenemos,
Lim x→0 [{cos(ax) – cos(bx)}/{cos(cx) – cos(dx)}]
=
=
=
=
= (a 2 – b 2 )/(c 2 – d 2 )
Pregunta 12. Lim x→0 [(tan 2 3x)/x 2 ]
Solución:
Tenemos,
Lim x→0 [(tan 2 3x)/x 2 ]
= Lim x→0 [(tan3x)/x] 2
= Lim x→0 [(tan3x)/3x] 2 × 9
Como sabemos que Lim x→0 [tanx/x] = 1
= 1 × 9
= 9
Pregunta 13. Lim x→0 [(1 – cosmx)/x 2 ]
Solución:
Tenemos,
Lim x→0 [(1 – cosmx)/x 2 ]
=
=
=
Como sabemos que Lim x→0 [senx/x] = 1
= 2 × (m/2) 2
= metro 2 /2
Pregunta 14. Lim x→0 [(3sin2x + 2x)/(3x + 2tan3x)]
Solución:
Tenemos,
Lim x→0 [(3sin2x + 2x)/(3x + 2tan3x)]
= Lim x→0 [2x(1 + 3sen2x/2x)/3 x (1 + 2tan3x/3x)]
= (2/3)Lím x→0 [(1 + 3sen2x/2x)/3 x (1 + 2tan3x/3x)]
=
Como sabemos que Lim x→0 [senx/x] = 1 y Lim x→0 [tanx/x] = 1
= (2/3) × (4/3)
= 8/9
Pregunta 15. Lim x→0 [(cos3x – cos7x)/x 2 ]
Solución:
Tenemos,
=
= Lim x→0 [-2sin5x.sin(-2x)/x 2 ]
= Lím x→0 [2sin5x.sen2x/x 2 ]
=
Como sabemos que Lim x→0 [senx/x] = 1
= 2 × 5 × 2
= 20
Pregunta 16. Lim θ→0 [sin3θ/tan2θ]
Solución:
Tenemos,
Lim θ→0 [sen3θ/tan2θ]
=
=
Como sabemos que Lim x→0 [senx/x] = 1 y Lim x→0 [tanx/x] = 1
= 3/2
Pregunta 17. Lim x→0 [senx 2 (1 – cosx 2 )/x 6 ]
Solución:
Tenemos,
Lim x→0 [senx 2 (1 – cosx 2 )/x 6 ]
= Lim x→0 [senx 2 {2sen(x 2 /2}/x 6 ]
=
=
=
Como sabemos que Lim x→0 [senx/x] = 1
= 2 × (1/4)
= 1/2
Pregunta 18. Lim x→0 [sen 2 (4x 2 )/x 4 ]
Solución:
Tenemos,
Lim x→0 [sen 2 (4x 2 )/x 4 ]
= Lim x→0 [(sen(4x 2 )) 2 /(x 2 ) 2 ]
= Lim x→0 [sen(4x 2 )/4x 2 ] 2 × 4 2
Como sabemos que Lim x→0 [senx/x] = 1
= 4 2
= 16
Pregunta 19. Lim x→0 [(xcosx + 2senx)/(x 2 + tanx)]
Solución:
Tenemos,
Lim x→0 [(xcosx + 2senx)/(x 2 + tanx)]
= Lim x→0 [x(cosx + 2senx/x)/x(x + tanx/x)]
= Lim x→0 [(cosx + 2senx/x)/(x + tanx/x)]
=
Como sabemos que Lim x→0 [senx/x] = 1 y Lim x→0 [tanx/x] = 1
= (1 + 2)/(0 + 1)
= 3
Pregunta 20. Lim x→0 [(2x – senx)/(x + tanx)]
Solución:
Tenemos,
Lim x→0 [(2x – senx)/(x + tanx)]
= Lim x→0 [x(2 – senx/x)/x(1 + tanx/x)]
= Lim x→0 [(2 – senx/x)/(1 + tanx/x)]
=
Como sabemos que Lim x→0 [senx/x] = 1 y Lim x→0 [tanx/x] = 1
= (2 – 1)/(1 + 1)
= 1/2
Pregunta 21. Lim x→0 [(5xcosx + 3senx)/(3x 2 + tanx)]
Solución:
Tenemos,
Lim x→0 [(5xcosx + 3senx)/(3x 2 + tanx)]
= Lim x→0 [x(5cosx + 3senx/x)/x(3x + tanx/x)]
= Lim x→0 [(5cosx + 3senx/x)/(3x + tanx/x)]
=
Como sabemos que Lim x→0 [senx/x] = 1 y Lim x→0 [tanx/x] = 1
= (5 cos0 + 3)/(0 + 1)
= 8
Pregunta 22. Lim x→0 [(sen3x – senx)/(senx)]
Solución:
Tenemos,
Lim x→0 [(sen3x – senx)/(senx)]
=
= 2Lím x→0 [cos2x.senx/senx]
= 2Lím x→0 cos2x
= 2 × cos0
= 2 × 1
= 2
Pregunta 23. Lim x→0 [(sen5x – sin3x)/(senx)]
Solución:
Tenemos,
Límite x→0 [(sen5x – sin3x)/(senx)]
=
= 2Lím x→0 [cos4x.senx/senx]
= 2Lím x→0 cos4x
= 2 × cos0
= 2 × 1
= 2
Pregunta 24. Lim x→0 [(cos3x – cos5x)/x 2 ]
Solución:
Tenemos,
Lim x→0 [(cos3x – cos5x)/x 2 ]
=
= Lim x→0 [-2sin4x.sin(-x)/x 2 ]
= Lim x→0 [2sin4x.senx/x 2 ]
=
Como sabemos que Lim x→0 [senx/x] = 1
= 2 × 4 × 1
= 8
Pregunta 25. Lim x→0 [(tan3x – 3x)/(3x – sen 2 x)]
Solución:
Tenemos,
Lim x→0 [(tan3x – 3x)/(3x – sen 2 x)]
= Lim x→0 [x(tan3x/x – 3)/x(3 – sen 2 x/x)]
= Lim x→0 [(tan3x/x – 3)/(3 – sen 2 x/x)]
=
Como sabemos que Lim x→0 [senx/x] = 1
= (3 – 2)/(3 – 0)
= 1/3
Pregunta 26. Lim x→0 [{sin(2 + x) – sin(2 – x)}/x]
Solución:
Tenemos,
Lim x→0 [{sen(2 + x) – sin(2 – x)}/x]
=
= 2Lím x→0 [cos2.senx/x]
= 2cos×2Lím x→0 [senx/x]
Como sabemos que Lim x→0 [senx/x] = 1
= 2cos2
Pregunta 27. Lim h→0 [{(a + h) 2 sin(a + h) – a 2 sina}/h]
Solución:
Tenemos,
Lim h→0 [{(a + h) 2 sin(a + h) – a 2 sina}/h]
= Lim h→0 [{a 2 sin(a + h) + h 2 sin(a + h) + 2ahsin(a + h) – a 2 sina}/h]
=
=
=
= a 2 cosa + 0 + 2 asina
= a 2 cosa + 2 asina
Pregunta 28. Lim x→0 [{tanx – senx}/{sen3x – 3senx}]
Solución:
Tenemos,
Lim x→0 [{tanx – senx}/{sen3x – 3senx}]
=
=
=
=
=
= (-1/4)(1/2)
= -(1/8)
Pregunta 29. Lim x→0 [{sex5x – sec5x}/{sec3x – secx}]
Solución:
Tenemos,
Lim x→0 [{sex5x – sec5x}/{sec3x – secx}]
=
=
=
=
=
Como sabemos que Lim x→0 [senx/x] = 1
= (4x/2x)(cos0/cos0)
= 2
Pregunta 30. Lim x→0 [{1 – cos2x}/{cos2x – cos3x}]
Solución:
Tenemos,
Lim x→0 [{1 – cos2x}/{cos2x – cos3x}]
=
=
=
=
Como sabemos que Lim x→0 [senx/x] = 1
= (1/5 × 3)
= 1/15
Pregunta 31. Lim x→0 [(1 – cos2x + tan 2 x)/(xsenx)]
Solución:
Tenemos,
Lim x→0 [(1 – cos2x + tan 2 x)/(xsenx)]
= Lim x→0 [(2sen 2 x + tan 2 x)/(xsenx)]
Dividiendo numerador y denominador por x 2
=
Como sabemos que Lim x→0 [senx/x] = 1 y Lim x→0 [tanx/x] = 1
= (2 × 1 × x 2 + 1) + (1 × x 2 ) /(1 × x 2 )
= 3
Publicación traducida automáticamente
Artículo escrito por vivekray59 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{-2sin(\frac{ax+bx}{2})sin(\frac{ax-bx}{2})}{-2sin(\frac{cx+dx}{2})sin(\frac{cx-dx}{2})}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-528b21a544687f5647e22c3fb02d7f87_l3.png)
![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{\frac{sin(\frac{ax+bx}{2})}{(\frac{ax+bx}{2})}×(\frac{ax+bx}{2})\frac{sin(\frac{ax-bx}{2})}{(\frac{ax-bx}{2})}×(\frac{ax-bx}{2})}{\frac{sin(\frac{cx+dx}{2})}{(\frac{cx+dx}{2})}×(\frac{cx+dx}{2})\frac{sin(\frac{cx-dx}{2})}{(\frac{cx-dx}{2})}×(\frac{cx-dx}{2})}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7251dec0699ffd24b5032194ba3a05af_l3.png)
![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{\frac{(ax+bx)}{2}\frac{(ax-bx)}{2}}{\frac{(cx+dx)}{2}\frac{(cx-dx)}{2}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-56cfc094221708a097d62962bd6531da_l3.png)

![Rendered by QuickLaTeX.com 2\lim_{x\to0}[\frac{sinx^2.sin^2(\frac{x^2}{2})}{x^6}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8b6e7ce010647b22bba7c979a707530d_l3.png)
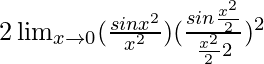
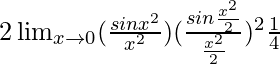
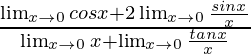
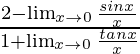

![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{\frac{tan3x}{3x}×3-2}{3-\frac{sinx}{x}×sinx}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f55a3177015759a92111248b900083bd_l3.png)
![Rendered by QuickLaTeX.com \lim_{h\to0}[a^2\frac{2cos\frac{(a+h+a)}{2}sin\frac{(a+h-a)}{2}}{2×\frac{h}{2}}+hsin(a+h)+2asin(a+h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fd5d962e38cc9c0b0e21144a86b0218b_l3.png)
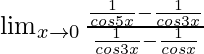
![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{\frac{sin4x}{4x}×4x}{\frac{sin2x}{2x}×2x}][\frac{cosx}{cos5x}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-da050c618dedf8b53cbe3d4d9d97785e_l3.png)