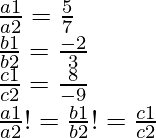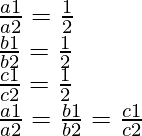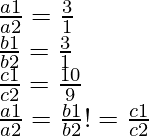Pregunta 1. Akhila fue a una feria en su pueblo. Quería disfrutar de los paseos en la Rueda Gigante y jugar Hoopla (un juego en el que arrojas un aparejo sobre los artículos en el puesto, y si el aro cubre cualquier objeto por completo, lo obtienes). El número de veces que jugó Hoopla es la mitad del número de paseos que tuvo en la rueda gigante. Cada viaje cuesta ₹ 3 y un juego de alboroto cuesta ₹ 4. Si gastó ₹ 20 en la feria, representa esta situación algebraica y gráficamente.
Solución:
Supongamos que el número de paseos en la rueda es x
Y número de juego de Hoopla para ser y.
Según las restricciones dadas,
x = 2y ⇒ x – 2y = 0 ….(yo)
Costo de paseo en rueda a razón de Rs. 3 = 3x
Costo en Hoopla = 4 años
Ahora, el costo total = Rs. 20
3x + 4y = 20 ….(ii)
Resolviendo las ecuaciones (i) y (ii), obtenemos,
Tomando al menos tres puntos de cada línea y conectándolos para formar una línea. El punto de intersección tiene la solución, en este caso.
De la ecuación (i)
x = 2y
X 0 4 6 y 0 2 3 De manera similar, en la ecuación (ii)
3x + 4y = 20 ⇒ 3x = 20 – 4y
Calculando los puntos para estas líneas,
X 4 0 8 y 2 5 -1 Trazando estos puntos y uniendo el punto de intersección, obtenemos el punto (4, 2)
La única solución es (4, 2).
Por lo tanto, obtenemos, x = 4, y = 2
Pregunta 2. Aftab le dice a su hija: “Hace siete años, yo tenía siete veces la edad que tenías tú entonces. Además, dentro de tres años tendré el triple de la edad que tú tendrás. ¿No es esto interesante? Representa esta situación de forma algebraica y gráfica.
Solución:
Hace siete años :
Supongamos que la edad de la hija de Aftab es x años.
Y, la edad de Aftab para ser y años.
Tres años despues,
Edad de la hija = x + 10 años
Edad de Aftab = y + 10 años
De acuerdo con las restricciones dadas,
y = 7x ⇒ 7x – y = 0 ……….(i)
y + 10 = 3 (x + 10)
=> y + 10 = 3x + 30
3x – y = 10 – 30 = -20
3x – y = -20 ….(ii)
Se obtienen las siguientes ecuaciones:
7x – y = 0
3 x – y = -20
Resolviendo estas ecuaciones lineales gráficamente:
7x – y = 0 ⇒ y = 7x
Trazando los puntos de la primera línea,
X 0 1 -1 y 0 7 -7 Para la segunda ecuación, obtenemos,
3x – y = -20
y = 3x + 20
Trazando los puntos de la segunda línea,
X -1 -2 -3 y 17 14 11 Trazando estos puntos y uniendo el punto de intersección, obtenemos el punto (5, 35).
Pregunta 3. La trayectoria del tren A viene dada por la ecuación 3x+4y-12 =0 y la trayectoria de otro tren B viene dada por la ecuación 6x+8y-48 =0. Representa gráficamente esta situación.
Solución:
Las restricciones dadas son:
La trayectoria de un tren es 3x + 4y – 12 = 0
y la trayectoria del tren B es 6x + 8y – 48 = 0
Cálculo de los puntos de la recta 3x + 4y- 12 = 0
X 4 0 -4 y 0 3 6 Además, trazar los puntos de la segunda ecuación 6x+8y-48 =0.
X 8 4 0 y 0 3 6 Trazando gráficamente estos puntos y uniendo el punto de intersección, obtenemos que el par de rectas son paralelas.
Pregunta 4. Gloria camina por el camino que une (-2, 3) y (2, -2), mientras que Suresh camina por el camino que une (0, 5) y (4, 0). Representa gráficamente esta situación.
Solución:
Graficamos los puntos (-2, 3) y (2, -2) y los conectamos para formar una línea.
Además, trazamos los puntos (0, 5), (4, 0) y los conectamos para obtener otra línea.
Gráficamente obtenemos que estas dos rectas son paralelas entre sí.
Pregunta 5. Al comparar las razones, y sin dibujarlas, averigua si las rectas que representan los siguientes pares de ecuaciones lineales se cortan en un punto, son paralelas o coinciden:
(yo) 5x – 4y + 8 = 0
7x + 6y – 9 = 0
(ii) 9x + 3y +12 = 0
18x + 6y + 24 = 0
(iii) 6x – 3y +10 = 0
2x – y + 9 = 0
Solución:
(i) Tenemos el siguiente par de ecuaciones,
5x – 4y + 8 = 0
7x + 6y – 9 = 0
Tenemos los siguientes coeficientes para estas ecuaciones,
a1 = 5, b1 = -4, c1= 8
Y, a2 = 7, b2= 6 y c2 = -9
Por lo tanto, estas dos líneas se cortan en un único punto.
(ii) Tenemos el siguiente par de ecuaciones,
9x + 3y +12 = 0
18x + 6y + 24 = 0
Tenemos los siguientes coeficientes para estas ecuaciones,
a1 = 9, b1 = 3, c1= 12
Y, a2 = 18, b2= 6 y c2 = 24
Por lo tanto, estas líneas son líneas coincidentes.
(iii) Tenemos el siguiente par de ecuaciones,
6x – 3y +10 = 0
2x – y + 9 = 0
Tenemos los siguientes coeficientes para estas ecuaciones,
a1 = 6, b1 = -3, c1= 10
Y, a2 = 2, b2= -1 y c2 = 9
Por lo tanto, estas líneas son paralelas.
Pregunta 6. Dada la ecuación lineal 2x + 3y – 8 = 0, escribe otra ecuación lineal en dos variables tal que la representación geométrica del par así formado sea:
(i) líneas que se cruzan
(ii) líneas paralelas
(iii) líneas coincidentes
Solución:
Tenemos la ecuación 2x+3y-8, ahora los coeficientes son a1 = 2 , b1= 3 y c1 = -8 respectivamente.
(i) Para un par de líneas que se intersecan, la razón de los coeficientes de la segunda ecuación no debe ser igual a los coeficientes correspondientes de la primera.
Entonces, tomemos a2 = 3, b2 = 4 y c2 = 2
es decir, la segunda ecuación es 3x+4y+2 = 0
(ii) Para líneas paralelas, tenemos,
a1/a2 = b1/b2 ≠ c1/c2
Por lo tanto, a2/b2 puede ser 2/3.
Tomemos a2 = 4 y b2 = 6,
es decir, la segunda ecuación es 4x+6y+5 = 0
(iii) Para líneas coincidentes, tenemos,
a1/a2 = b1/b2 = c1/c2
es decir, la segunda ecuación es 4x+6y – 16 = 0
Pregunta 7. Se encontró que el costo de 2 kg de manzanas y 1 kg de uvas en un día era de Rs. 160. Después de un mes, el costo de 4 kg de manzanas y 2 kg de uvas es Rs. 300. Representa la situación de forma algebraica y geométrica.
Solución:
Supongamos que el costo de 1 kg de manzanas es Rs. X
Y, el costo de 1 kg de uvas a Rs. y
Ahora, de acuerdo con las restricciones dadas, obtenemos el siguiente conjunto de ecuaciones:
2x + y = 160
4x + 2y = 300
Ahora 2x + y = 160
y = 160 – 2x
Obtención de los puntos para esta línea:
X 20 40 60 y 120 80 40 La segunda ecuación, es 4x + 2y = 300
=> 2x + y = 150
=> y = 150 – 2x
Obtención de los puntos para esta línea:
X 40 50 60 y 70 50 30 Gráficamente obtenemos que estas dos rectas son paralelas entre sí.
Publicación traducida automáticamente
Artículo escrito por yashkumar0457 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA