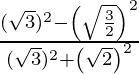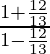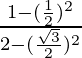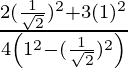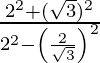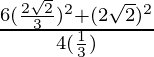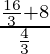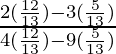Pregunta 1. Si cos θ = 4/5, encuentre todas las demás razones trigonométricas del ángulo θ .
Solución:
Nos dan, cos θ = 4/5. Entonces, sec θ =1/cos θ = 5/4.
Ahora sabemos,
=> sen θ = √(1 – cos 2 θ)
=> sen θ = √(1 – (4/5) 2 )
=> sen θ = √(1 – (16/25))
=> sen θ = √(9/25)
=> sen θ = 3/5
Entonces, cosec θ = 1/sen θ = 5/3
Y tan θ = sen θ/cos θ = (3/5)/(4/5) = 3/4
Por lo tanto, cot θ = 1/tan θ = 4/3
Si cos θ = 4/5, el valor de sec θ, sen θ, cosec θ, tan θ y cot θ son 5/4, 3/5, 5/3, 3/4 y 4/3 respectivamente.
Pregunta 2. Si sen θ = 1/√2, encuentre todas las demás razones trigonométricas del ángulo θ.
Solución:
Nos dan, sin θ = 1/√2. Entonces, cosec θ =1/sen θ = √2.
Ahora sabemos,
=> cos θ = √(1 – sen 2 θ)
=> porque θ = √(1 – (1/√2) 2 )
=> porque θ = √(1 – (1/2))
=> porque θ = √(1/2)
=> cos θ = 1/√2
Entonces, sec θ = 1/cos θ = √2
Y tan θ = sen θ/cos θ = (1/√2)/(1/√2) = 1
Por lo tanto, cot θ = 1/tan θ = 1
Si sen θ = 1/√2, el valor de cosec θ, cos θ, sec θ, tan θ y cot θ son √2, 1/√2, √2, 1 y 1 respectivamente.
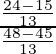
Pregunta 3. Si tan θ = 1/√2, encuentre el valor de 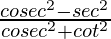 .
.
Solución:
Nos dan, tan θ = 1/√2. Ahora sabemos,
=> segundo θ = √(1 + tan 2 θ)
=> segundo θ = √(1 + (1/√2) 2 )
=> segundo θ = √(1+(1/2))
=> segundo θ = √(3/2)
Y cot θ = 1/tan θ = √2. También, sabemos,
=> cosec θ = √(1 + cuna 2 θ)
=> cosec θ = √(1 + (√2) 2 )
=> cosec θ = √(1 + 2)
=> cosec θ = √3
Entonces,
=
=
=
Por lo tanto, el valor de
es
.
Pregunta 4. Si tan θ = 3/4, encuentra el valor de 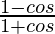 .
.
Solución:
Nos dan, tan θ = 3/4. Ahora sabemos,
=> segundo θ = √(1 + tan 2 θ)
=> segundo θ = √(1 + (3/4) 2 )
=> segundo θ = √(1+(9/16))
=> segundo θ = √(25/16)
=> segundo θ = 5/4
Y cos θ = 1/s θ = 4/5.
Entonces,
=
=
=
Por lo tanto, el valor de
es
.
Pregunta 5. Si tan θ = 12/5, encuentre el valor de 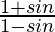 .
.
Solución:
Nos dan, tan θ = 12/5. Entonces, cot θ = 1/tan θ = 5/12.
Ahora sabemos,
=> cosec θ = √(1 + cuna 2 θ)
=> cosec θ = √(1 + (5/12) 2 )
=> cosec θ = √(1 + (25/144))
=> cosec θ = √(169/144)
=> cosec θ = 13/12
Y sen θ = 1/coseg θ = 12/13.
Entonces,
=
=
= 25
Por lo tanto, el valor de
es 25.
Pregunta 6. Si cot θ = 1/√3, encuentra el valor de 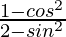 .
.
Solución:
Nos dan, cot θ = 1/√3. Ahora sabemos,
=> cosec θ = √(1 + cuna 2 θ)
=> cosec θ = √(1 + (1/√3) 2 )
=> cosec θ = √(1 + (1/3))
=> cosec θ = √(4/3)
=> cosec θ = 2/√3
Y sen θ = 1/coseg θ = √3/2. También, sabemos,
=> cos θ = √(1 – sen 2 θ)
=> porque θ = √(1 – (√3/2) 2 )
=> porque θ = √(1 – (3/4))
=> porque θ = √(1/4)
=> cos θ = 1/2
Entonces,
=
=
=
=
Por lo tanto, el valor de
es
.
Pregunta 7. Si cosec A = √2, encuentra el valor de 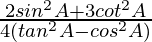 .
.
Solución:
Nos dan, cosec A = √2. Entonces, sen A = 1/coseg A = 1/√2.
Ahora sabemos,
=> cos A = √(1 – sen 2 A)
=> porque A = √(1 – (1/√2) 2 )
=> porque A = √(1 – (1/2))
=> porque A = √(1/2)
=> cos A = 1/√2
Por lo tanto, tan A = sin A/cos A = (1/√2)/(1/√2) = 1. Y cot A = 1/tan A = 1.
Entonces,
=
=
= 2
Por lo tanto, el valor de
es 2.
Pregunta 8. Si cot θ = √3, encuentra el valor de 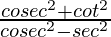 .
.
Solución:
Nos dan cot θ = √3. Y tan θ = 1/cot θ = 1/√3.
Ahora sabemos,
=> cosec θ = √(1 + cuna 2 θ)
=> cosec θ = √(1 + (√3) 2 )
=> cosec θ = √4
=> cosec θ = 2
También, sabemos,
=> segundo θ = √(1 + tan 2 θ)
=> segundo θ = √(1 + (1/√3) 2 )
=> segundo θ = √(1+(1/3))
=> segundo θ = √(4/3)
=> segundo θ = 2/√3
Entonces,
=
=
=
Por lo tanto, el valor de
es
.
Pregunta 9. Si 3cos θ = 1, encuentra el valor de 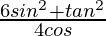 .
.
Solución:
Nos dan cos θ = 1/3. Ahora sabemos,
=> sen θ = √(1 – cos 2 θ)
=> sen θ = √(1 – (1/3) 2 )
=> sen θ = √(1 – (1/9))
=> sen θ = √(8/9)
=> sen θ = 2√2/3
Por lo tanto, tan θ = sen θ/cos θ = (2√2/3)/(1/3) = 2√2
Entonces,
=
=
=
= 10
Por lo tanto, el valor de
es 10.
Pregunta 10. Si √3 tan θ = sen θ, encuentra el valor de sen 2 θ – cos 2 θ.
Solución:
Nos dan, √3 tan θ = sin θ
=> √3 (sen θ/cos θ) = sen θ
=> cos θ = 1/√3
Ahora sabemos,
=> sen θ = √(1 – cos 2 θ)
=> sen θ = √(1 – (1/√3) 2 )
=> sen θ = √(1 – (1/3))
=> sen θ = √(2/3)
Entonces, sen 2 θ – cos 2 θ = √(2/3) 2 – (1/√3) 2
= 2/3 – 1/3
= 1/3
Por lo tanto, el valor de sen 2 θ – cos 2 θ es 1/3.
Pregunta 11. Si cosec θ = 13/12, encuentre el valor de 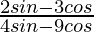 .
.
Solución:
Nos dan, cosec θ = 13/12. Entonces, sen θ = 1/coseg θ = 12/13.
Ahora sabemos,
=> cos θ = √(1 – sen 2 θ)
=> porque θ = √(1 – (12/13) 2 )
=> porque θ = √(1 – (144/169))
=> cos θ = √(25/169)
=> cos θ = 5/13
Entonces,
=
=
=
= 3
Por lo tanto, el valor de
es 3.
Pregunta 12. Si sen θ + cos θ = √2 cos (90 o –θ), encuentre cot θ.
Solución:
Se nos da,
=> sen θ + cos θ = √2 cos (90 o –θ)
=> sen θ + cos θ = √2 sen θ
=> cos θ = (√2–1)sen θ
=> cos θ/sen θ = √2–1
=> cuna θ = √2–1
Por lo tanto, el valor de cot θ es √2–1.
Pregunta 13. Si 2sen 2 θ – cos 2 θ = 2, entonces encuentra el valor de θ.
Solución:
Tenemos,
=> 2sen 2 θ – cos 2 θ = 2
=> 2sen 2 θ – (1 – sen 2 θ) = 2
=> 2sen 2 θ – 1 + sen 2 θ = 2
=> 3sen 2 θ = 3
=> sen 2 θ = 1
=> sen θ = 1
=> θ = 90 o
Por lo tanto, el valor de θ es 90 o .
Pregunta 14. Si √3tan θ – 1 = 0, encuentra el valor de sen 2 θ – cos 2 θ.
Solución:
Se nos da,
=> √3tan θ – 1 = 0
=> bronceado θ = 1/√3
=> tan θ = tan 30 o
=> θ = 30 o
Entonces, sen 2 θ – cos 2 θ = sen 2 30 o – cos 2 30 o
= (1/2) 2 – (√3/2) 2
= (1/4) – (3/4)
= –2/4
= –1/2
Por lo tanto, el valor de sen 2 θ – cos 2 θ es –1/2.
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA