Pregunta 1. Dibuja una ojiva por menos del método para los siguientes datos:
| Número de habitaciones | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Nº de casas | 4 | 9 | 22 | 28 | 24 | 12 | 8 | 6 | 5 | 2 |
Solución:
Número de habitaciones Nº de casas Frecuencia acumulada Menor o igual a 1 4 4 Menor o igual a 2 9 13 Menor o igual a 3 22 35 Menor o igual a 4 28 63 Menor o igual a 5 24 87 Menor o igual a 6 12 99 Menor o igual a 7 8 107 Menor o igual a 8 6 113 Menor o igual a 9 5 118 Menor o igual a 10 2 120 Graficamos los puntos (1, 4), (2, 13), (3, 35), (4, 63), (5, 87), (6, 99), (7, 107), (8, 113) ), (9, 118), (10, 120) respectivamente tomando el límite de clase superior sobre el eje x y la frecuencia acumulada sobre el eje y del gráfico.
Pregunta 2. Las calificaciones obtenidas por 750 estudiantes en un examen se dan en forma de una tabla de distribución de frecuencias:
| Marcas | Nº de Estudiantes |
| 600 – 640 | dieciséis |
| 640 – 680 | 45 |
| 680 – 720 | 156 |
| 720 – 760 | 284 |
| 760 – 800 | 172 |
| 800 – 840 | 59 |
| 840 – 880 | 18 |
Prepare una tabla de distribución de frecuencias acumuladas por el método menor que y dibuje una ojiva.
Solución:
Marcas Nº de Estudiantes marcas menos de Frecuencia acumulada 600 – 640 dieciséis 640 dieciséis 640 – 680 45 680 61 680 – 720 156 720 217 720 – 760 284 760 501 760 – 800 172 800 673 800 – 840 59 840 732 840 – 880 18 880 750
Pregunta 3. Dibuja una ojiva para representar la siguiente distribución de frecuencias:
| Intervalo de clases | 0 – 4 | 5 – 9 | 10 – 14 | 15 – 19 | 20 – 24 |
| Nº de alumnos | 2 | 6 | 10 | 5 | 3 |
Solución:
Convirtiendo la distribución de frecuencia dada en una distribución de frecuencia continua:
Intervalo de clases Nº de Estudiantes Menos que Frecuencia acumulada 0.5 – 4.5 2 4.5 2 4.5 – 9.5 6 9.5 8 9.5 – 14.5 10 14.5 18 14,5 – 19,5 5 19.5 23 19,5 – 24,5 3 24.5 26 Trazamos los puntos especificados (4.5, 2), (9.5, 8), (14.5, 18), (19.5, 23), (24.5, 26) en un gráfico tomando el límite de clase superior sobre el eje x y acumulando frecuencia sobre el eje y respectivamente.
Pregunta 4. Las ganancias mensuales (en Rs) de 100 tiendas se distribuyen de la siguiente manera:
| Beneficio por tienda | Nº de tiendas: |
| 0 – 50 | 12 |
| 50 – 100 | 18 |
| 100 – 150 | 27 |
| 150 – 200 | 20 |
| 200 – 250 | 17 |
| 250 – 300 | 6 |
Dibuja el polígono de frecuencia para ello.
Solución:
Ahora, calculando los siguientes datos, tenemos,
Beneficio por tienda Valor medio Nº de tiendas: menos de 0 0 0 Menos de 0 – 50 25 12 Menos de 50 – 100 75 18 Menos de 100 – 150 125 27 Menos de 150 – 200 175 20 Menos de 200 – 250 225 17 Menos de 250 – 300 275 6 Por encima de 300 300 0 Ahora, el polígono de frecuencia se puede calcular de la siguiente manera:
Pregunta 5. La siguiente distribución da el ingreso diario de 50 trabajadores de una fábrica:
| Ingreso diario (en Rs): | Nº de trabajadores: |
| 100 – 120 | 12 |
| 120 – 140 | 14 |
| 140 – 160 | 8 |
| 160 – 180 | 6 |
| 180 – 200 | 10 |
Convierta la distribución anterior en una distribución de frecuencia acumulada de tipo ‘menor que’ y dibuje su ojiva.
Solución:
Usando el método menor que, la siguiente distribución se puede convertir en una distribución continua, como,
Ingreso diario Frecuencia acumulada Menos de 120 12 Menos de 140 26 Menos de 160 34 Menos de 180 40 menos de 200 50 Marque el punto (120, 12), (140, 26), (160, 34), (180, 40), (200, 50), tomando el límite de clase superior en el eje x y las frecuencias acumuladas en el eje y respectivamente .
Pregunta 6. La siguiente tabla da el rendimiento de producción por hectárea de trigo de 100 fincas de un pueblo:
| Rendimiento de producción | 50-55 | 55-60 | 60-65 | 65-70 | 70-75 | 75-80 en kg por hectárea |
| Número de fincas | 2 | 8 | 12 | 24 | 38 | dieciséis |
Dibuje la ojiva ‘menor que’ y la ojiva ‘más que’.
Solución:
(i) Cálculo de la ojiva menor que
Rendimiento de producción
en kg 1 hectárea
Clase Nº de fincas.
(F)
cf menos de 55 50-55 2 2 menos de 60 55-60 8 10 menos de 65 60-65 12 22 menos de 70 65-70 24 46 menos de 75 70-75 38 84 menos de 80 75-80 dieciséis 100 Trazamos los puntos especificados (55, 2), (60, 10), (65, 22), (70, 46), (75, 84) y (80, 100) y los conectamos para formar una ojiva.
(ii) Más de
Rendimiento de producción cf Clase Mayor o igual a 50 100 50-55 Mayor o igual a 55 84 55-60 Mayor o igual a 60 46 60-65 Mayor o igual a 65 22 65-70 Mayor o igual a 70 10 70-75 Mayor o igual a 75 2 75-80 Mayor o igual a 80 0 80-85 Trazamos los puntos especificados (50, 100), (55, 84), (60, 46), (65, 22), (70, 10), (75, 2) y (80, 0) y conectamos para formar una ojiva más que como se muestra a continuación:
Pregunta 7. Durante el chequeo médico de 35 alumnos de una clase, sus pesos fueron registrados de la siguiente manera:
|
Peso (en kg) |
Numero de estudiantes |
|
menos de 38 |
0 |
|
menos de 40 |
3 |
|
menos de 42 |
5 |
|
menos de 44 |
9 |
|
menos de 46 |
14 |
|
menos de 48 |
28 |
|
Menos de 50 |
32 |
|
menos de 52 |
35 |
Dibuja una ojiva menor que tipo para los datos dados. Por lo tanto, obtenga el peso mediano del gráfico y verifique el resultado usando la fórmula. (CBSE 2009)
Solución:
Peso (en kg)
Numero de estudiantes
Clase cf menos de 38
0
36-38 0 menos de 40
3
38-40 3 menos de 42
5
40-42 2 menos de 44
9
42-44 4 menos de 46
14
44-46 5 menos de 48
28
46-48 14 Menos de 50
32
48-50 4 menos de 52
35
50-52 3
Marca los puntos (38, 0), (40, 3), (42, 5), (44, 9), (46, 14), (48, 28), (50, 32), (52, 35) en el gráfico y únelos a mano alzada para obtener una ojiva como se muestra.
Aquí N = 35 que es impar
∴
= 252 = 17,5
Desde 17.5 en el eje y, dibuje una línea paralela al eje x que se encuentre con la curva en P. Desde P, dibuje PM ⊥ eje x
∴ Mediana que es 46.5 (aprox.)
Ahora N = 17,5 se encuentra en la clase 46 – 48 (como 14 < 17,5 < 28)
∴ 46-48 es la clase mediana
Aquí l= 46, h = 2, f= 14, F= 14
∴ Mediana =
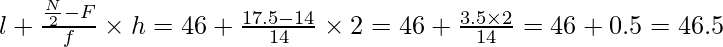
Pregunta 8. El registro anual de lluvia de una ciudad durante 66 días se da en la siguiente pestaña
|
Precipitación (en cm): |
0-10 |
10-20 |
20-30 |
30-40 |
40-50 |
50-60 |
|
Número de días: |
22 |
10 |
8 |
15 |
5 |
6 |
Calcule la precipitación mediana usando ojivas de más de tipo y menos de tipo. [Ejemplo NCERT]
Solución:
Observamos que el registro anual de precipitaciones de una ciudad menor que 0 es 0. De manera similar, menos de 10 incluye el registro anual de precipitaciones de una ciudad desde 0, así como el registro anual de precipitaciones de una ciudad desde 0-10. Asi que,
el registro de precipitación anual total de una ciudad para menos de 10 cm es 0 + 22 = 22 días. Continuando así, obtendremos menos de 20, 30, 40, 50 y 60 restantes. Además, observamos que la precipitación anual
registro de una ciudad durante 66 días es mayor o igual a 0 cm. Dado que, 22 días se encuentra en el intervalo 0-10. Por lo tanto, el registro anual de precipitaciones durante 66 – 22 = 44 días es mayor o igual a 10 cm. Continuando en este
De esta manera obtendremos restante mayor o igual a 20, 30, 40, 50 y 60.
Ahora, construimos una tabla para menos que y más que tipo.
(i) Menos que tipo
(ii) Más que tipo
Precipitación (en cm)
Número de días
Precipitación (en cm)
Número de días
menos de 0
0
Mayor o igual a 0
66
Menos de 10
0+22=22
Mayor o igual a 10
66-22=44
Menos de 20
22+10=32
Mayor o igual a 20
44-10=34
menos de 30
32+8=40
Mayor o igual a 30
34-8=26
menos de 40
40+15=55
Mayor o igual a 40
26-15=11
Menos de 50
55+5=60
Mayor o igual a 50
11-5=6
menos de 60
60+6=66
Mayor o igual a 60
6-6=0
Para dibujar menos de tipo ojiva trazamos los puntos (0,0), (10,22), (20,32), (30, 40), (40, 55), (50, 60), (60, 66) ) en el papel y unirlos a mano alzada.
Para dibujar la ojiva de más de tipo trazamos los puntos (0, 66), (10, 44), (20, 34), (30, 26), (40, 11), (50, 6) y (60, 0) en el papel cuadriculado y únelos a mano alzada.
∵ Número total de días (n) = 66
Ahora,
= 33
En primer lugar, trazamos una línea paralela al eje X en el punto de intersección de ambas ojivas, que además se intersecan en (0, 33) en el eje Y. Ahora, dibujamos una línea perpendicular al eje X en el punto de intersección de ambas ojivas,
que además se cruzan en (21.25, 0) en el eje X. Cuál es la mediana requerida usando ojivas.
Por lo tanto, la precipitación media = 21,25 cm.
Pregunta 9. La siguiente tabla da la altura de los árboles:
|
Altura |
Número de árboles |
|
menos de 7 |
26 |
|
menos de 14 |
57 |
|
menos de 21 |
92 |
|
menos de 28 |
134 |
|
menos de 35 |
216 |
|
menos de 42 |
287 |
|
menos de 49 |
341 |
|
menos de 56 |
360 |
Dibuje la ojiva ‘menor que’ y la ojiva ‘más que’.
Solución:
(i) Primero preparamos una tabla de frecuencia inferior a la siguiente:
Altura
Intervalo de clases
Frecuencia
cf
menos de 7
0-7
26
26
menos de 14
7-14
31
57
menos de 21
14-21
35
92
menos de 28
21-28
42
134
menos de 35
28-35
82
216
menos de 42
35-42
71
287
menos de 49
42-49
54
341
menos de 56
49-56
19
360
Ahora trazamos los puntos (7, 26), (14, 57), (21, 92), (28, 134), (35, 216), (42, 287), (49, 341), (56, 360) en el gráfico y luego unirse en una curva de frecuencia que es ‘menos que ojiva’
(ii) Más que ojiva:
Primero preparamos la tabla de frecuencia ‘más que’ como se muestra a continuación:
Más que
Intervalo de clases
cf
Frecuencia
más de 0
0-7
360
19
más de 7
7-14
341
54
más de 14
14-21
287
71
más de 21
21-28
216
82
más de 28
28-35
134
42
más de 35
35-42
92
35
más de 42
42-49
57
31
más de 49
49-56
26
26
más de 56
56-
0
0
Ahora trazamos los puntos (0, 360), (7, 341), (14, 287), (21, 216), (28, 134), (35, 92), (42, 57), (49, 26), (56, 0) en el gráfico y únelos en una curva a mano alzada para obtener más de una ojiva.
Pregunta 10. Las utilidades anuales obtenidas por 30 tiendas de un complejo comercial en una localidad dan lugar a la siguiente distribución:
|
Beneficio (en lakhs ₹) |
intervalos de clase |
Número de tiendas (cf) |
Frecuencia |
|
Mayor o igual a 5 |
5-10 |
30 |
2 |
|
Mayor o igual a 10 |
10-15 |
28 |
12 |
|
Mayor o igual a 15 |
15-20 |
dieciséis |
2 |
|
Mayor o igual a 20 |
20-25 |
14 |
4 |
|
Mayor o igual a 25 |
25-30 |
10 |
3 |
|
Mayor o igual a 30 |
30-35 |
7 |
4 |
|
Mayor o igual a 35 |
35-40 |
3 |
0 |
Dibuje ambas ojivas para los datos anteriores y, por lo tanto, obtenga la mediana.
Solución:
Intervalo de clases
Frecuencia
cf
5-10
3
3
10-15
4
7
15-20
3
10
20-25
4
14
25-30
2
dieciséis
30-35
12
28
35-40
2
30
Ahora traza los puntos (5, 30), (10, 28), (15, 16), (20, 14), (25, 10), (30, 7) y (35, 3) en el gráfico y únelos para obtener una curva más que.
Menos que la curva:
Ahora traza los puntos (10, 3), (15, 7), (20, 10), (25, 14), (30, 16), (35, 28) y (40, 30) en el gráfico y únelos ellos para obtener una ojiva menos ellos. Las dos curvas se intersecan en P. Desde P, dibuje PM 1 eje x, M es el
mediana que es 22.5
∴ Mediana = Rs. 22,5 mil rupias
Publicación traducida automáticamente
Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA









