Pregunta 1. La hipotenusa de un triángulo rectángulo mide 25 cm. La diferencia entre las longitudes de los otros dos lados del triángulo es de 5 cm. Encuentra las longitudes de estos lados.
Solución:
Sean x e y las longitudes de los otros dos lados del triángulo.
Por lo tanto, de acuerdo con la pregunta,
x – y = 5
o,
x = y + 5
Ahora los dos lados son de longitud y e y + 5.
Aplicando el teorema de Pitágoras en el triángulo rectángulo, obtenemos,
25 2 = y 2 + (y + 5) 2
625 = y2 + y2 + 25 + 10y
2 años 2 + 25 + 10 años = 625
2 años 2 + 10 años = 625 – 25
2 años 2 + 10 años – 600 = 0
y 2 + 5y – 300 = 0
y 2 + 20y – 15y – 300 = 0 [Por división del término medio]
y(y+20) – 15(y+20) = 0
(y – 15)(y + 20) = 0
y -15 = 0 o y + 20 = 0
y = 15 o y = -20
Como la longitud de un lado es positiva, tomaremos y = 15.
Por lo tanto,
x = y + 5
X = 15 + 5
X = 20
Los dos lados del triángulo miden 15 cm y 20 cm .
Pregunta 2. La diagonal de un campo rectangular mide 60 metros más que el lado más corto. Si el lado más largo mide 30 metros más que el lado más corto, halla los lados del campo.
Solución:
Sea x el lado más corto del rectángulo.
Ahora, de acuerdo con la pregunta, la longitud del rectángulo es x + 60 y la longitud del lado más largo del rectángulo es x + 30.
Ahora, aplicaremos el teorema de Pitágoras al triángulo rectángulo formado por la diagonal y los dos lados,
(x + 60) 2 = (x + 30) 2 + x 2
x2 + 3600 + 120x = x2 + 900 + 60x + x2
3600 – 900 = x2 + 60x – 120x
2700 = x2 – 60x
x 2 – 60x – 2700 = 0
x 2 – 90x + 30x – 2700 = 0
x(x-90) + 30(x-90) = 0
(x + 30)(x – 90) = 0
x + 30 = 0 o x – 90 = 0
x = -30 o x = 90
Tomaremos el lado positivo, es decir, x = 90
Ahora,
la longitud del lado más corto es de 90 m
la longitud de la diagonal es 90 + 60 = 150 m
la longitud del lado mayor es 90 + 30 = 120 m
Pregunta 3. La hipotenusa de un triángulo rectángulo mide 3√10 cm. Si el cateto más pequeño se triplica y el cateto más largo se duplica, la nueva hipotenusa será de 9√5 cm. ¿Cuánto miden los catetos del triángulo?
Solución:
Sea x e y el lado más pequeño y más largo del triángulo.
Ahora, aplicando el teorema de Pitágoras, obtenemos,
(3√10) 2 = x 2 + y 2
x 2 + y 2 = 90 ……… (yo)
Ahora los lados más pequeños y más largos se triplican y se duplican respectivamente,
Por tanto, los nuevos lados del triángulo serán 3x y 2y.
Aplicando el teorema de Pitágoras,
(9√5) 2 = (3x) 2 + (2y) 2
9x 2 + 4y 2 = 405 ……… (ii)
Ahora, multiplicando (i) por 4 y luego restando (i) de (ii), obtenemos
9x 2 – 5x 2 + 4y 2 – 4y 2 = 405 – 360
5×2 = 45
× 2 = 9
x = 3
Sustituyendo el valor de x en (i),
9 + y 2 = 90
y2 = 81
y = 9
La longitud del lado más pequeño es de 3 cm.
La longitud del lado más largo es de 9 cm.
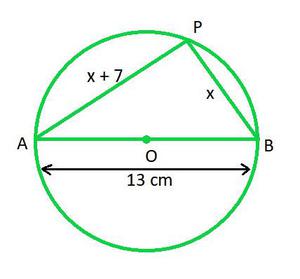
Pregunta 4. Se debe erigir un poste en un punto en el límite de un parque circular de 13 metros de diámetro de tal manera que la diferencia de sus distancias desde dos puertas fijas A y B diametralmente opuestas en el límite sea de 7 metros. ¿Es posible hacerlo? En caso afirmativo, ¿a qué distancia de las dos puertas se debe erigir el poste?
Solución:
En el círculo, sea P el polo sobre la circunferencia del círculo y los puntos A y B las dos puertas fijas diametralmente opuestas.
Sea x la longitud de PB.
Dado,
PA-PB = 7
PA = x + PB
PA = x + 7
El triángulo PQR es un triángulo rectángulo en P, ya que AB es el diámetro del círculo.
Ahora aplicando el teorema de Pitágoras,
AB2 = PA2 + PB2
13 2 = (x + 7) 2 + x 2
169 = x2 + 49 + 14x + x2
169 = 2×2 + 14x + 49
2×2 + 14x + 49 – 169 = 0
2x 2 + 14x – 120 = 0
x2 + 7x – 60 = 0
x2 + 12x – 5x – 60 = 0
x(x+12) – 5(x+12) = 0
(x – 5)(x + 12) = 0
x = 5 o x = -12
Solo x = 5 es posible.
PB = 5m
PA = 5 + 7 = 12 m
P debe montarse a una distancia de 5 m de PB y 12 m de PA.
Publicación traducida automáticamente
Artículo escrito por parasmadan15 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA