Pruebalo:
Pregunta 1. sen 5 θ = 5 sen θ – 20 sen 3 θ + 16 sen 5 θ
Solución:
Tenemos,
LHS = sen 5θ
= sen (3θ + 2θ)
= sen 3θ cos 2θ + cos 3θ sen 2θ
= (3sen θ – 4sen 3 θ) (1 – 2sen 2 θ) + (4cos 3 θ – 3cos θ) (2sen θ cos θ)
= 3 sen θ – 6 sen 3 θ – 4 sen 3 θ + 8 sen 5 θ + 8 sen θ cos 4 θ – 6 sen θ cos 2 θ
= 3sen θ – 10sen 3 θ + 8sen 5 θ + 8sen θ (1 – sen 2 θ) 2 – 6sen θ (1–sen 2 θ)
= 3 sen θ – 10 sen 3 θ + 8 sen 5 θ + 8 sen θ (1 + sen 4 θ – 2 sen 2 θ) – 6 sen θ + 6 sen 3 θ
= 3 sen θ – 4 sen 3 θ + 8 sen 5 θ + 8 sen θ + 8 sen 5 θ – 16 sen 3 θ – 6 sen θ
= 5 sen θ – 20 sen 3 θ + 16 sen 5 θ
= lado derecho
Por lo tanto, probado.
Pregunta 2. 4 (cos 3 10 o + sen 3 20 o ) = 3 (cos 10 o + sen 20 o )
Solución:
Ahora sabemos,
sen θ = cos (90–θ)
Para θ = 60 o , tenemos,
=> sen 60 o = cos 30 o
=> sen (3×20 o ) = coseno (3×10 o )
=> 3sen 20 o – 4sen 3 20 o = 4cos 3 10 o – 3cos 10 o
=> 4 cos 3 10 o + 4 sen 3 20 o = 3 cos 10 o + 3 sen 20 o
=> 4 (cos 3 10 o + sen 3 20 o ) = 3 (cos 10 o + sen 20 o )
Por lo tanto, probado.
Pregunta 3. cos 3 θ sen 3θ + sen 3 θ cos 3θ = (3 sen 4 θ)/4
Solución:
Tenemos,
LHS = cos 3 θ sen 3θ + sen 3 θ cos 3θ
= sen 3θ (cos 3θ + 3cos θ)/4 + cos 3θ (3sen θ – sen 3θ)/4
= (sen 3θ cos 3θ + 3sen 3θ cos θ + 3cos 3θ sen θ – cos 3θ sen 3θ)/4
= [3(sen 3θ cos θ + cos 3θ sen θ) ]/4
= [3sen (3θ+θ)]/4
= (3sen 4θ)/4
= lado derecho
Por lo tanto, probado.
Pregunta 4. sen 5A = 5 cos 4 A sen A – 10 cos 2 A sen 3 A + sen 5 A
Solución:
Tenemos,
IZQ = sen 5A
= pecado (3A + 2A)
= sen 3A cos 2A + cos 3A sen 2A
= (3sen A – 4sen 3 A) (2cos 2 A – 1) + (4cos 3 A – 3cos A) (2sen A cos A)
= 6 sen A cos 2 A – 3 sen A – 8 sen 3 A cos 2 A + 4 sen 3 A + 8 sen A cos 4 A – 6 sen A cos 2 A
= – 3 sen A – 8 sen 3 A cos 2 A + 4 sen 3 A + 8 sen A cos 4 A
= – 3 sen A – 10 sen 3 A cos 2 A + 2 sen 3 A cos 2 A + 4 sen 3 A + 5 sen A cos 4 A + 3 sen A cos 4 A
= 5 sen A cos 4 A – 10 sen 3 A cos 2 A – 3 sen A (1 – cos 4 A) + 2 sen 3 A (2 + cos 2 A)
= 5 sen A cos 4 A – 10 sen 3 A cos 2 A – 3 sen A (1 – cos 2 A) (1 + cos 2 A) + 2 sen 3 A (2 + cos 2 A)
= 5 sen A cos 4 A – 10 sen 3 A cos 2 A – 3 sen 3 A (1 + cos 2 A) + 2 sen 3 A (2 + cos 2 A)
= 5sen A cos 4 A – 10 sen 3 A cos 2 A – sen 3 A (3 + 3cos 2 A – 4 – 2cos 2 A)
= 5 sen A cos 4 A – 10 sen 3 A cos 2 A – sen 3 A (cos 2 A – 1)
= 5 sen A cos 4 A – 10 sen 3 A cos 2 A + sen 5 A
= lado derecho
Por lo tanto, probado.
Pregunta 5. tan A tan (A + 60 o ) + tan A tan (A – 60 o ) + tan (A + 60 o ) tan (A – 60 o ) = –3
Solución:
Tenemos,
LHS = tan A tan (A + 60 o ) + tan A tan (A – 60 o ) + tan (A + 60 o ) tan (A – 60 o )
=
=
=
=
=
= –3
= lado derecho
Por lo tanto, probado.
Pregunta 6. tan A + tan (60 o + A) – tan (60 o – A) = 3 tan 3A
Solución:
Tenemos,
LHS = tan A + tan (60 o + A) – tan (60 o – A)
=
=
=
=
=
= 3 tan 3A
= lado derecho
Por lo tanto, probado.
Pregunta 7. cuna A + cuna (60 o + A) – cuna (60 o – A) = 3 cuna 3A
Solución:
Tenemos,
LHS = cuna A + cuna (60 o + A) – cuna (60 o – A)
=
=
=
=
=
= 3 cuna 3A
= lado derecho
Por lo tanto, probado.
Pregunta 8. cuna A + cuna (60 o + A) + cuna (120 o + A) = 3 cuna 3A
Solución:
Tenemos,
LHS = cuna A + cuna (60 o + A) + cuna (120 o + A)
= cuna A + cuna (60 o + A) – cuna (180 – (120 o + A))
= cuna A + cuna (60 o + A) – cuna (60 o – A)
=
=
=
=
=
= 3 cuna 3A
= lado derecho
Por lo tanto, probado.
Pregunta 9. 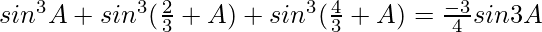
Solución:
Tenemos,
IZQ =
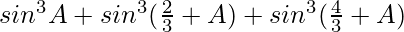
=
=
=
=
=
=
![Rendered by QuickLaTeX.com \frac{1}{4}\left[3sinA-3sin3A+6cos\frac{π}{3}sin(-A)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-374b860ebf0e082b17843ff2da776e8e_l3.png)
=
=
= lado derecho
Por lo tanto, probado.
Pregunta 10. |sen θ sin (60–θ) sin (60+θ)| ≤ 1/4 para todos los valores de θ.
Solución:
Tenemos,
= |sin θ sin (60–θ) sin (60+θ)|
= |sen θ (sen 2 60 – sen 2 θ)|
= |sen θ (3/4 – sen 2 θ)|
= |sen θ/4 (3 – 4sen 2 θ)|
= |1/4 (3sen θ – 4sen 3 θ)|
= |1/4 (sen 3θ)| ≤ 1/4
Por lo tanto, probado.
Pregunta 11. |cos θ cos (60–θ) cos (60+θ)| ≤ 1/4 para todos los valores de θ .
Solución:
Tenemos,
= |cos θ cos (60–θ) cos (60+θ)|
= |cos θ (cos 2 60 – sen 2 θ)|
= |cos θ (1/4 – sen 2 θ)|
= |cos θ/4 (1 – 4sen 2 θ)|
= |cos θ/4 (1 – 4 (1 – cos 2 θ))|
= |cos θ/4 (–3 + 4cos 2 θ)|
= |1/4 (4cos 3 θ – 3cos θ)|
= |1/4 (cos 3θ)| ≤ 1/4
Por lo tanto, probado.
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
![Procesado por QuickLaTeX.com tanA\left[\frac{(tanA+tan60^0)(1+tanAtan60^0)}{1-tan^2Atan^260^0}\right]+tanA\left[\frac{(tanA-tan60^0)(1-tanAtan60^0)}{1-tan^2Atan^260^0}\right]+\left[\frac{tan^2A-tan^260^0}{1-tan^2tan^260^0}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a19b02e537475fa69640889636f36918_l3.png)
![Rendered by QuickLaTeX.com (\frac{3sinA-sin3A}{4})+\left[\frac{3sin(\frac{2π}{3}+A)-sin3(\frac{2π}{3}+A)}{4}\right]+\left[\frac{3sin(\frac{4π}{3}+A)-sin3(\frac{4π}{3}+A)}{4}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3cbdbe7b0c6167a4174d47408262d9c9_l3.png)