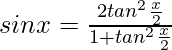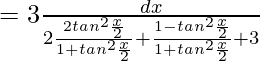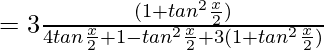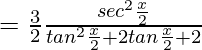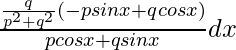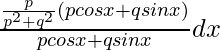Clase 12 Soluciones RD Sharma – Capítulo 19 Integrales indefinidas – Ejercicio 19.24

Pregunta 1. ∫dx/(1-cotx)

Solución:

Tenemos,

Sea I=∫dx/(1-cotx)

$=∫\frac{dx}{1-\frac{cosx}{sinx}}$

=∫senx.dx/(senx-cosx)

=(1/2)∫2senx.dx/(senx-cosx)

$=\frac{1}{2}∫\frac{sinx+cosx+sinx-cosx}{sinx-cosx}dx$

=(1/2)∫[(senx+cosx)dx/(senx-cosx)]+(1/2)∫dx

Sea, senx-cosx=z

Derivando ambos lados tenemos

(cosx+senx)dx=dz

=(1/2)Log|senx-cosx|+(x/2)+C (Aquí C es la constante de integración)

Pregunta 2. ∫dx/(1-tanx)

Solución:

Tenemos,

Sea I=∫dx/(1-tanx)

$=∫\frac{dx}{1-\frac{sinx}{cosx}}$

=∫cosx.dx/(cosx-senx)

=(1/2)∫2cosx.dx/(cosx-senx)

$=\frac{1}{2}∫\frac{cosx+sinx+cosx-sinx}{cosx-sinx}dx$

=(1/2)∫[(cosx+senx)dx/(cosx-senx)]+(1/2)∫dx

Sea, cosx-senx=z

Derivando ambos lados tenemos

-(senx+cosx)dx=dz

(senx+cosx)dx=-dz

=(x/2)-(1/2)Log|cosx-senx|+C (Aquí C es la constante de integración)

Pregunta 3. ∫[(3+2cosx+4senx)/(2senx+cosx+3)]dx

Solución:

Tenemos,

Sea I=∫[(3+2cosx+4senx)/(2senx+cosx+3)]dx

ahora sustituyendo el numerador

3+2cosx+4senx=A(d/dx)(2senx+cosx+3)+B(2senx+cosx+3)+C

3+2cosx+4senx=A(2cosx-senx)+B(2senx+cosx+3)+C

3+2cosx+4senx=2Acosx-Asenx+2Bsenx+Bcosx+3B+C

3+2cosx+4senx=(3B+C)+(2A+B)cosx+(2B-A)senx

(3B+C)=3 (yo)

(2A+B)=2 (ii)

(2B-A)=4 (iii)

Al resolver las ecuaciones anteriores,

A=0 ,B=2 ,C=-3

$I=∫\frac{2(2sinx+cosx+3)-3}{2sinx+cosx+3)}$

=2∫dx-∫3/(2senx+cosx+3)

=yo ₁ -yo ₂

1 = _2∫dx

=2x

yo ₂ =∫3/(2senx+cosx+3)

Sustituyendo $cosx=\frac{1-tan^2\frac{x}{2}}{1+tan^2\frac{x}{2}}$ y $sinx=\frac{2tan^2\frac{x}{2}}{1+tan^2\frac{x}{2}}$

$=3∫\frac{dx}{2×\frac{2tan^2\frac{x}{2}}{1+tan^2\frac{x}{2}}+\frac{1-tan^2\frac{x}{2}}{1+tan^2\frac{x}{2}}+3}$

$=3∫\frac{(1+tan^2\frac{x}{2})}{4tan\frac{x}{2}+1-tan^2\frac{x}{2}+3(1+tan^2\frac{x}{2})}$

$=\frac{3}{2}∫\frac{sec^2\frac{x}{2}}{tan^2\frac{x}{2}+2tan\frac{x}{2}+2}$

Sea tan(x/2)=z

Diferenciando ambos lados,

(1/2)seg ² (x/2)dx=dz

=3∫dz/(z ² +2z+2)

=3∫dz/(z ² +2z+1+1)

=3∫dz/{(z+1) ² +1 ² }

=3tan ^-1 (z+1)

Poniendo el valor de z

=3tan ^-1 (tanx/2+1)

I ₂ =3tan ^-1 (tanx/2+1)

yo=yo ₁ -yo ₂

=2x-3tan ^-1 (tanx/2+1)+C (Aquí C es la constante de integración)

Pregunta 4. ∫dx/(p+qtanx)

Solución:

Tenemos,

Sea I=∫dx/(p+qtanx)

=∫[cosx/(pcosx+qsenx)]dx

ahora sustituyendo el numerador

cosx=A(d/dx)(pcosx+qsenx)+B(pcosx+qsenx)+C

cosx=A(-psinx+qcosx)+B(pcosx+qsenx)+C

cosx=senx(Bq-Ap)+cosx(Bp+Aq)+C

Al comparar ambos lados,

C=0,

pb+ac=1,

Bq-Ap=0,

Resolviendo la ecuación anterior,

A=q/(p ² +q ² ) y B=p/(p ² +q ² )

$I=∫\frac{\frac{q}{p^2+q^2}(-psinx+qcosx)+\frac{p}{p^2+q^2}(pcosx+qsinx)}{pcosx+qsinx}$ [Tex]I=∫\frac{\frac{q}{p^2+q^2}(-psinx+qcosx)+\frac{p}{p^2+q^2}(pcosx+qsenx)} {pcosx+qsinx}dx[/Tex]

yo = yo ₁ + yo ₂

yo ₁ = $∫\frac{\frac{q}{p^2+q^2}(-psinx+qcosx)}{pcosx+qsinx}dx$

=q/(p ² +q ² )log|pcosx+qsenx|

yo ₂ = $∫\frac{\frac{p}{p^2+q^2}(pcosx+qsinx)}{pcosx+qsinx}dx$

=px/(p ² +q ² )

I=q/(p ² +q ² )log|pcosx+qsinx|+px/(p ² +q ² )+C (Aquí C es una constante de integración)

Pregunta 5. ∫[(5cosx+6)/(2cosx+senx+3)]dx

Solución:

Tenemos,

Sea I=∫[(5cosx+6)/(2cosx+senx+3)]dx

ahora sustituyendo el numerador

5cosx+6=A(d/dx)(2cosx+senx+3)+B(2cosx+senx+3)+C

5cosx+6=A(-2senx+cosx)+B(2cosx+senx+3)+C

5cosx+6=senx(B-2A)+cosx(2B+A)+3B+C

Al comparar ambos lados,

3B+C=6,

2B+A=5,

B-2A=0,

Resolviendo la ecuación anterior,

A=1, B=2 yc=0

$I=∫\frac{(-2sinx+cosx)+2(2cosx+sinx+3)}{2cosx+sinx+3}dx$

yo = yo ₁ + yo ₂

I ₁ =∫[(-2senx+cosx)/(2cosx+senx+3)]dx

I ₁ =log|2cosx+senx+3|

yo ₂ =2∫dx

yo ₂ = 2x

I=log|2cosx+senx+3|+2x+C (Aquí C es la constante de integración)

Pregunta 6. ∫[(2senx+3cosx)/(3senx+4cosx)]dx

Solución:

Tenemos,

Sea I=∫[(2senx+3cosx)/(3senx+4cosx)]dx

ahora sustituyendo el numerador

2senx+3cosx=A(d/dx)(3senx+4cosx)+B(3senx+4cosx)+C

2senx+3cosx=A(3cosx-4senx)+B(3senx+4cosx)+C

2senx+3cosx=senx(3B-4A)+cosx(4B+3A)+3B+C

Al comparar ambos lados,

3B-4A=2,

4B+3A=3,

Resolviendo la ecuación anterior,

A=1/25, B=18/25 y C=0

$I=∫\frac{\frac{1}{25}(3cosx-4sinx)+\frac{18}{25}(3sinx+4cosx)}{(3sinx+4cosx)}dx$

yo = yo ₁ + yo ₂

I ₁ =(1/25)∫[(3cosx-4senx)/(3senx+4cosx)]dx

I ₁ =(1/25)log|3senx+4cosx|

Yo ₂ =(18/25)∫dx

yo ₂ =(18x/25)

I=(1/25)log|3sinx+4cosx|+(18x/25)+C (Aquí C es la constante de integración)

Pregunta 7. ∫dx/(3+4cotx)

Solución:

Tenemos,

Sea I=∫dx/(3+4cotx)

=∫[(senx)/(3senx+4cosx)]dx

ahora sustituyendo el numerador

senx=A(d/dx)(3senx+4cosx)+B(3senx+4cosx)+C

senx=A(3cosx-4senx)+B(3senx+4cosx)+C

senx=senx(3B-4A)+cosx(4B+3A)+3B+C

Al comparar ambos lados,

3B-4A=1,

4B+3A=0,

Resolviendo la ecuación anterior,

A=-4/25, B=3/25 y C=0

$I=∫\frac{\frac{-4}{25}(3cosx-4sinx)+\frac{3}{25}(3sinx+4cosx)}{(3sinx+4cosx)}dx$

yo = yo ₁ + yo ₂

Yo ₁ =(-4/25)∫[(3cosx-4senx)/(3senx+4cosx)]dx

I ₁ =(-4/25)log|3senx+4cosx|

Yo ₂ =(3/25)∫dx

Yo ₂ = (3x/25)

I=(3x/25)-(4/25)log|3senx+4cosx|+(18x/25)+C (Aquí C es la constante de integración)

Pregunta 8. ∫[(2tanx+3)/(3tanx+4)]dx

Solución:

Tenemos,

Sea I=∫[(2tanx+3)/(3tanx+4)]dx

=∫[(2senx+3cosx)/(3senx+4cosx)]dx

ahora sustituyendo el numerador

2senx+3cosx=A(d/dx)(3senx+4cosx)+B(3senx+4cosx)+C

2senx+3cosx=A(3cosx-4senx)+B(3senx+4cosx)+C

2senx+3cosx=senx(3B-4A)+cosx(4B+3A)+C

Al comparar ambos lados,

3B-4A=2,

4B+3A=3,

Resolviendo la ecuación anterior,

A=1/25, B=18/25 y C=0

$I=∫\frac{\frac{1}{25}(3cosx-4sinx)+\frac{18}{25}(3sinx+4cosx)}{(3sinx+4cosx)}dx$

yo = yo ₁ + yo ₂

I ₁ =(1/25)∫[(3cosx-4senx)/(3senx+4cosx)]dx

I ₁ =(1/25)log|3senx+4cosx|

Yo ₂ =(18/25)∫dx

yo ₂ =(18x/25)

I=(1/25)log|3sinx+4cosx|+(18x/25)+C (Aquí C es la constante de integración)

Pregunta 9. ∫dx/(4+3tanx)

Solución:

Tenemos,

Sea I=∫dx/(4+3tanx)

=∫[(cosx)/(4cosx+3senx)]dx

ahora sustituyendo el numerador

cosx=A(d/dx)(3senx+4cosx)+B(3senx+4cosx)+C

cosx=A(3cosx-4senx)+B(3senx+4cosx)+C

cosx=senx(3B-4A)+cosx(4B+3A)+C

Al comparar ambos lados,

3B-4A=0,

4B+3A=3,

Resolviendo la ecuación anterior,

A=3/25, B=4/25 y C=0

$I=∫\frac{\frac{3}{25}(3cosx-4sinx)+\frac{4}{25}(3sinx+4cosx)}{(3sinx+4cosx)}dx$

yo = yo ₁ + yo ₂

I ₁ =(3/25)∫[(3cosx-4senx)/(3senx+4cosx)]dx

I ₁ =(3/25)log|3senx+4cosx|

Yo ₂ =(4/25)∫dx

Yo ₂ = (4x/25)

I=(3/25)log|3senx+4cosx|+(4x/25)+C (Aquí C es la constante de integración)

Pregunta 10. ∫[(8cotx+1)/(3cotx+2)]dx

Solución:

Tenemos,

Sea I=∫[(8cotx+1)/(3cotx+2)]dx

=∫[(8cosx+senx)/(3cosx+2senx)]dx

ahora sustituyendo el numerador

8cosx+senx=A(d/dx)(3cosx+2senx)+B(3cosx+2senx)+C

8cosx+senx=A(-3senx+2cosx)+B(3cosx+2senx)+C

8cosx+senx=senx(2B-3A)+cosx(3B+2A)+C

Al comparar ambos lados,

2B-3A=1,

3B+2A=3,

Resolviendo la ecuación anterior,

A=1, B=2 y C=0

$I=∫\frac{(-3sinx+2cosx)+2(3cosx+2sinx)}{(3cosx+2sinx)}dx$

yo = yo ₁ + yo ₂

I ₁ =∫[(-3senx+2cosx)/(3cosx+2senx)]dx

I ₁ =log|3cosx+2senx|

yo ₂ =2∫dx

yo ₂ = 2x

I=log|3cosx+2sinx|+2x+C (Aquí C es la constante de integración)

Pregunta 11. ∫[(4senx+5cosx)/(5senx+4cosx)]dx

Solución:

Tenemos,

Sea I=∫[(4senx+5cosx)/(5senx+4cosx)]dx

ahora sustituyendo el numerador

4senx+5cosx=A(d/dx)(5senx+4cosx)+B(5senx+4cosx)+C

4senx+5cosx=A(5cosx-4senx)+B(5senx+4cosx)+C

4senx+5cosx=senx(5B-4A)+cosx(4B+5A)+C

Al comparar ambos lados,

5B-4A=4,

4B+5A=5,

Resolviendo la ecuación anterior,

A=9/41, B=40/41 y C=0

$I=∫\frac{\frac{9}{41}(5cosx-4sinx)+\frac{40}{41}(5sinx+4cosx)}{(5sinx+4cosx)}dx$

yo = yo ₁ + yo ₂

I ₁ =(9/41)∫[(5cosx-4senx)/(5senx+4cosx)]dx

I1=(9/41)log|5senx+4cosx|

Yo ₂ =(40/41)∫dx

Yo ₂ = (40x/41)

I=(9/41)log|5sinx+4cosx|+(40x/41)+C (Aquí C es la constante de integración)

Publicación traducida automáticamente

Artículo escrito por vivekray59 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. ∫dx/(1-cotx)

Pregunta 2. ∫dx/(1-tanx)

Pregunta 3. ∫[(3+2cosx+4senx)/(2senx+cosx+3)]dx

Pregunta 4. ∫dx/(p+qtanx)

Pregunta 5. ∫[(5cosx+6)/(2cosx+senx+3)]dx

Pregunta 6. ∫[(2senx+3cosx)/(3senx+4cosx)]dx

Pregunta 7. ∫dx/(3+4cotx)

Pregunta 8. ∫[(2tanx+3)/(3tanx+4)]dx

Pregunta 9. ∫dx/(4+3tanx)

Pregunta 10. ∫[(8cotx+1)/(3cotx+2)]dx

Pregunta 11. ∫[(4senx+5cosx)/(5senx+4cosx)]dx

Deja una respuesta Cancelar la respuesta