Pregunta 1. Encuentra el área en el primer cuadrante delimitado por la parábola y = 4x 2 y las líneas x = 0, y = 1 y y = 4.
Solución:
De la pregunta se da que,
Líneas, x = 0, y = 1, y = 4
Parábola y = 4x 2 … [ecuación (i)]
Entonces, la ecuación (i) representa una parábola con vértice (0, 0) y eje como eje y. x = 0 es el eje y e y = 1, y = 4 son líneas paralelas al eje x que pasan a través de (0, 1) y (0, 4) respectivamente, como se muestra en el bosquejo aproximado a continuación,
Ahora, tenemos que encontrar el área de ABCDA,
Entonces, el área se puede encontrar tomando una pequeña porción en cada región de ancho Δy,
Y longitud = x
El área de la parte cortada será como si fuera un rectángulo = x Δy
Entonces, este rectángulo puede moverse horizontalmente desde y = 1 hasta x = 4
El área requerida de la región delimitada entre las líneas = Región ABCDA
Dado, y = 4x 2
x =
En la integración, obtenemos,
Ahora, aplicando límites obtenemos,
Por lo tanto, el área requerida es
unidades cuadradas.
Pregunta 2. Encuentra el área de la región delimitada por x 2 = 16y, y = 1, y = 4 y el eje y en el cuadrante.
Solución:
De la pregunta se da que,
Región en el primer cuadrante delimitada por y = 1, y = 4
Parábola x 2 = 16y … [ecuación (i)]
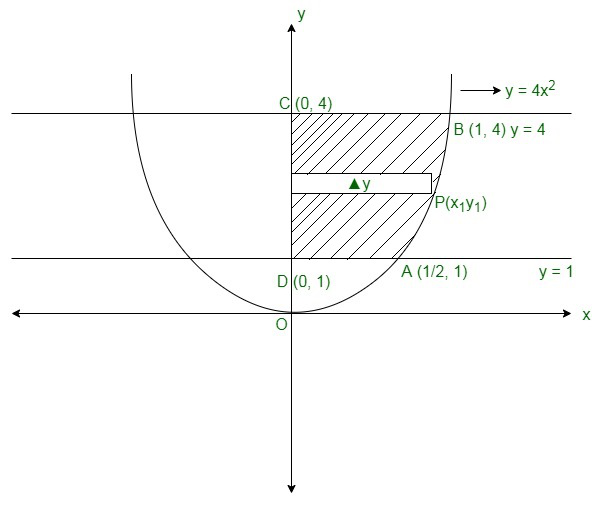
Entonces, la ecuación (i) representa una parábola con vértice (0, 0) y eje como el eje y, como se muestra en el bosquejo aproximado a continuación,
Ahora, tenemos que encontrar el área de ABCDA,
Entonces, el área se puede encontrar tomando una pequeña porción en cada región de ancho Δy,
Y longitud = x
El área de la parte cortada será como si fuera un rectángulo = x Δy
Entonces, este rectángulo puede moverse horizontalmente desde y = 1 hasta x = 4
El área requerida de la región delimitada entre las líneas = Región ABCDA
Dado, x 2 = 16y
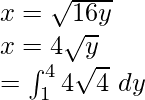
Al integrar obtenemos,
Dado, x 2 = 16y
Al integrar obtenemos,
Ahora, aplicando límites obtenemos,
Por lo tanto, el área requerida es
unidades cuadradas.
Pregunta 3. Halla el área de la región delimitada por x 2 = 4ay y su latus rectum .
Solución:
Tenemos que encontrar el área de la región acotada por x 2 = 4ay
Después,
Área de la región =
Al integrar obtenemos,
=
Ahora aplicando límites,
Por lo tanto, el área de la región es
unidades cuadradas.
Pregunta 4. Encuentra el área de la región delimitada por x 2 + 16y = 0 y su lado recto.
Solución:
Tenemos que encontrar el área de la región acotada por x 2 + 16y = 0
Después,
Área de la región =
Al integrar obtenemos,
=
Ahora aplicando límites,
Por lo tanto, el área de la región es
unidades cuadradas.
Pregunta 5. Encuentra el área de la región delimitada por la curva ay 2 = x 3 , el eje y y las líneas y = a y y = 2a.
Solución:
Tenemos que encontrar el área de la región limitada por la curva ay 2 = x 3 , y las rectas y = aey = 2a.
Después,
Área de la región =
Al integrar obtenemos, =
Ahora aplicando límites obtenemos, =
Publicación traducida automáticamente
Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
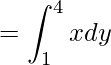
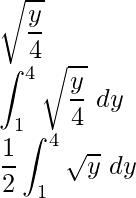
![Rendered by QuickLaTeX.com \displaystyle=\frac{1}{2}\left[\frac{2}{3}y\sqrt y\right]_1^4](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7a5afc58e19f78b018a689d2132e4b17_l3.png)
![Rendered by QuickLaTeX.com = \frac{1}{2} \left[\left(\frac{2}{3} × 4 × \sqrt4\right) - \left(\frac{2}{3} × 1 × \sqrt1\right)\right]\\ = \frac{1}{2} \left[\frac{16}{3} - \frac{2}{3}\right]\\ = \frac{1}{2} \left[\frac{(16 - 2)}{3}\right]\\ = \frac{1}{2} \left[\frac{14}{3}\right]\\ = \frac{7}{3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-98a7159906bf2788bf40acf35d407d25_l3.png)

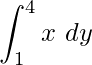
![Rendered by QuickLaTeX.com =4\left[\frac{2}{3}y\sqrt y\right]^4_1\\ =\int_1^4x\ dy](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3b6b87e68589ec7e06420c007febf5e7_l3.png)
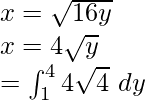
![Rendered by QuickLaTeX.com = 4 \left[\left(\frac{2}{3} × 4 × \sqrt4\right) - \left(\frac{2}{3}× 1 × \sqrt1\right)\right]\\ = 4 \left[\frac{16}{3} - \frac{2}{3}\right]\\ = 4 \left[\frac{(16 - 2)}{3}\right]\\ = 4 \left[\frac{14}{3}\right]\\ = \frac{56}{3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3738bb7a37d008697bbe4e3c7d74bede_l3.png)

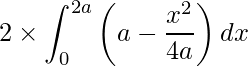
![Rendered by QuickLaTeX.com 2\times\left[ax-\frac{x^3}{12a}\right]_0^{2a}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2800dc6fde0898bf4e28911ab3b6cf04_l3.png)
![Rendered by QuickLaTeX.com = 2 × \left[(a (2a - 0)) - \frac{((2a)^3 - 0^3)}{12a}\right]\\ = 2 × \left[(2a^2) - \frac{8a^3}{12a}\right]\\ = 2 × \left[\frac{(24a^3 - 8a^3)}{12a}\right]\\ = 2 × \left[\frac{16a^3}{12a}\right]\\ = 2 × \left[\frac{4a^2}{3}\right]\\ = \frac{8a^2}{3}\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-501b64a856ac050d3c4b420bcb3f6878_l3.png)

![Rendered by QuickLaTeX.com \displaystyle2\times\int_0^{8}\left[-\frac{x^2}{16}-(-4)\right]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-926b33bbe17722397fbc082ad47ec1e5_l3.png)
![Rendered by QuickLaTeX.com 2\times\left[4x-\frac{x^3}{48}\right]_0^{8}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-26d059a045da0dcb616a845c3befc9b9_l3.png)
![Rendered by QuickLaTeX.com = 2 × \left[(4 (8 - 0)) - \frac{((8)^3 - 0^3)}{48}\right]\\ = 2 × \left[(32) - \frac{512}{48}\right]\\ = 2 × \left[(32)-\frac{32}{3}\right]\\ = 2 × \left[\frac{96-32}{3}\right]\\ = 2 × \left[\frac{64}{3}\right]\\ = \frac{128}{3}\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-91d107eabe397fc95b86254c06b0cad6_l3.png)

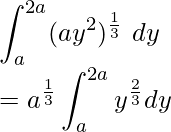
![Rendered by QuickLaTeX.com a^{\frac{1}{3}}\left[\frac{3}{5}y^{\frac{5}{3}}\right]_0^{2a}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8aad58308b56da81234acb5891bcd1ba_l3.png)