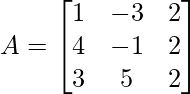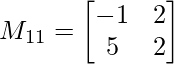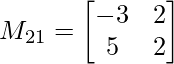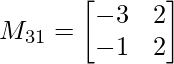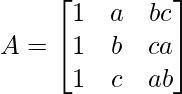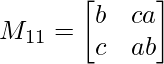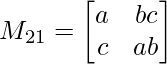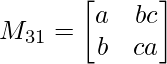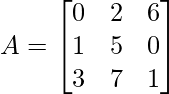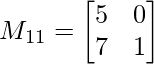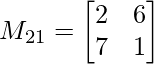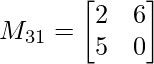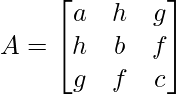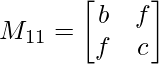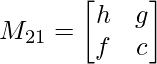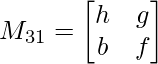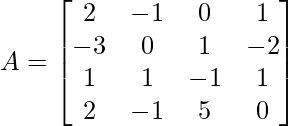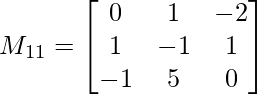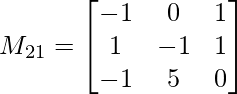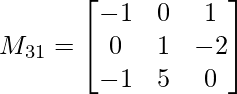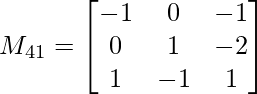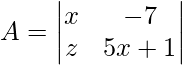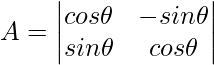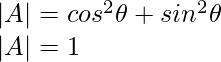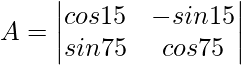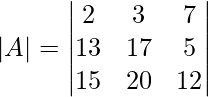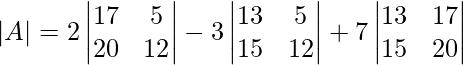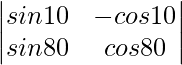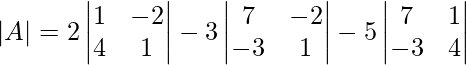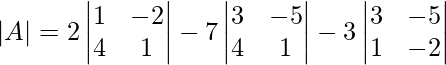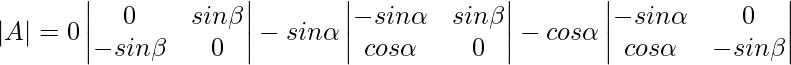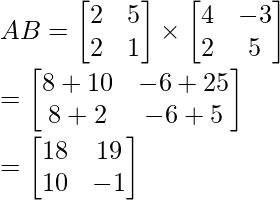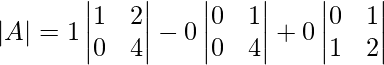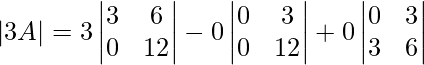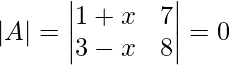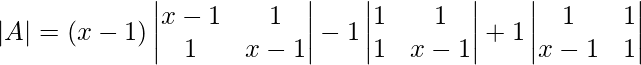Pregunta 1: escriba los menores y cofactores de cada elemento de la primera columna de las siguientes arrays y, por lo tanto, evalúe el determinante.
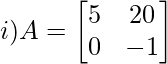
Solución:
i) Sean M ij y C ij el menor y cofactor del elemento. Se colocan en la i -ésima fila y la j -ésima columna.
Aquí, un 11 = 5
Menor de a 11 = M 11 = -1
Nota: En una array de 2 × 2, se obtiene menor para un elemento en particular, al eliminar esa fila y columna donde el elemento está presente.
Menor de a 12 = M 12 = 0
Menor de un 21 = M 21 = 20
Menor de a 22 = M 22 = 0
Como M 12 y M 22 son cero, no los consideramos. Por lo tanto, tenemos solo dos menores para este determinante.
METRO 11 = -1 y METRO 21 = 20
Ahora, los cofactores para los determinantes son
C 11 = (-1) 1+1 x M 11 {∵Cij =(-1)1+1 x Mij}
= (+1)x(-1)
= -1
C 21 = (-1) 2+1 x M 21
= (-1 ) 3×20
= -20
Evaluando el determinante,
|A| = un 11 x C 11 + un 21 x C 21
=5x(-1) + 0x(-20)
= -5
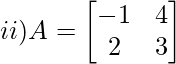
Solución:
Deje que M ij y C ij representen a un elemento menor y cofactor. Se colocan en la i -ésima fila y la j -ésima columna.
Menor de un 11 = M 11 = 3
Nota: En una array de 2 × 2, se obtiene menor para un elemento en particular, al eliminar esa fila y columna donde el elemento está presente.
Menor de un 21 = M 21 = 4
Ahora, los cofactores para los determinantes son
C 11 = (-1) 1+1 x METRO 11 {∵Cij =(-1)i+jx Mij}
= (+1) x 3
= 3
C 21 = (-1) 2+1 x M 21
= (-1 ) 3×4
= -4
Evaluando el determinante,
|A| = un 11 x C 11 + un 21 x C 21
=-1×3 + 2x(-4)
=-11
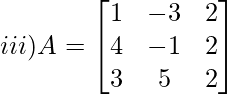
Solución:
Deje que M ij y C ij representen a un elemento menor y cofactor. Se colocan en la i -ésima fila y la j -ésima columna.
C ij = (-1) i+j x M ij
Dado,
Tenemos,
METRO 11 = -1×2 – 5×2
M 11 = -12
METRO 21 = -3×2 – 5×2
METRO 21 = -16
METRO 31 = -3×2 – (-1) x 2
M 31 = -4
Los cofactores del determinante son los siguientes,
C 11 = (-1) 1+1 x M 11
= 1x-12
= -12
C 21 = (-1) 2+1 x M 21
= (-1) 3 x -16
= 16
C 31 = (-1) 3+1 x M 31
= (1) 4 × (-4)
= -4
Para evaluar el determinante, expanda a lo largo de la primera columna,
|A| = un 11 x C 11 + un 21 x C 21 + un 31 x C 31
=1x(-12) + 4×16 + 3x(-4)
= -12 + 64 – 12
= 40
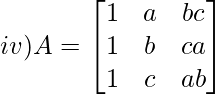
Solución:
Deje que M ij y C ij representen a un elemento menor y cofactor. Se colocan en la i-ésima fila y la j-ésima columna.
Además, C ij = (-1) i+j x M ij
Dado,
Tenemos,
M 11 = bx ab – cx ca
M 11 = ab 2 – ac 2
M 21 = hacha ab – cx bc
METRO 21 = un 2 segundo – c 2 segundo
M 31 = hacha ca – bx bc
METRO 31 = un 2 do – segundo 2 do
Los cofactores del determinante son los siguientes,
C 11 = (-1) 1+1 x M 11
= 1 x (ab 2 – ac 2 )
= ab 2 – ac 2
C 21 = (-1) 2+1 x M 21
= (-1) 3 x (a 2 b – c 2 b)
= do 2 segundo – un 2 segundo
C 31 = (-1) 3+1 x M 31
= (1) 4 x (a 2 c – b 2 c)
= un 2 do – segundo 2 do
Para evaluar el determinante, expanda a lo largo de la primera columna,
|A| = un 11 x C 11 + un 21 x C 21 + un 31 x C 31
=1 x (ab 2 – ac 2 ) + 1 x (c 2 b – a 2 b) + 1 x (a 2 c – b 2 c)
= ab 2 – ac 2 + c 2 b – a 2 b + a 2 c – b 2 c
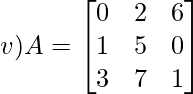
Solución:
Deje que M ij y C ij representen a un elemento menor y cofactor. Se colocan en la i -ésima fila y la j -ésima columna.
C ij = (-1) i+j x M ij
Dado,
Tenemos,
METRO 11 = 5×1 – 7×0
METRO 11 = 5
METRO 21 = 2×1 – 7×6
METRO 21 = -40
METRO31 = 2×0 – 5× 6
M 31 = -30
Los cofactores del determinante son los siguientes,
C 11 = (-1) 1+1 x M 11
= 1×5
= 5
C 21 = (-1) 2+1 x M 21
= (-1) 3 × -40
= 40
C 31 = (-1) 3+1 x M 31
= (1) 4 × (-30)
= -30
Para evaluar el determinante, expanda a lo largo de la primera columna,
|A| = un 11 x C 11 + un 21 x C 21 + un 31 x C 31
=0x5 + 1×40 + 3x(-20)
= 0 + 40 – 90
= 50
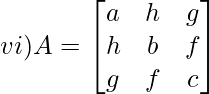
Solución:
Deje que M ij y C ij representen a un elemento menor y cofactor. Se colocan en la i -ésima fila y la j -ésima columna.
C ij = (-1) i+j x M ij
Dado,
Tenemos,
M 11 = bxc – fxf
METRO 11 = bc – f 2
M 21 = hxc – fxg
M 21 = hc – fg
M 31 = hxf – bxg
M 31 = hf – fondo
Los cofactores del determinante son los siguientes,
C 11 = (-1) 1+1 x M 11
= 1x (bc – f 2 )
= bc – f 2
C 21 = (-1) 2+1 x M 21
= (-1) 3 x (hc – fg)
= fg – hc
C 31 = (-1) 3+1 x M 31
= (1) 4 x (hf – bg)
= hf – bg
Para evaluar el determinante, expanda a lo largo de la primera columna,
|A| = un 11 x C 11 + un 21 x C 21 + un 31 x C 31
=ax (bc – f 2 ) + hx (fg – hc) + gx (hf – bg)
= abc – af 2 + hgf – h 2 c + ghf –bg 2
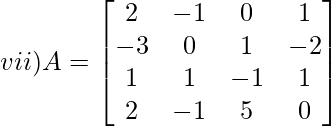
Solución:
Deje que M ij y C ij representen a un elemento menor y cofactor. Se colocan en la i -ésima fila y la j -ésima columna
Además, C ij = (-1) i+j x M ij
Dado,
De la array que tenemos,
M 11 = 0(-1 x 0 – 5 x 1) – 1(1 x 0 – (-1) x 1) + (-2)(1 x 5 – (-1) x (-1))
M 11 = -9
M 21 = -1(-1 x 0 – 5 x 1) – 0(1 x 0 – (-1) x 1) + (1 x 5 – (-1) x (-1))
METRO 21 = 9
M 31 = -1(1 x 0 – 5 x (-2)) – 0(0 x 0 – (-1) x (-2)) + 1(0 x 5 – (-1) x 1)
M 31 = -9
M 41 = -1(1 x 1 – (-1) x (-2)) – 0(0 x 1 – 1 x (-2)) + 1(0 x (-1) – 1 x 1)
METRO 41 = 0
Los cofactores del determinante son los siguientes,
C 11 = (-1) 1+1 x M 11
= 1x (-9)
= -9
C 21 = (-1) 2+1 x M 21
= (-1 ) 3×9
= -9
C 31 = (-1) 3+1 x M 31
= (-1) 4 x -9
= -9
C 41 = (-1) 4+1 x M 41
= (-1 ) 5×0
= 0
Para evaluar el determinante, expanda a lo largo de la primera columna,
|A| = un 11 x C 11 + un 21 x C 21 + un 31 x C 31 + un 41 x C 41
=2 x (-9) + (-3) x (-9) + 1 x (-9) + 2 x 0
= -18 + 27 – 9
= 0
Pregunta 2: Evalúa los siguientes determinantes
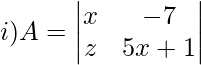
Solución:
Dado,
Multiplicando en cruz los valores dentro del determinante,
|A| = (5x + 1) – (-7)x
|A| = 5x 2 = 8x
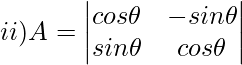
Solución:
Dado,
{
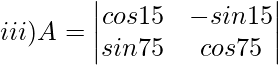
Solución:
Dado,
Sustituya esto en |A| así obtenemos,
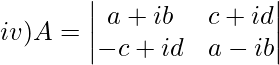
Solución:
∣A∣ = (a+ib)(a−ib)−(c+id)(−c+id)
Expandiendo los paréntesis obtenemos,
∣A∣=(a+ib)(a−ib)+(c+id)(c−id)
|A| = un 2 -i 2 segundo 2 + c 2 -i 2 re 2
Sabemos que i 2 = -1
|A| = a 2 -1b 2 +c 2 -(-1)d 2
|A| = a 2 + b 2 + c 2 + d 2
Pregunta 3: Evalúa lo siguiente:
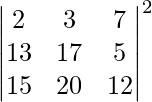
Solución:
Multiplicación cruzada de los términos en |A|
Pregunta 4: Demuestre que,
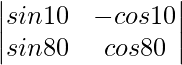
Solución:
Método 1:
Dado,
Método 2:
Pregunta 5: Evalúe el siguiente determinante por dos métodos.
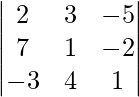
Solución:
Método 1
Método 2
Aquí está el Método Sarus, adjuntamos las dos primeras columnas.
Expandiéndose a lo largo de la segunda columna,
∣A∣ = 2(1×1−4×(−2))−7(3×1−4×(−5))−3(3×(−2)−1×(−5))
∣A ∣ = 2(1+8)−7(3+20)−3(−6+5)
∣A∣ = 2×9−7×23−3×(−1)
∣A∣ = 18−161+3
∣A∣ = −140
Pregunta 6: Evalúa lo siguiente:
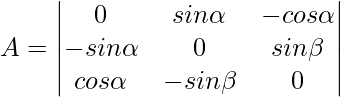
Solución:
∣A∣ = 0(0−sinβ(−sinβ))−sinα(−sinα×0−sinβcosα)−cosα((−sinα)(−sinβ)−0×cosα)
∣A∣ = 0+sinαsinβcosα−cosαsinαsinβ
∣ A∣ = 0
Pregunta 7:
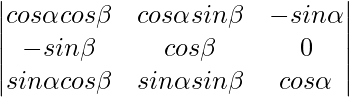
Solución:
Desarrolla C3, tenemos
∣A∣ = sinα(−sinαsen 2 β − cos 2 βsinα) + cosα(cosαcos 2 β + cosαsin 2 β)
∣A∣ = sin2α(sen 2 β + cos 2 β) + cos 2 α( cos 2 β + sen 2 β)
∣A∣ = sen 2 α(1) + cos 2 α(1)
∣A∣ = 1
Pregunta 8: Si 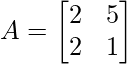
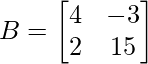 verifica que ∣AB∣ = ∣A∣∣B∣
verifica que ∣AB∣ = ∣A∣∣B∣
Solución:
Tomemos LHS,
∣AB∣ = −18−190
∣AB∣ = −208Ahora tomando RHS y calculando,
∣A∣ = 2−10
∣A∣ = −8
∣B∣ = 20−(−6)
∣B∣ = 26
∣A∣∣B∣ = −8×26
∣A∣∣B∣ = −208
∴LHS = RHS
Por lo tanto, está probado.
Pregunta 9: Si 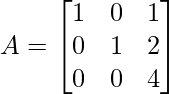 , entonces demuestra que ∣3A∣ = 27∣A∣.
, entonces demuestra que ∣3A∣ = 27∣A∣.
Solución:
Evalúa a lo largo de la primera columna,
Ahora cada elemento con 3,
= 3(36−0) − 0 + 0
= 108
Ahora, de acuerdo con la pregunta,
∣3A∣ = 27∣A∣
Sustituyendo los valores obtenemos,
108 = 27(4)
108 = 108
Por lo tanto , demostrado.
Pregunta 10: Encuentra los valores de x, si:
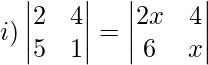
Solución:
2−20 = 2x 2 −24
−18 = 2x 2 −24
2x 2 = 6
Tomando la raíz cuadrada,
x 2 = 3
x = ±√3

Solución:
2 × 5 − 3 × 4 = 5 × x − 3 × 2x
10 − 12 = 5x − 6x
−2 = −x
x = 2
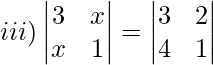
Solución:
3(1)−x(x) = 3(1)−2(4)
3−x 2 = 3−8
−x 2 = −8
x 2 = 8
x = ±
2√2
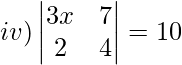
Solución:
3x(4)−7(2) = 10
12x−14 = 10
12x = 24
x = 24/12
x = 2
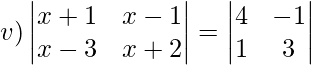
Solución:
Multiplicación cruzada de elementos de LHS,
(x+1)(x+2)−(x−3)(x−1) = 12+1
x 2 + 3x + 2 − x 2 +4x − 3 = 13
7x−1 = 13
7x = 14x
= 2
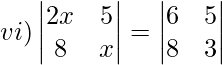
Solución:
2x(x)−5(8) = 6(3)−5(8)
2x 2 −40 = 18−40
2x 2 = 18
x 2 = 9
x = ±3
Pregunta 11: Encuentra el valor integral de x, si
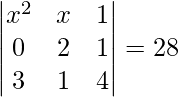
Solución:
Aquí tenemos que tomar el determinante de la array de 3×3
x 2 (8−1)−x(0−3)+1(0−6)
8x 2 −x 2 +3x−6 = 28
7x 2 +3x− 6 = 28
7x 2 +3x−34 = 0
Al factorizar la ecuación anterior obtenemos,
(7x+17)(x−2) = 0
x = 2
El valor integral de x es 2. Por lo tanto, x = −17/7 es no un entero.
Pregunta 12: ¿Para qué valor de x la array A es singular?
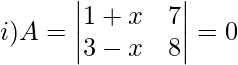
Solución:
La array A es singular si,
∣A∣ = 0
Cruz−multiplica los elementos en el determinante,
8 + 8x − 21 + 7x = 0
15x − 13 = 0
15x = 13
x = 13/15
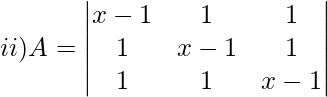
Solución:
La array A es singular si ∣A∣=0
Expandiendo a lo largo de la primera fila,
∣A∣ = (x−1)[(x−1) 2 −1] − 1[x−1−1] + 1[1−x+1]
∣A∣ = (x−1)(x 2 + 1−2x−1) − 1(x−2) + 1(2−x)Expandiendo los paréntesis para factorizar
|A| = (x−1)(x 2 −2x) − x + 2 + 2 − x
|A| = (x-1) × x × (x-2) + (4-2x)
|A| = (x−1)× x ×(x−2) + 2(2−x)
|A| = (x−1)× x ×(x−2) − 2(x−2)
[∴ Tomar (x−2) como común]
|A| = (x−2)[x(x−1)−2]
Como A es una array singular, entonces ∣A∣ = 0
(x−2)(x 2 −x−2) = 0
Hay dos casos,
Caso1 :
(x−2) = 0
x = 2
Caso2:
x 2 −x−2 = 0
x 2 −2x + x−2 = 0
x(x−2) + 1(x−2) = 0
(x−2 )(x+1) = 0
x = 2,−1
∴ x = 2 o −1