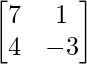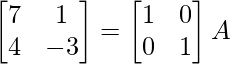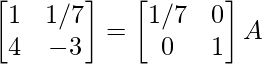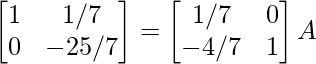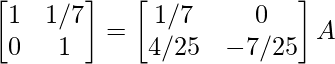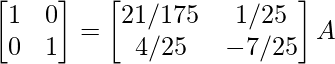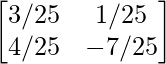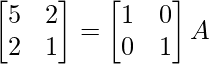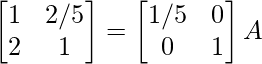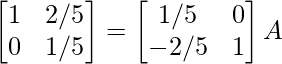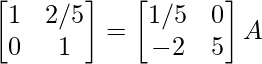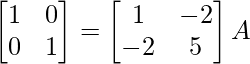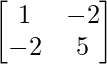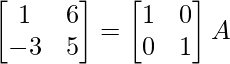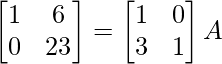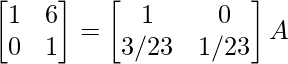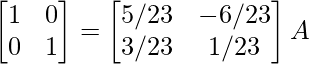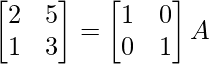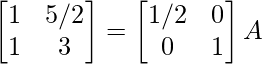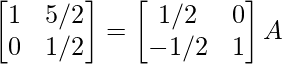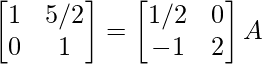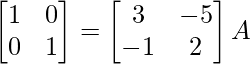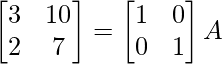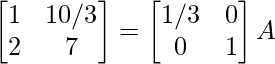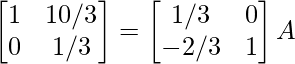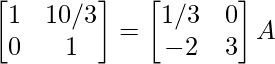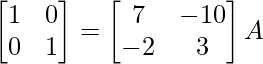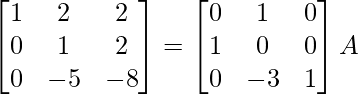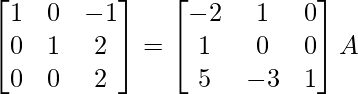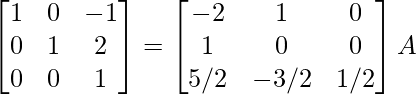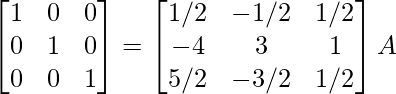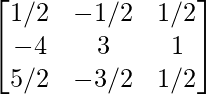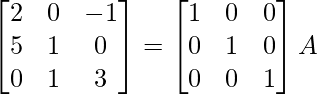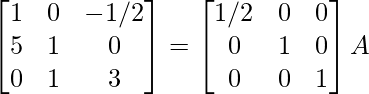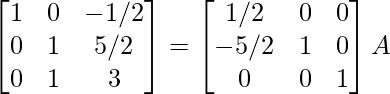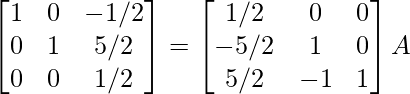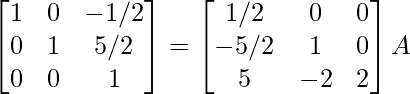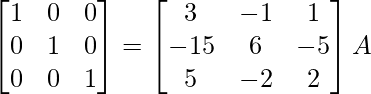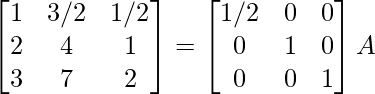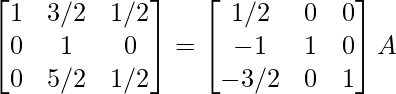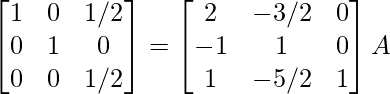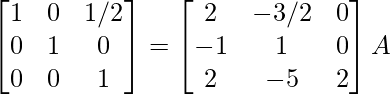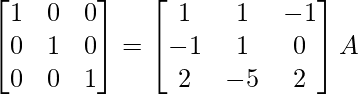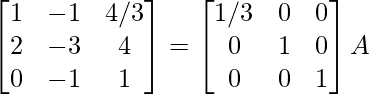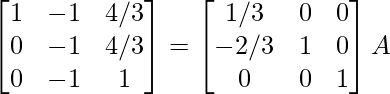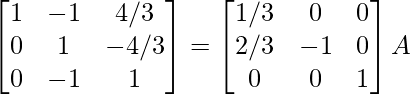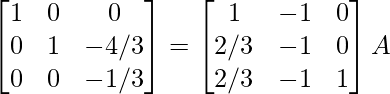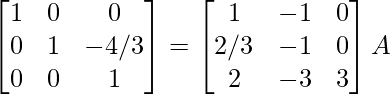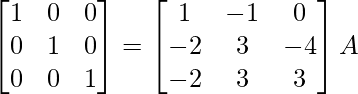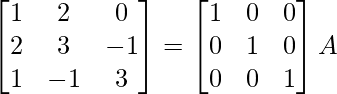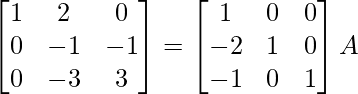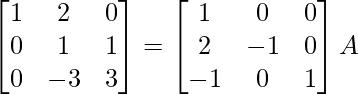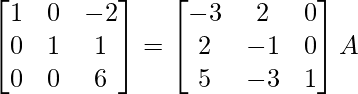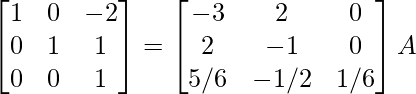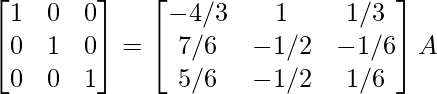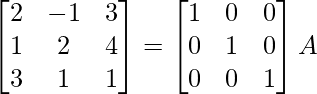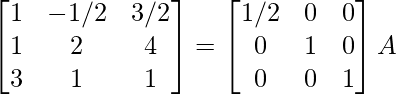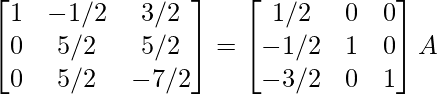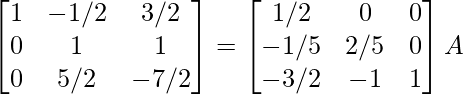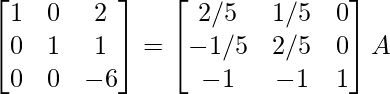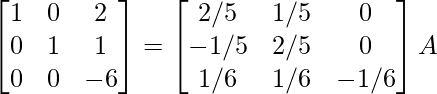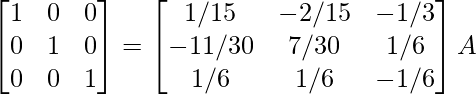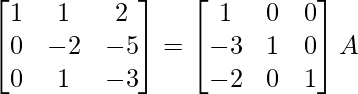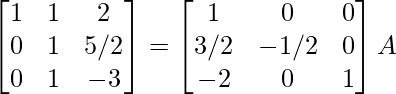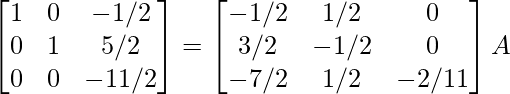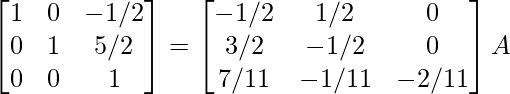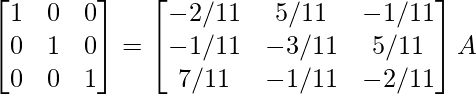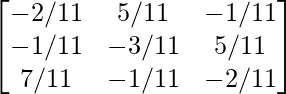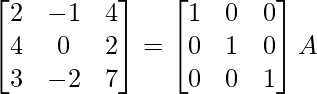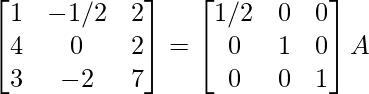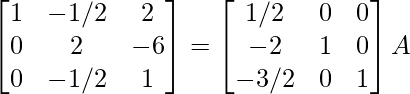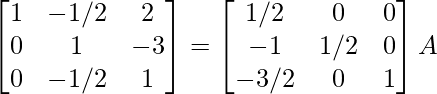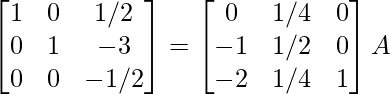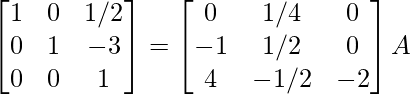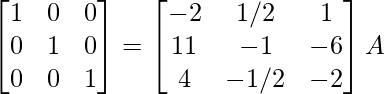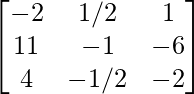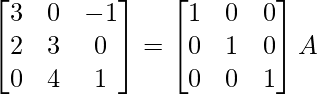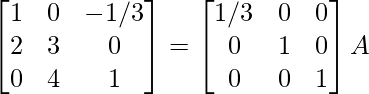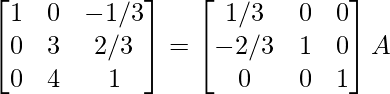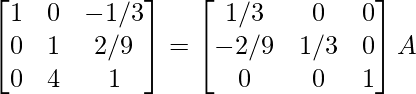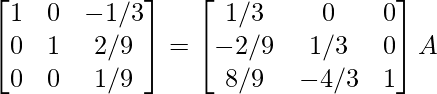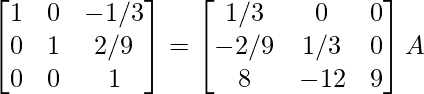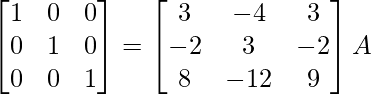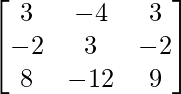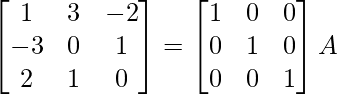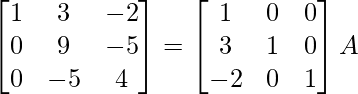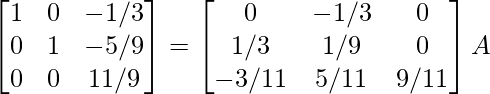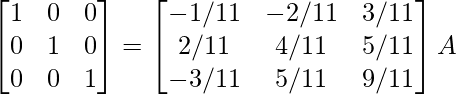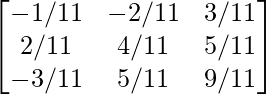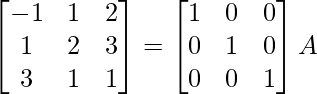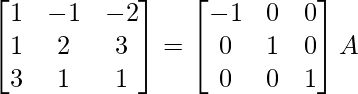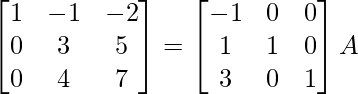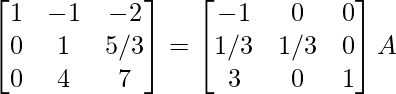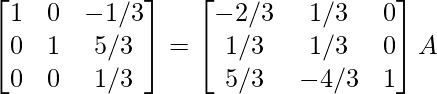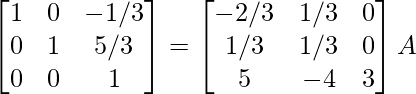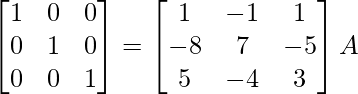Encuentre el inverso de cada una de las siguientes arrays utilizando la transformación de fila elemental (Preguntas 1-16):
Pregunta 1. 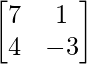
Solución:
Aquí, A =
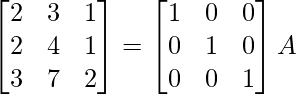
A = IA
Usando la operación de fila elemental
⇒
R 1 -> 1/7R 1
⇒
R 2 -> R 2 – 4R 1
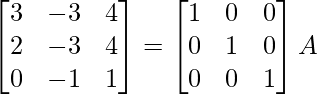
⇒
R2 – > (-7/25) R2
⇒
R 1 -> R 1 – 1/7R 2
⇒
Por lo tanto, A – 1 =
Pregunta 2. 
Solución:
Aquí, A =
A = IA
Usando la operación de fila elemental
⇒
R1 -> 1 / 5R1
⇒
R 1 -> R 2 – 2R 1
⇒
R2 – > 5R2
⇒
R 1 -> R 1 – 2/5R 2
⇒
Por lo tanto, A – 1 =
Pregunta 3. 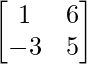
Solución:
Aquí, A =
A = IA
Usando la operación de fila elemental
⇒
R2 – > R2 + 3R1
⇒
R 2 -> 1/23R 2
⇒
R 1 -> R 1 – 6R 1
⇒
Por lo tanto, A – 1 =
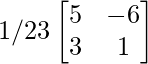
Pregunta 4. 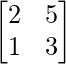
Solución:
Aquí,
A = IA
Usando la operación de fila elemental
⇒
R 1 -> 1/2R 1
⇒
R 2 -> R 2 – R 1
⇒
R2 – > 2R2
⇒
R 1 -> R 1 – 5/2R 2
⇒
Por lo tanto, A – 1 =
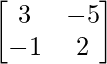
Pregunta 5. 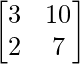
Solución:
Aquí, A =
A = IA
⇒
R 1 -> 1/3R 1
R 2 -> R 2 – 2R 1
R2 – > 3R2
R 1 -> R 1 – 10/3R 2
⇒
Por lo tanto, A – 1 =
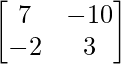
Pregunta 6. 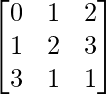
Solución:
Aquí, A =
A = IA
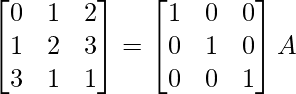
⇒
R 1 ↔ R 2
⇒
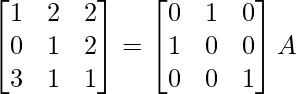
R 3 -> R 3 – 3R 1
⇒
R 1 -> R 1 – 2R 2 , R 3 -> R 3 + 5R 2
⇒
R 3 – > R 3/2
⇒
R 1 -> R 1 + R 3 , R 2 -> R 2 – 2R 3
⇒
Por lo tanto, A – 1 =
Pregunta 7. 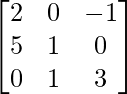
Solución:
Aquí, A =
A = IA
⇒
R 1 – > R 1/2
⇒
R 2 -> R 2 – 5R 1
⇒
R 3 -> R 3 – R 2
⇒
R 3 -> 2R 3
⇒
R 1 -> R 1 + 1/2R 3 , R 2 -> R 2 – 5/2R 3
⇒
Por lo tanto, A – 1 =
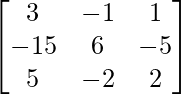
pregunta 8 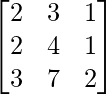
Solución:
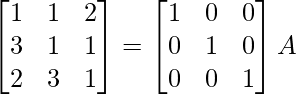
Aquí, A =
A = IA
⇒
R 1 -> 1/2R 1
⇒
R 2 -> R 2 – 2R 1 , R 3 -> R 3 – 3R 1
⇒
R 1 -> R 1 – 3/2R 2 , R 3 -> R 3 – 5/2R 2
⇒
R 3 -> 2R 3
⇒
R 1 -> R 1 – 1/2R 3
⇒
Por lo tanto, A – 1 =
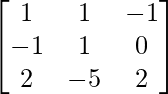
Pregunta 9. 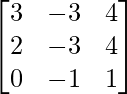
Solución:
Aquí, A =
A = IA
⇒
R 1 -> 1/3R 1
⇒
R 2 -> R 2 – 2R 1
⇒
R2 – > (-1) R2
⇒
R 1 -> R 1 + R 2 , R 3 -> R 3 + R 2
⇒
R3 -> (-3 ) R3
⇒
R2 -> R2 + 4 / 3R3
⇒
Por lo tanto, A – 1 =
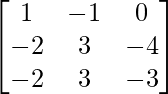
Pregunta 10. 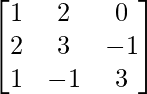
Solución:
Aquí, A =
⇒
R 2 -> R 2 – 2R 1 , R 3 -> R 3 – R 1
⇒
R2 – > (-1) R2
⇒
R 1 -> R 1 – 2R 2 , R 3 -> R 3 + 3R 2
⇒
R 3 – > R 3/6
⇒
R 1 -> R 1 + 2R 3 , R 2 -> R 2 – R 3
⇒
Por lo tanto, A – 1 =
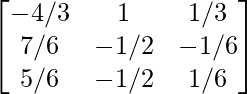
Pregunta 11. 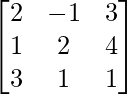
Solución:
Aquí, A =
A = IA
⇒
R 1 – > R 1/2
⇒
R 2 -> R 2 – R 1 , R 3 -> R 3 – 3R 1
⇒
R2 – > (2/5) R2
⇒
R 1 -> R 1 + 1/2 R 2 , R 3 -> R 3 – 5/2R 2
⇒
R 3 -> R 3 /-6
⇒
R 2 -> R 2 – R 3 , R 1 -> R 1 – 2R 3
⇒
Por lo tanto, A – 1 =
Pregunta 12. 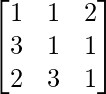
Solución:
Aquí, A =
A = IA
⇒
R 2 -> R 2 – 3R 1 , R 3 -> R 3 – 2R 1
⇒
R 2 -> R 2 /(-2)
⇒
R 1 -> R 1 – R 2 , R 3 -> R 3 – R 2
⇒
R 3 -> (-2/11)R 3
⇒
R 1 -> R 1 + 1/2R 3 , R 2 -> R 2 – 5/2R 3
⇒
Por lo tanto, A – 1 =
Pregunta 13. 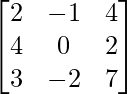
Solución:
Aquí, A =
A = IA
⇒
R 1 -> 1/2R 1
⇒
R 2 -> R 2 – 4R 1 , R 3 -> R 3 – 3R 1
⇒
R 2 -> 1/2R 2
⇒
R 1 -> R 1 + 1/2R 2 , R 3 -> R 3 + 1/2R 2
⇒
R3 -> (-2 ) R3
⇒
R 1 -> R 1 – 1/2R 3 , R 2 -> R 2 + 3R 3
⇒
Por lo tanto, A – 1 =
Pregunta 14. 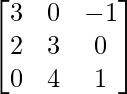
Solución:
Aquí, A =
A = IA
⇒
R1 -> (1/3 ) R1
⇒
R 2 -> R 2 – 2R 1
⇒
R2 – > (1/3) R2
⇒
R 3 -> R 3 – 4R 2
⇒
R 3 -> 9R 3
⇒
R 1 -> R 1 + 1/3R 3 , R 2 -> R 2 – 2/9R 3
⇒
Por lo tanto, A – 1 =
Pregunta 15. 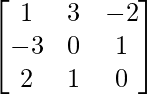
Solución:
Aquí, A =
A = IA
⇒
R 2 -> 3R 1 + R 2 , R 3 -> R 3 – 2R 1
⇒
R 1 -> R 1 – 3R 2 , R 3 -> R 3 + 5R 2
⇒
R 2 -> R 2 + 5/9R 3 , R 1 -> R 1 + 1/3R 3
⇒
Por lo tanto, A – 1 =
Pregunta 16. 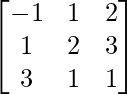
Solución:
Aquí, A=
A = IA
⇒
R1 -> (-1 ) R1
⇒
R 2 -> R 2 – R 1 , R 3 -> R 3 – 3R 1
⇒
R 2 – > R 2/3
⇒
R 1 -> R 1 + R 2 , R 3 -> R 3 – 4R 2
⇒
R 3 -> R 3 /3
⇒
R 1 -> R 1 + 1/3R 3 , R 2 -> R 2 – 5/3R 3
⇒
Por lo tanto, A – 1 =
Publicación traducida automáticamente
Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA