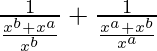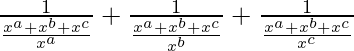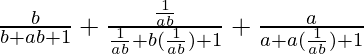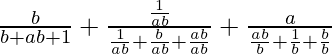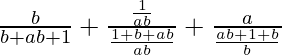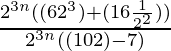Pregunta 1 (i). Simplifica 3(a 4 b 3 ) 10 × 5(a 2 b 2 ) 3
Solución:
Dado 3(a 4 b 3 ) 10 × 5(a 2 b 2 ) 3
= 3 × un 40 × segundo 30 × 5 × un 6 × segundo 6
= 3 × un 46 × segundo 36 × 5 [un metro × un norte = un metro+ n ]
= 15 × a 46 × b 36
= 15a 46 b 36
Por lo tanto, 3(a 4 b 3 ) 10 × 5(a 2 b 2 ) 3 = 15a 46 b 36
Pregunta 1 (ii). Simplifica (2x -2 y 3 ) 3
Solución:
Dado (2x -2 y 3 ) 3
= 2 3 × x -6 × y 9
= 8 × x -6 × y 9 [un metro × un norte =un metro+ n ]
= 8x -6 y 9
Así, (2x -2 y 3 ) 3 = 8x -6 y 9
Pregunta 1 (iii). Simplificar 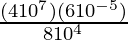
Solución:
Dado
=
=
[un metro × un norte = un metro+ n ]
=
= 3/10 2
= 3/100
De este modo,
Pregunta 1 (iv). Simplificar 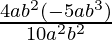
Solución:
Dado
=
=
=
[un metro × un norte = un metro+ n ]
= -2×a 2 ×b 5 ×a -2 ×b -2
= -2×a 2+(-2) ×b 5+(-2) [un metro × un norte = un metro+ n ]
= -2×a 0 ×b 3
= -2b 3 [a 0 =1]
Por lo tanto,
=-2b 3
Pregunta 1 (v). Simplificar 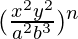
Solución:
Dado
=
=
[un metro × un norte = un metro+ n ]
De este modo,
Pregunta 1 (vi). Simplificar 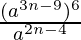
Solución:
Dado
=
[(un metro ) norte = un mn ]
=
= un 18n-54 × un -(2n-4) [ un metro × un norte = un metro + n ]
= un 18n-54-2n+4
= un 16n-50
Así,
= a 16n-50
Pregunta 2 (i) Si a = 3 y b = -2, encuentre el valor de a a + b b
Solución:
Dado a = 3 y b = -2
Al sustituir el valor de a y b en a a + b b , obtenemos
una una + segundo segundo = 3 3 + (-2) -2
= 27 + 1/4
= (108 + 1)/4
= 109/4
Así, a a + b b = 109/4
Pregunta 2 (ii). Si a = 3 y b = -2, encuentre el valor de a b + b a
Solución:
Dado a = 3 y b = -2
Al sustituir el valor de a y b en a b + b a , obtenemos
un segundo + segundo un = 3 -2 + (-2) 3
= 1/9 + (-8)
= (1 – 72)/9
= -71/9
Así, a b + b a = -71/9
Pregunta 2 (iii). Si a = 3 y b = -2, encuentre el valor de (a + b) ab .
Solución:
Dado a = 3 y b = -2
Al sustituir el valor de a y b en (a + b) ab , obtenemos
(a + b) ab = (3 + (-2)) 3×-2
= (1) -6
= 1
Así, (a + b) ab = 1
Pregunta 3 (i). Pruebalo 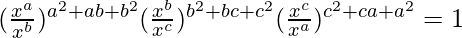
Solución:
Primero resolvamos el lado izquierdo de la ecuación dada
Usando la fórmula (a m ) n = a mn , obtenemos
=
Usando la fórmula a m /a n = a m-n , obtenemos
=
=
=
Usando la fórmula a m × a n = a m+n , obtenemos
=
= x
= 1
= Lado derecho de la ecuación dada
Así, probamos que
Pregunta 3 (ii). Pruebalo 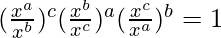
Solución:
Consideremos el lado izquierdo de la ecuación dada
Usando la fórmula, (a m ) n = a mn , obtenemos
=
=
=
[un metro × un norte = un metro+ n ]
= 1
= Lado derecho de la ecuación dada
Así, probamos que
Pregunta 3 (iii). Pruebalo 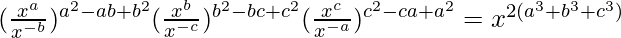
Solución:
Primero resolvamos el lado izquierdo de la ecuación dada
Usando la fórmula (a m ) n = a mn , obtenemos
=
Usando la fórmula a m /a n = a m-n , obtenemos
=
=
=
Usando la fórmula a m × a n = a m+n , obtenemos
=
=
= Lado derecho de la ecuación dada
Así, probamos que
Pregunta 4 (i). Pruebalo 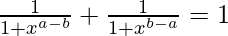
Solución:
Consideremos primero el lado izquierdo de la ecuación dada
=
=
=
=
= 1
= Lado derecho de la ecuación dada
Así, probamos que
Pregunta 4 (ii). Pruebalo 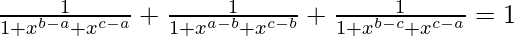
Solución:
Consideremos primero el lado izquierdo de la ecuación dada
=
=
=
=
= 1
= Lado derecho de la ecuación dada
Así, probamos que
Pregunta 5 (i). Pruebalo 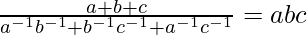
Solución:
Consideremos primero el lado izquierdo de la ecuación dada
=
=
= abc
= Lado derecho de la ecuación dada
Así, probamos que
Pregunta 5 (ii). Pruebalo 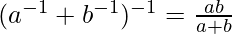
Solución:
Consideremos primero el lado izquierdo de la ecuación dada
=
=
=
=
= Lado derecho de la ecuación dada
Así, probamos que
Pregunta 6. Si abc = 1, demuestre que 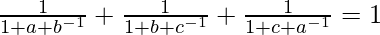
Solución:
Dado abc = 1
⇒ c = 1/ab
Consideremos primero el lado izquierdo de la ecuación dada
=
=
=
Sustituyendo el valor de c en la ecuación anterior, obtenemos
=
=
=
=
=
= 1
= Lado derecho de la ecuación dada
Así, hemos demostrado que si abc = 1,
Pregunta 7 (i). Simplificar 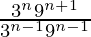
Solución:
Dado
=
=
=
[un metro × un norte = un metro+ n ]
=
= 3 3n+2-(3n-3) [un metro /un norte = un metro- n ]
= 3 5
= 243
Por lo tanto,
= 243
Pregunta 7 (ii). Simplificar 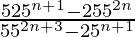
Solución:
Dado
=
=
=
[un metro × un norte = un metro+ n ]
=

= 4/24
= 1/6
Por lo tanto,
= 1/6
Pregunta 7 (iii). Simplificar 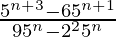
Solución:
Dado,
=
=
= (19 × 5)/5
= 19
De este modo,
Pregunta 7 (iv). Simplificar 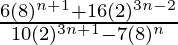
Solución:
Dado
=
=
=
=
=
= (48 + 4)/13
= 52/13
= 4
De este modo,
Pregunta 8 (i). Resuelva la ecuación 7 2x+3 = 1 para x.
Solución:
Dada la ecuación 7 2x+3 = 1
Sabemos que, para cualquier número a∈ Real, a 0 = 1
Sea a = 7
⇒ 7 2x+3 = 7 0
Como las bases son iguales, igualemos los exponentes
⇒ 2x + 3 = 0
⇒ x = -3/2
Por lo tanto, el valor de x es -3/2
Pregunta 8 (ii). Resuelva la ecuación 2 x+1 = 4 x-3 para x.
Solución:
Dado 2 x+1 = 4 x-3
Podemos escribir 4 = 2 2
⇒ 2x+1 =2 2(x-3)
⇒ 2x +1 = 2 2x-6
Como las bases son iguales, igualemos los exponentes
⇒ x + 1 = 2x – 6
⇒ x = 7
Por lo tanto, el valor de x es 7
Pregunta 8 (iii). Resuelva la ecuación 2 5x+3 = 8 x+3 para x.
Solución:
Dado 2 5x+3 = 8 x+3
Sabemos que 8 = 2 3
⇒ 2 5x+3 = 2 3(x+3)
⇒ 2 5x+3 = 2 3x+9
Como las bases son iguales, igualemos los exponentes
⇒ 5x + 3 = 3x + 9
⇒ 5x – 3x = 9 – 3
⇒ 2x = 6
⇒ x = 3
Por lo tanto, el valor de x es 3
Pregunta 8 (iv). Resuelve la ecuación 4 2x = 1/32 para x.
Solución:
Dado 4 2x = 1/32
⇒ 2 2(2x) = 1/32
⇒ 2 2(2x) × 32 = 1
⇒ 2 4x × 2 5 = 1
⇒ 2 4x+5 = 2 0
Como las bases son iguales, igualemos los exponentes
⇒ 4x + 5 = 0
⇒ x = -5/4
Por lo tanto, el valor de x es -5/4
Pregunta 8 (v). Resuelve la ecuación 4 x – 1 × (0.5) 3-2x = (1/8) x para x.
Solución:
Dado 4 x – 1 × (0.5) 3-2x = (1/8) x
⇒
⇒
⇒ 2 2(x-1) × 2 -(3-2x) = 2 -3x
⇒ 2 2x-2-3+2x = 2 -3x
⇒ 2 4x-5 = 2 -3x
Como las bases son iguales, igualemos los exponentes
⇒ 4x – 5 = -3x
⇒ 7x = 5
⇒ x = 5/7
Por lo tanto, el valor de x es 5/7
Pregunta 8 (vi). Resuelve la ecuación 2 3x-7 = 256 para x.
Solución:
Dado 2 3x-7 = 256
⇒ 2 3x-7 = 2 8
Como las bases son iguales, igualemos los exponentes
⇒ 3x – 7 = 8
⇒ x = 15/3
⇒ x = 5
Por lo tanto, el valor de x es 5
Pregunta 9 (i). Resuelva la ecuación 2 2x – 2 x+3 + 2 4 = 0 para x.
Solución:
Dado 2 2x – 2 x+3 + 2 4 = 0
⇒ (2 x ) 2 – 2 × 2 x × 2 2 + (2 2 ) 2 = 0
⇒ (2 x – 2 2 ) 2 = 0
⇒ 2 x – 2 2 = 0
⇒ 2 x = 2 2
Como las bases son iguales, igualemos los exponentes
⇒ x = 2
Por lo tanto, el valor de x es 2
Pregunta 9 (ii). Resuelve la ecuación 3 2x+4 + 1 = 2.3 x+2 para x.
Solución:
Dado 3 2x+4 + 1 = 2.3 x+2
⇒
⇒
⇒ ( 3x+2 – 1) 2 = 0
⇒ 3x+2 – 1 = 0
⇒ 3x+2 = 3 0
Como las bases son iguales, igualemos los exponentes
⇒ x + 2 = 0
⇒ x = -2
Por lo tanto, el valor de x es -2
Pregunta 10. Si 49392 = a 4 b 2 c 3 , encuentre los valores de a, b y c donde a, b y c son números primos positivos diferentes.
Solución:
Primero averigüemos la descomposición en factores primos de 49392
Por lo tanto, 49392 = 2 4 × 3 2 × 7 3
Donde 2, 3 y 7 son primos positivos
49392 = 2 4 3 2 7 3 = un 4 segundo 2 do 3
Así, al comparar, obtenemos
a = 2, b = 3 y c = 7
Así, los valores de a, b y c son 2, 3, 7 respectivamente.
Pregunta 11. Si 1176 = 2 a 3 b 7 c , encuentra a, b y c.
Solución:
Dado 1176 = 2 a 3 b 7 c
Primero averigüemos la descomposición en factores primos de 1176
Por lo tanto, 1176 = 2 3 × 3 1 × 7 2
1176 = 2 3 3 1 7 2 = 2 un 3 segundo 7 c
Así, al comparar, obtenemos
a = 3, b = 1, c = 2
Así, los valores de a, b y c son 3, 1, 2 respectivamente.
Pregunta 12. Dado 4725 = 3 a 5 b 7 c , encuentra
(i) los valores integrales de a, b y c
(ii) el valor de 2 -a 3 b 7 c
Solución:
Dado 4725 = 3 a 5 b 7 c
(i) Averigüemos primero la descomposición en factores primos de 4725
Por lo tanto, 4725 = 3 3 × 5 2 × 7 1
4725 = 3 3 5 2 7 1 = 3 un 5 segundo 7 c
Así, al comparar, obtenemos
a = 3, b = 2, c = 1
Así, los valores de a, b y c son 3,2,1 respectivamente.
(ii) Aquí a = 3, b = 2, c = 1
Al sustituir estos valores en 2 -a 3 b 7 c
2 -a 3 b 7 c = 2 -3 ×3 2 ×7 1
= 1/8 × 9 × 7 = 63/8
Por lo tanto, el valor de 2 -a 3 b 7 c es 63/8
Pregunta 13. Si a = xy p-1 , b = xy q-1 , c = xy r-1 , demuestre que a q-r b r-p c p-q = 1.
Solución:
Dado a = xy p-1 , b = xy q-1 , c = xy r-1
a q-r b r-p c p-q =
=
= x q-r+r-p+pq y (p-1)(qr)+(rp)(q-1)+(pq)(r-1)
= x q-r+r-p+pq y pq-q-pr+r+rq-r-pq+p+pr-p-qr+q
= x 0 y 0
= 1
Así, demostramos que a q-r b r-p c p-q = 1
Publicación traducida automáticamente
Artículo escrito por prasanthinidamarthy y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA