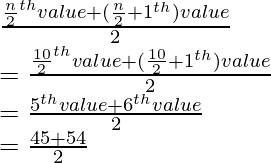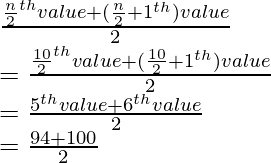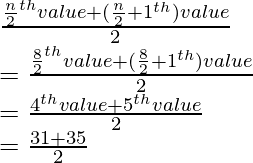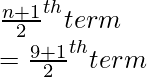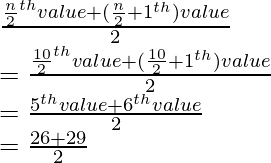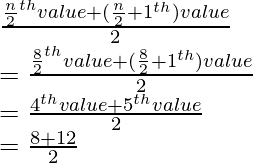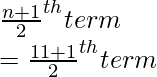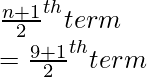Clase 9 RD Sharma Solutions – Capítulo 24 Medidas de Tendencia Central – Ejercicio 24.3

Pregunta 1. Encuentra la mediana de los siguientes datos:

83, 37, 70, 29, 45, 63, 41, 70, 34, 54

Solución:

Secuencia en orden ascendente de los números:

29, 34, 37, 41, 45, 54, 63, 70, 70, 83

Número total de términos, supuestamente, n = 10 (par)

mediana =

$\\ \frac{\frac{n}{2}^{th} \space value + (\frac{n}{2}+1\space ^{th}) value}{2} \\ = \frac{\frac{10}{2}^{th} \space value + (\frac{10}{2}+1\space ^{th}) value}{2} \\ = \frac{5^{th} value+ 6^{th} value}{2} \\ = \frac{45+54}{2}$

= 99/2

= 49,5

Pregunta 2. Encuentra la mediana de los siguientes datos:

133, 73, 89, 108, 94, 104, 94, 85, 100, 120

Solución:

Secuencia en orden ascendente de los números:

73, 85, 89, 94, 94, 100, 104, 108, 120, 133

Número total de términos, supuestamente, n = 10 (par)

mediana =

$\\ \frac{\frac{n}{2}^{th} \space value + (\frac{n}{2}+1\space^{th}) value}{2} \\ = \frac{\frac{10}{2}^{th} \space value + (\frac{10}{2}+1\space ^{th}) value}{2} \\ = \frac{5^{th} value+ 6^{th} value}{2} \\ = \frac{94+100}{2}$

= 194/2

= 97

Pregunta 3. Encuentra la mediana de los siguientes datos:

31, 38, 27, 28, 36, 25, 35, 40

Solución:

Secuencia en orden ascendente de los números:

25, 27, 28, 31, 35, 36, 38, 40

Número total de términos, supuestamente, n = 8 (par)

mediana =

$\\ \frac{\frac{n}{2}^{th} \space value + (\frac{n}{2}+1\space ^{th}) value}{2} \\ = \frac{\frac{8}{2}^{th} \space value + (\frac{8}{2}+1\space ^{th}) value}{2} \\ = \frac{4^{th} value+ 5^{th} value}{2} \\ = \frac{31+35}{2}$

= 66/2

= 33

Pregunta 4. Encuentra la mediana de los siguientes datos:

15, 6, 16, 8, 22, 21, 9, 18, 25

Solución:

Secuencia en orden ascendente de los números:

6, 8, 9, 15, 16, 18, 21, 22, 25

Número total de términos, supuestamente, n = 9 (impar)

mediana =

$\\ \frac{n+1}{2}^{th} term \\ = \frac{9+1}{2}^{th} term$

= ^5to término

= 16

Pregunta 5. Encuentra la mediana de los siguientes datos:

41, 43, 127, 99, 71, 92, 71, 58, 57

Solución:

Secuencia en orden ascendente de los números:

41, 43, 57, 58, 71, 71, 92, 99, 127

Número total de términos, supuestamente, n = 9 (impar)

mediana =

$\\ \frac{n+1}{2}^{th} term \\ = \frac{9+1}{2}^{th} term$

= ^5to término

= 71

Pregunta 6. Encuentra la mediana de los siguientes datos:

25, 34, 31, 23, 22, 26, 35, 29, 20, 32

Solución:

Secuencia en orden ascendente de los números:

20, 22, 23, 25, 26, 29, 31, 32, 34, 35

Número total de términos, supuestamente, n = 10 (par)

mediana =

$\\ \frac{\frac{n}{2}^{th} \space value + (\frac{n}{2}+1\space ^{th}) value}{2} \\ = \frac{\frac{10}{2}^{th} \space value + (\frac{10}{2}+1\space ^{th}) value}{2} \\ = \frac{5^{th} value+ 6^{th} value}{2} \\ = \frac{26+29}{2}$

= 55/2

= 27,5

Pregunta 7. Encuentra la mediana de los siguientes datos:

12, 17, 3, 14, 5, 8, 7, 15

Solución:

Secuencia en orden ascendente de los números:

3, 5, 7, 8, 12, 14, 15, 17

Número total de términos, supuestamente, n = 8 (par)

mediana =

$\\ \frac{\frac{n}{2}^{th} \space value + (\frac{n}{2}+1\space^{th}) value}{2} \\ = \frac{\frac{8}{2}^{th} \space value + (\frac{8}{2}+1\space ^{th}) value}{2} \\ = \frac{4^{th} value+ 5^{th} value}{2} \\ = \frac{8+12}{2}$

= 20/2

= 10

Pregunta 8. Encuentra la mediana de los siguientes datos:

92, 35, 67, 85, 72, 81, 56, 51, 42, 69

Solución:

Secuencia en orden ascendente de los números:

35, 42, 51, 56, 67, 69, 72, 81, 85, 92

Número total de términos, supuestamente, n = 10 (par)

mediana =

$\\ \frac{\frac{n}{2}^{th} \space value + (\frac{n}{2}+1\space ^{th}) value}{2} \\ = \frac{\frac{10}{2}^{th} \space value + (\frac{10}{2}+1\space ^{th}) value}{2} \\ = \frac{5^{th} value+ 6^{th} value}{2} \\ = \frac{67+69}{2}$

= 136/2

= 68

Pregunta 9. Los números 50, 42, 35, 2x + 10, 2x – 8, 12, 11, 8 están escritos en orden descendente y su mediana es 25, encuentra x.

Solución:

Secuencia en orden ascendente de los números:

8, 11, 12, 2x – 8, 2x+10, 35, 42, 50

Número total de términos, supuestamente, n = 8 (par)

Dado,

mediana = 25

mediana =

$\\ \frac{\frac{n}{2}^{th} \space value + (\frac{n}{2}+1\space ^{th}) value}{2} \\ 25 = \frac{\frac{8}{2}^{th} \space value + (\frac{8}{2}+1\space ^{th}) value}{2} \\25 = \frac{4^{th} value+ 5^{th} value}{2} \\25 = \frac{2x-8 + 2x+10}{2} \\25= \frac{4x+2}{2}$

48 = 4x

X = 12

Pregunta 10. Encuentra la mediana de las siguientes observaciones: 46, 64, 87, 41, 58, 77, 35, 90, 55, 92, 33. Si 92 se reemplaza por 99 y 41 por 43 en los nuevos datos, encuentra el nueva mediana?

Solución:

Secuencia en orden ascendente de los números:

33, 35, 41, 46, 55, 58, 64, 77, 87, 90, 92

n = 11 (impar)

mediana =

$\\ \frac{n+1}{2}^{th} term \\ = \frac{11+1}{2}^{th} term$

= 6 ^° término

= 58

Si reemplazamos 92 por 99 y 41 y 43, entonces la nueva secuencia de números es:

33, 35, 43, 46, 55, 58, 64, 77, 87, 90, 99

Nueva mediana =

$\\ \frac{n+1}{2}^{th} term \\ = \frac{11+1}{2}^{th} term$

= 6 ^° término

= 58

Pregunta 11. Encuentra la mediana de los siguientes datos: 41, 43, 127, 99, 61, 92, 71, 58, 57. Si se reemplaza 58 por 85, ¿cuál será la nueva mediana?

Solución:

Ordenando los datos dados en orden ascendente:

41, 43, 57, 58, 61, 71, 92, 99, 127

Número de términos, supuestamente n = 9 (impar)

mediana =

$\\ \frac{n+1}{2}^{th} term \\ = \frac{9+1}{2}^{th} term$

= ^5to término

= 61

Al reemplazar el valor 58 por 85, obtenemos,

41, 43, 57, 61, 71, 85, 92, 99, 127

Nueva mediana =

$\\ \frac{n+1}{2}^{th} term \\ = \frac{9+1}{2}^{th} term$

= ^5to término

= 71

Pregunta 12. Los pesos (en kg) de 15 alumnos son: 31, 35, 27, 29, 32, 43, 37, 41, 34, 28, 36, 44, 45, 42,30. Encuentre la mediana en peso. Si se sustituyen los 44 kg por 446 kg y los 27 kg por 25 kg. Encuentre la nueva mediana.

Solución :

Ordenando los datos en orden ascendente,

27, 28, 29, 30, 31, 32, 34, 35, 36, 37, 41, 42, 43, 44, 45

Número total de términos = 15 (n = impar)

mediana =

$\\ \frac{n+1}{2}^{th} term \\ = \frac{15+1}{2}^{th} term$

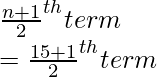
= ^8vo término

= 35kg

Al reemplazar 44 kg por 46 kg y 27 kg por 25 kg respectivamente, obtenemos,

25, 28, 29, 30, 31, 32, 34, 35, 36, 37, 41, 42, 43, 45,46

Nueva mediana =

$\\ \frac{n+1}{2}^{th} term \\ = \frac{15+1}{2}^{th} term$

= ^8vo término

= 35kg

Pregunta 13. Las siguientes observaciones se han ordenado en orden ascendente. Si la mediana de los datos es 63, encuentra el valor de x.

29, 32, 48, 50, x, x + 2, 72, 78, 84, 95

Solución :

Dado,

mediana = 63

Número total de términos, supuestamente n = 10 (par)

Ahora,

mediana =

$\\ \frac{\frac{n}{2}^{th}\space term + (\frac{n}{2}+1^{th}) term}{2} \\ 63 = \frac{\frac{10}{2}^{th}\space term + (\frac{10}{2}+1^{th}) term}{2} \\ 63 = \frac{5^{th} + 6^{th} term}{2} \\ 63 = \frac{x+x+2}{2} \\ 63 =\frac{2x+2}{2}$

63 = x+1

x = 62

Publicación traducida automáticamente

Artículo escrito por yashkumar0457 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Encuentra la mediana de los siguientes datos:

83, 37, 70, 29, 45, 63, 41, 70, 34, 54

Pregunta 2. Encuentra la mediana de los siguientes datos:

133, 73, 89, 108, 94, 104, 94, 85, 100, 120

Pregunta 3. Encuentra la mediana de los siguientes datos:

31, 38, 27, 28, 36, 25, 35, 40

Pregunta 4. Encuentra la mediana de los siguientes datos:

15, 6, 16, 8, 22, 21, 9, 18, 25

Pregunta 5. Encuentra la mediana de los siguientes datos:

41, 43, 127, 99, 71, 92, 71, 58, 57

Pregunta 6. Encuentra la mediana de los siguientes datos:

25, 34, 31, 23, 22, 26, 35, 29, 20, 32

Pregunta 7. Encuentra la mediana de los siguientes datos:

12, 17, 3, 14, 5, 8, 7, 15

Pregunta 8. Encuentra la mediana de los siguientes datos:

92, 35, 67, 85, 72, 81, 56, 51, 42, 69

Pregunta 9. Los números 50, 42, 35, 2x + 10, 2x – 8, 12, 11, 8 están escritos en orden descendente y su mediana es 25, encuentra x.

Pregunta 10. Encuentra la mediana de las siguientes observaciones: 46, 64, 87, 41, 58, 77, 35, 90, 55, 92, 33. Si 92 se reemplaza por 99 y 41 por 43 en los nuevos datos, encuentra el nueva mediana?

Pregunta 11. Encuentra la mediana de los siguientes datos: 41, 43, 127, 99, 61, 92, 71, 58, 57. Si se reemplaza 58 por 85, ¿cuál será la nueva mediana?

Pregunta 12. Los pesos (en kg) de 15 alumnos son: 31, 35, 27, 29, 32, 43, 37, 41, 34, 28, 36, 44, 45, 42,30. Encuentre la mediana en peso. Si se sustituyen los 44 kg por 446 kg y los 27 kg por 25 kg. Encuentre la nueva mediana.

Pregunta 13. Las siguientes observaciones se han ordenado en orden ascendente. Si la mediana de los datos es 63, encuentra el valor de x.

29, 32, 48, 50, x, x + 2, 72, 78, 84, 95

Deja una respuesta Cancelar la respuesta