Las integrales indefinidas son el reverso del proceso de diferenciación. Dada una función f(x) y su derivada f'(x), nos ayudan a calcular la función f(x) a partir de f'(x). Estos se utilizan en casi todas partes en el cálculo y, por lo tanto, se denominan la columna vertebral del campo del cálculo. Hablando geométricamente, las integrales representan el área y el volumen bajo la curva. A menudo, las curvas son complicadas y las fórmulas para el volumen y las áreas solo están disponibles para un puñado de curvas. En esos casos, se hace necesario aprender la forma generalizada de calcular las áreas y el volumen de formas arbitrarias.
Integrales indefinidas
Para calcular las integrales es fundamental saber calcular las antiderivadas de una función. Una antiderivada de la función f(x) es una función cuya derivada es igual a f(x). Es decir, si F'(x) = f(x), la F(x) se llamará la antiderivada de la función f(x). Además, se debe tener en cuenta que las antiderivadas no son únicas, una función puede tener infinitas antiderivadas. Una integral se denota con el signo ∫.
F'(x) = f(x),
F(x) = ∫f(x) + C
Donde C, es una constante arbitraria.
El símbolo ∫ se llama símbolo integral, la función f(x) se llama integrada y x se llama variable de integración.
Propiedades de Integración
Propiedad 1: ∫kf(x)dx= k∫f(x)dx
Propiedad 2: ∫f(x)± g(x)dx= ∫f(x)dx± ∫g(x)dx
Propiedad 3: ∫(f 1 (x)dx± f 2 (x)dx± f 3 (x)dx….)= ∫f 1 (x)dx± ∫f 2 (x)± ∫f 3 (x) dx…
Integrales de funciones comunes
Las integrales de funciones comunes se pueden inferir directamente de sus derivadas solamente. Es esencial recordar las antiderivadas para estas funciones estándar. Facilita el cálculo de las integrales, que suelen ser una combinación de algunas funciones estándar. Por ejemplo, para la función F(x), y su derivada f(x). Esto se puede reescribir como,
F'(x) = f(x)
F(x) = ∫f(x) + C
Por ejemplo,
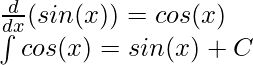
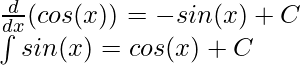
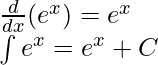
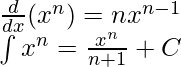
La regla anterior no se aplica cuando x = -1,
![]()
Estas funciones y sus integrales se pueden resumir en la siguiente tabla:
| Función | Integral |
| x norte | |
| pecado(x) | -cos(x) |
| porque(x) | pecado(x) |
| e x | e x |
| segundo 2 (x) | bronceado(x) |
| en(x) |
Soluciones Particulares a la Ecuación Diferencial – Función Racional
Por lo general, a las constantes no se les da tanta importancia. Pero en algunos casos, se vuelve importante cuándo. Por ejemplo, considere la función dada f'(x) = ![]() . Se da que f(2) = 12. El objetivo es encontrar f(-1).
. Se da que f(2) = 12. El objetivo es encontrar f(-1).
Reescribamos las funciones dadas,
f(x) = ∫f'(x) = ∫x -3 = -12x 2 + C
Se da que,
f(2) = 12
⇒ -12(2) 2 + C = 12
⇒ C = 60
Reemplazando el valor de C en la ecuación de f(x),
f(x) = -12x 2 + 60
f(-1) = -12(-1) 2 + 60
f(-1) = 48
Soluciones Particulares a la Ecuación Diferencial – Función Exponencial
El caso anterior era para funciones racionales. Esta vez, consideremos el caso similar de las funciones exponenciales. Considere la función f'(x) = 5e x , Se da que f(7) = 40 + 5e 7 , El objetivo es encontrar el valor de f(5). Reescribiendo las funciones dadas,
f(x) = ∫f'(x) = ∫5e x = 5e x + C
Se da que,
f(7) = 5e 7 + C
⇒40 + 5e 7 = 5e 7 + C
⇒ C = 40
f(x) = 5ex + 40
⇒f(5) = 5e 5 + 40
Veamos algunos ejemplos de problemas con estos conceptos.
Problemas de muestra
Pregunta 1: Encuentra la integral para la función dada f(x),
f(x) = sen(x) + 2
Solución:
Dado f(x) = sen(x) + 2
sin(x) es una función estándar y se conoce su antiderivada.
∫f(x)dx
⇒ ∫(sen(x) + 2)dx
Usando la propiedad 2 mencionada anteriormente,
∫sen(x)dx + ∫2dx
⇒-cos(x) + 2x + C
Pregunta 2: Encuentra la integral para la función dada f(x),
f(x) = 5ex
Solución:
Dado f(x) = 5e x
e x es una función estándar y se conoce su antiderivada.
∫f(x)dx
⇒∫5e x dx
Usando la propiedad 1 mencionada anteriormente,
5∫e x dx
⇒5e x + C
Pregunta 3: Encuentra la integral para la función dada f(x),
f(x) = x-1
Solución:
Dado f(x) = x-1
Usando la regla de la potencia inversa
∫f(x)dx
⇒∫(x – 1)dx
Usando la propiedad 1 mencionada anteriormente,
∫xdx – ∫1dx
⇒
Pregunta 4: Encuentra la integral para la función dada f(x),
f(x) = sen(x) + cos(x)
Solución:
Dado f(x) = sin(x) + cos(x)
sin(x) y cos(x) son funciones estándar y se conoce su integral.
\int f(x)dx
⇒∫(sen(x) + cos(x))dx
Usando las propiedades 1 y 2 mencionadas anteriormente,
∫sen(x)dx + ∫cos(x)dx
⇒-cos(x) + sen(x) + C
Pregunta 5: Dado f'(x) = e x y f(2) = 5 + e 2 encuentre el valor de f(4).
Solución:
f(x) = ∫f'(x) = ∫e x = e x + C
Se da que,
f(2) = mi 2 + C
⇒ 5 + mi 2 = mi 2 + C
⇒ C = 5
f(x) = e x +5
⇒f(4) = mi 4 +5
Pregunta 6: Dado f'(x) = 6x 2 yf(2) = 12. El objetivo es encontrar f(-1).
Solución:
Reescribamos las funciones dadas,
f(x) = ∫f'(x) = ∫6x 2 = 2x 3 + C
Se da que,
f(2) = 12
⇒ 2(2) 3 + C = 12
⇒C = -4
Introduciendo el valor de C en la ecuación de f(x),
f(x) = 2x 3 -4
f(-1) = 2(-1) 3 -4
f(-1) = -6
Pregunta 7: Dado f'(x) = 6x 2 + 4x y f(2) = 12, el objetivo es encontrar f(-1).
Solución:
Reescribamos las funciones dadas,
f(x) = ∫f'(x) = ∫6x 2 + 4x = 2x 3 + 2x 2 + C
Se da que,
f(2) = 12
⇒22 3 + 22 2 + C = 12
⇒C = -12
Introduciendo el valor de C en la ecuación de f(x),
f(x) = 2x 3 + 2x 2 -12
f(-1) = 2(-1) 3 + 2(-1) 2 – 12
f(-1) = -12
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA