Suma de los números hasta N que son divisibles por 2 o 5

Dado un número n. La tarea es encontrar la suma de números hasta n, que son divisibles por 2 o 5.
Ejemplos: 

Input: n = 2
Output: 2

Input: n = 5
Output: 11

Un enfoque ingenuo es simplemente iterar sobre los números hasta n y verificar si es divisible por 2 o 5. Si es divisible, simplemente agregue este número a nuestra suma requerida. Y finalmente, obtuvimos nuestra suma total con una complejidad de O(n).
Enfoque eficiente: 

 1. Primero encuentre los números que son divisibles por 2. Entonces, estos números para un AP, teniendo 

primer término = 2, diferencia = 2, número de términos = n/2 
Entonces, suma dada por-

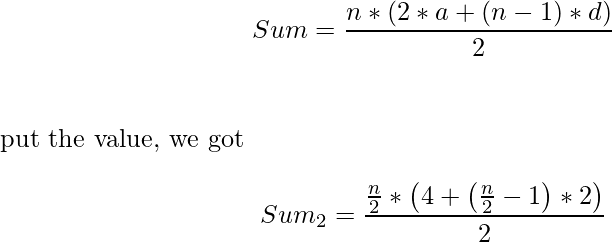
2. En segundo lugar, encontramos los números que son divisibles por 5. Entonces, estos números para un AP, teniendo 
 

primer término = 5, diferencia = 5, número de términos = n/5 
Entonces, suma dada por-

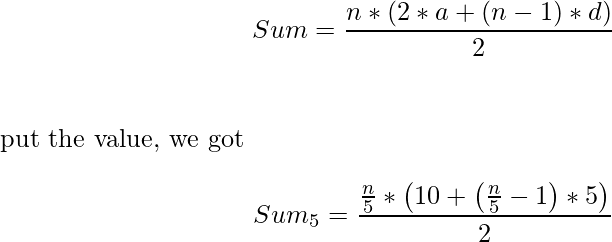
3. Primero encontramos los números que son divisibles por 2 y 5. Entonces, estos números para un AP, teniendo 
 

primer término = 10, diferencia = 10, Número de términos = n / 10 
Entonces, suma dada por-

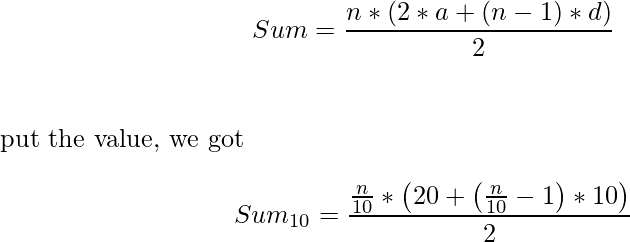
4. Como tenemos que encontrar la suma de números divisibles por 2 o 5. Entonces, la suma requerida está dada por:
 

suma = suma_2 + suma_5 – suma_10
 

A continuación se muestra la implementación del enfoque anterior: 

// C++ implementation of above approach
#include <bits/stdc++.h>
#define ll long long int
using namespace std;
 
// Function to find the sum
ll findSum(int n)
{
 
    ll sum2, sum5, sum10;
 
    // sum2 is sum of numbers divisible by 2
    sum2 = ((n / 2) * (4 + (n / 2 - 1) * 2)) / 2;
 
    // sum5 is sum of number divisible by 5
    sum5 = ((n / 5) * (10 + (n / 5 - 1) * 5)) / 2;
 
    // sum10 of numbers divisible by 2 and 5
    sum10 = ((n / 10) * (20 + (n / 10 - 1) * 10)) / 2;
 
    return sum2 + sum5 - sum10;
}
 
// Driver code
int main()
{
    int n = 5;
 
    cout << findSum(n) << endl;
    return 0;
}

// Java implementation of
// above approach
import java.lang.*;
import java.util.*;
 
class GFG
{
 
// Function to find the sum
static long findSum(int n)
{
    long sum2, sum5, sum10;
     
    // sum2 is sum of numbers
    // divisible by 2
    sum2 = ((n / 2) * (4 +
            (n / 2 - 1) * 2)) / 2;
     
    // sum5 is sum of number
    // divisible by 5
    sum5 = ((n / 5) * (10 +
            (n / 5 - 1) * 5)) / 2;
     
    // sum10 of numbers divisible
    // by 2 and 5
    sum10 = ((n / 10) * (20 +
             (n / 10 - 1) * 10)) / 2;
     
    return sum2 + sum5 - sum10;
}
 
// Driver code
public static void main (String[] args)
{
    int n = 5;
    System.out.println(findSum(n));
}
}
 
// This code is contributed by Raj

# Python3 implementation of
# above approach
 
# Function to find the sum
def findSum(n):
 
     
    # sum2 is sum of numbers divisible by 2
    sum2 = ((n // 2) * (4 + (n // 2 - 1) * 2)) // 2
 
    # sum5 is sum of number divisible by 5
    sum5 = ((n // 5) * (10 + (n // 5 - 1) * 5)) // 2
 
    # sum10 of numbers divisible by 2 and 5
    sum10 = ((n // 10) * (20 + (n // 10 - 1) * 10)) // 2
 
    return sum2 + sum5 - sum10;
 
 
# Driver code
if __name__=='__main__':
    n = 5
    print (int(findSum(n)))
     
 
# this code is contributed by Shivi_Aggarwal

// C# implementation of
// above approach
using System;
 
class GFG
{
 
// Function to find the sum
static long findSum(int n)
{
    long sum2, sum5, sum10;
     
    // sum2 is sum of numbers
    // divisible by 2
    sum2 = ((n / 2) * (4 +
            (n / 2 - 1) * 2)) / 2;
     
    // sum5 is sum of number
    // divisible by 5
    sum5 = ((n / 5) * (10 +
            (n / 5 - 1) * 5)) / 2;
     
    // sum10 of numbers divisible
    // by 2 and 5
    sum10 = ((n / 10) * (20 +
             (n / 10 - 1) * 10)) / 2;
     
    return sum2 + sum5 - sum10;
}
 
// Driver code
public static void Main ()
{
    int n = 5;
    Console.WriteLine(findSum(n));
}
}
 
// This code is contributed by inder_verma

<?php
// PHP implementation of above approach
 
// Function to find the sum
function findSum($n)
{
 
    // sum2 is sum of numbers
    // divisible by 2
    $sum2 = ((int)($n / 2) * (4 +
            ((int)($n / 2) - 1) * 2)) / 2;
     
    // sum5 is sum of number
    // divisible by 5
    $sum5 = ((int)($n / 5) * (10 +
                  ($n / 5 - 1) * 5)) / 2;
     
    // sum10 of numbers divisible
    // by 2 and 5
    $sum10 = ((int)($n / 10) * (20 +
                   ($n / 10 - 1) * 10)) / 2;
     
    return $sum2 + $sum5 - $sum10;
}
 
// Driver Code
$n = 5;
echo findSum($n);
 
// This code is contributed by Raj
?>

<script>
 
// Javascript implementation of above approach
 
// Function to find the sum
function findSum(n)
{
 
    var sum2, sum5, sum10;
 
    // sum2 is sum of numbers divisible by 2
    sum2 = parseInt((parseInt(n / 2) *
    (4 + (parseInt(n / 2) - 1) * 2)) / 2);
 
    // sum5 is sum of number divisible by 5
    sum5 = parseInt((parseInt(n / 5) *
    (10 + (parseInt(n / 5) - 1) * 5)) / 2);
 
    // sum10 of numbers divisible by 2 and 5
    sum10 = parseInt((parseInt(n / 10) *
    (20 + (parseInt(n / 10) - 1) * 10)) / 2);
 
    return sum2 + sum5 - sum10;
}
 
// Driver code
var n = 5;
document.write( findSum(n));
 
</script>

11

Tiempo Complejidad: O(1) 
Espacio Auxiliar: O(1)