Suma de todas las subsecuencias de longitud K

Dada una array arr[] y un entero K , la tarea es encontrar la suma de todas las subsecuencias de longitud K de la array dada.

Ejemplo: 

Entrada: arr[] = {2, 3, 4}, K = 2 
Salida: 18 
Explicación: 
Hay 3 subsecuencias posibles de longitud 2 que son {2, 3}, {2, 4} y {3, 4} 
La la suma de las 2 subsecuencias de longitud es 5 + 6 + 7 = 18

Entrada: arr[] = {7, 8, 9, 2}, K = 2 
Salida: 78 
Explicación: 
Hay 6 subsecuencias de longitud 2 que son {7, 8}, {7, 9}, {7, 2} , {8, 9}, {8, 2} y {9, 2}. 
La suma de las 2 subsecuencias de longitud es 15 + 16 + 9 + 17 + 10 + 11 = 78 
 

Enfoque: 
Para resolver el problema mencionado anteriormente, debemos considerar todas las subsecuencias de longitud K que son «n elige k», es decir

• El recuento del elemento total en todas las subsecuencias de longitud K es , la posibilidad de aparición de cada elemento es la misma.
• Entonces cada elemento aparece 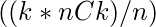veces y contribuye en el resultado.
• Por lo tanto, la suma de todas las subsecuencias de longitud K es

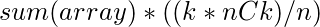
A continuación se muestra la implementación del enfoque mencionado anteriormente: 

// C++ implementation to find sum
// of all subsequences of length K
  
#include <bits/stdc++.h>
using namespace std;
  
int fact(int n);
  
// Function to find nCr
int nCr(int n, int r)
{
    return fact(n)
           / (fact(r)
              * fact(n - r));
}
  
// Function that returns
// factorial of n
int fact(int n)
{
    int res = 1;
    for (int i = 2; i <= n; i++)
        res = res * i;
    return res;
}
  
// Function for finding sum
// of all K length subsequences
int sumSubsequences(
    int arr[], int n, int k)
{
  
    int sum = 0;
  
    // Calculate the sum of array
    for (int i = 0; i < n; i++) {
        sum += arr[i];
    }
    int kLengthSubSequence;
  
    // Calculate nCk
    kLengthSubSequence = nCr(n, k);
  
    int ans
        = sum
          * ((k * kLengthSubSequence)
             / n);
  
    // Return the final result
    return ans;
}
  
// Driver code
int main()
{
  
    int arr[] = { 7, 8, 9, 2 };
  
    int K = 2;
  
    int n = sizeof(arr) / sizeof(arr[0]);
  
    cout << sumSubsequences(arr, n, K);
    return 0;
}

// Java implementation to find sum
// of all subsequences of length K
class GFG{
  
// Function to find nCr
static int nCr(int n, int r)
{
    return fact(n) / (fact(r) * fact(n - r));
}
  
// Function that returns
// factorial of n
static int fact(int n)
{
    int res = 1;
    for (int i = 2; i <= n; i++)
        res = res * i;
    return res;
}
  
// Function for finding sum
// of all K length subsequences
static int sumSubsequences(int arr[], 
                           int n, int k)
{
    int sum = 0;
  
    // Calculate the sum of array
    for (int i = 0; i < n; i++) 
    {
        sum += arr[i];
    }
    int kLengthSubSequence;
  
    // Calculate nCk
    kLengthSubSequence = nCr(n, k);
  
    int ans = sum * ((k * kLengthSubSequence) / n);
  
    // Return the final result
    return ans;
}
  
// Driver code
public static void main(String[] args)
{
    int arr[] = { 7, 8, 9, 2 };
  
    int K = 2;
  
    int n = arr.length;
  
    System.out.print(sumSubsequences(arr, n, K));
}
}
  
// This code contributed by Rajput-Ji

# Python3 implementation to find sum 
# of all subsequences of length K
  
# Function to find nCr 
def nCr(n, r):
      
    return fact(n) / (fact(r) * 
                      fact(n - r))
  
# Function that returns 
# factorial of n
def fact(n):
      
    res = 1
    for i in range(2, n + 1):
        res = res * i 
    return res
      
# Function for finding sum 
# of all K length subsequences
def sumSubsequences(arr, n, k):
      
    sum = 0
      
    # Calculate the sum of array 
    for i in range(0, n):
        sum = sum + arr[i]
      
    # Calculate nCk     
    kLengthSubSequence = nCr(n, k)
    ans = sum * ((k * kLengthSubSequence) / n);
      
    # Return the final result 
    return ans
  
# Driver Code 
arr = [ 7, 8, 9, 2 ]
k = 2
n = len(arr)
  
print(sumSubsequences(arr, n, k))
  
# This code is contributed by skylags    

// C# implementation to find sum
// of all subsequences of length K
using System;
  
class GFG{
      
// Function to find nCr
static int nCr(int n, int r)
{
    return fact(n) / (fact(r) * fact(n - r));
}
      
// Function that returns
// factorial of n
static int fact(int n)
{
    int res = 1;
      
    for(int i = 2; i <= n; i++)
       res = res * i;
    return res;
}
      
// Function for finding sum
// of all K length subsequences
static int sumSubsequences(int[] arr, 
                           int n, int k)
{
    int sum = 0;
      
    // Calculate the sum of array
    for(int i = 0; i < n; i++) 
    {
       sum += arr[i];
    }
      
    int kLengthSubSequence;
      
    // Calculate nCk
    kLengthSubSequence = nCr(n, k);
    int ans = sum * ((k * kLengthSubSequence) / n);
      
    // Return the final result
    return ans;
}
  
// Driver code
static void Main() 
{
    int[] arr = { 7, 8, 9, 2 };
    int K = 2;
    int n = arr.Length;
          
    Console.Write(sumSubsequences(arr, n, K));
}
}
  
// This code is contributed by divyeshrabadiya07

<script>
  
// Javascript implementation to find sum
// of all subsequences of length K
  
// Function to find nCr
function nCr(n, r)
{
    return fact(n) / (fact(r) * 
           fact(n - r));
}
  
// Function that returns
// factorial of n
function fact(n)
{
    var res = 1;
    for(var i = 2; i <= n; i++)
        res = res * i;
          
    return res;
}
  
// Function for finding sum
// of all K length subsequences
function sumSubsequences(arr, n, k)
{
    var sum = 0;
  
    // Calculate the sum of array
    for(var i = 0; i < n; i++)
    {
        sum += arr[i];
    }
    var kLengthSubSequence;
  
    // Calculate nCk
    kLengthSubSequence = nCr(n, k);
  
    var ans = sum * ((k * 
              kLengthSubSequence) / n);
  
    // Return the final result
    return ans;
}
  
// Driver code
var arr = [ 7, 8, 9, 2 ];
var K = 2;
var n = arr.length;
  
document.write(sumSubsequences(arr, n, K));
  
// This code is contributed by noob2000
  
</script>

78