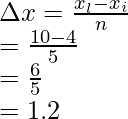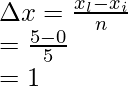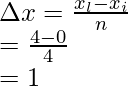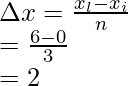Sumas de Riemann en notación de sumatoria

Las sumas de Riemann nos permiten calcular el área bajo la curva para cualquier función arbitraria. Estas formulaciones nos ayudan a definir la integral definida. La idea básica detrás de estas sumas es dividir el área que se supone que debe calcularse en pequeños rectángulos y calcular la suma de sus áreas. Estas áreas no son precisas, pero ayudan mucho a tener una idea del área real. Cuanto mayor sea el número de rectángulos, más nos acercará al área real. Veamos las sumas de Riemann con notaciones sigma.

Sumas de Riemann

Las integrales definidas son una parte importante del cálculo. Se utilizan para calcular áreas, volúmenes, etc. de formas arbitrarias para las que no se han definido fórmulas. Analíticamente son solo integrales indefinidas con límites encima de ellas, pero gráficamente representan el área bajo la curva. Los límites denotan los límites entre los cuales se debe calcular el área. Estos conceptos tienen mucha importancia en el campo de la ingeniería eléctrica, robótica, etc. Para definir integrales se utilizan sumas de Riemann en las que calculamos el área bajo cualquier curva utilizando rectángulos infinitesimalmente pequeños. Veamos esta interpretación de integrales definidas en detalle.

Ahora, esta área se puede dividir en varios rectángulos, suponiendo que el área se divida en ‘n’ rectángulos de igual ancho. Algunos de estos rectángulos van por encima del valor real de la función y otros por debajo, lo que significa que el área está sobreestimada y subestimada en ciertas partes. La altura de estos rectángulos está determinada por el valor de la función en el medio del intervalo.

En la notación integral definida, esta área se representará como,

$\int^{b}_{a}f(x)dx$

Esta área se puede aproximar dividiendo el área bajo la curva en n rectángulos de igual tamaño. Entonces, el intervalo [a, b] se divide en n-subintervalos definidos por los puntos.

a = x ₀ < x ₁ < x ₂ < …. x _n-2 < x _n-1 < x _n = segundo

Entonces, los n intervalos son,

[x ₀ , x ₁ ], [x ₁ , x ₂ ], …. [x _n-1 , x _n ]

Entonces, para el i ^-ésimo rectángulo, el ancho será [x _i-1 , x _i ].

El área del i ^-ésimo rectángulo A _i = f( $\frac{x_{i-1} + x_{i}}{2}$ )(x _{i —} x _i-1 )

Entonces, el área total será $\sum^{n}_{i = 1}A_{i}$

Esta suma se llama suma de Riemann .

Sumas de Riemann en notación Sigma

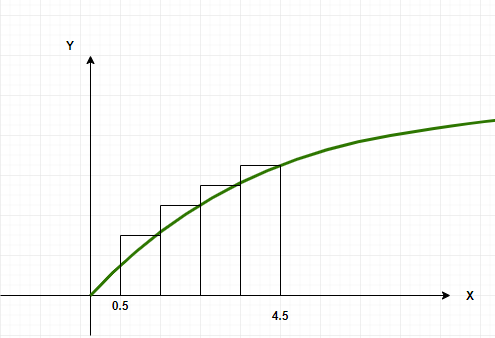
Supongamos que el objetivo es calcular el área bajo la gráfica de la función f(x) = x ² , el área se calculará entre los límites x = 0,5 a x = 4,5.

Divide el intervalo en cuatro partes iguales, los intervalos serán [0.5, 1.5], [1.5, 2.5], [2.5, 3.5] y [3.5, 4.5].

Entonces, la suma de Riemann se puede escribir de la siguiente manera,

A(1) + A(2) + A(3) + A(4) = $\sum^{4}_{i=1}A_{i}$

Sean las alturas del intervalo los valores de la función al final del rectángulo. Esto se llama la suma de la derecha Suma de Riemann . Sea x _i el extremo derecho del i ^-ésimo rectángulo.

Entonces, la fórmula para x _i = 0.5 + i. Ahora, el valor de la función en estos puntos se convierte en,

f(x _yo ) = (0.5 + yo) ²

Entonces, A(i) = (alto)(ancho)

= (0.5 + yo) ²

La suma de Riemann se convierte en,

A(1) + A(2) + A(3) + A(4) = $\sum^{4}_{i=1}A_{i}$

⇒ A(1) + A(2) + A(3) + A(4) = $\sum^{4}_{i=1}(0.5 + i)^2$

Entonces, de esta manera, casi todas las sumas de Riemann se pueden representar en una notación sigma.

Para resumir todo el proceso,

Paso 1: Averigüe el ancho de cada intervalo. Denotemos el ancho del intervalo con $\Delta x$

Paso 2: Sea x _i el extremo derecho del rectángulo x _i = a + $\Delta$ xi

Paso 3: Defina el área de cada rectángulo.

Paso 4: Suma las áreas

Problemas de muestra

Pregunta 1: Considere una función f(x), su área se calcula a partir de la suma de Riemann de x = 4 a x = 10, el área total se divide en 5 rectángulos. Encuentre el ancho del intervalo.

Solución:

La longitud total se divide en 5 partes iguales,

x _{i =} 4 y x _l = 10,

El ancho de un intervalo viene dado por = $\frac{x_{l} -x_{i}}{n}$

Donde x _i – punto inicial, y x _l – último punto y n= número de partes

norte = 5

$\Delta x = \frac{x_l - x_i}{n} \\ = \frac{10 - 4}{5} \\ = \frac{6}{5} \\ = 1.2$

Pregunta 2: Considere una función f(x) = x, su área se calcula a partir de la suma de Riemann de x = 0 a x = 5, el área total se divide en 5 rectángulos. Encuentre la suma de Riemann en notación sigma

Solución:

Paso (i): Calcular el ancho

La longitud total se divide en 5 partes iguales,

x _i = 0 y x _l = 5,

El ancho de un intervalo viene dado por = $\frac{x_{l} -x_{i}}{n}$

Donde x _i = punto inicial, y x _l – último punto y n= número de partes

norte = 5

$\Delta x = \frac{x_l - x_i}{n} \\ = \frac{5 - 0}{5} \\ = 1$

Paso (ii) :

un = 0,

x _yo = 0 + $\Delta x.i$

⇒ x _yo = yo

Paso (iii)

A _i = Alto x Ancho

= f(x _i ) $\Delta x$

= (yo)

Área total = A(1) + A(2) + A(3) + A(4) + A(5)

= $\sum^{5}_{i=1}i$

Pregunta 3: Considere una función f(x) = 5 – x, su área se calcula a partir de la suma de Riemann de x = 0 a x = 5, el área total se divide en 5 rectángulos. Encuentre la suma de Riemann en notación sigma

Solución:

Paso (i): Calcular el ancho

La longitud total se divide en 5 partes iguales,

x _i = 0 y x _l = 5,

El ancho de un intervalo viene dado por = $\frac{x_{l} -x_{i}}{n}$

Donde x _i = punto inicial, y x _l – último punto y n= número de partes

norte = 5

$\Delta x = \frac{x_l - x_i}{n} \\ = \frac{5 - 0}{5} \\ = 1$

Paso (ii):

un = 0,

x _yo = 0 + $\Delta x.i$

⇒ x _yo = yo

Paso (iii)

A _i = Alto x Ancho

= f(x _i ) $\Delta x$

= (5 – i)(1)

= 5 – yo

Área total = A(1) + A(2) + A(3) + A(4) + A(5)

= $\sum^{5}_{i=1}5 - i$

Pregunta 4: Considere una función f(x) = √x, su área se calcula a partir de la suma de Riemann de x = 0 a x = 4, el área total se divide en 4 rectángulos. Encuentre la suma de Riemann en notación sigma

Solución:

Paso (i): Calcular el ancho

La longitud total se divide en 4 partes iguales,

x _i = 0 y x _l = 4,

El ancho de un intervalo viene dado por = $\frac{x_{l} -x_{i}}{n}$

Donde x _i = punto inicial, y x _l – último punto y n= número de partes

norte = 4

$\Delta x = \frac{x_l - x_i}{n} \\ = \frac{4 - 0}{4} \\ = 1$

Paso (ii):

un = 0,

x _yo = 0 + $\Delta x.i$

⇒ x _yo = yo

Paso (iii)

Ai = _Alto × Ancho

= f(x _i ) $\Delta x$

= (√i)(1)

= √i

Área total = A(1) + A(2) + A(3) + A(4)

= $\sum^{4}_{i=1}\sqrt{i}$

Pregunta 5: Considere una función f(x) = e ^x + 1, su área se calcula a partir de la suma de Riemann de x = 0 a x = 4, el área total se divide en 4 rectángulos. Encuentre la suma de Riemann en notación sigma

Solución:

Paso (i): Calcular el ancho

La longitud total se divide en 4 partes iguales,

x _i = 0 y x _l = 4,

El ancho de un intervalo viene dado por = $\frac{x_{l} -x_{i}}{n}$

Donde x _i = punto inicial, y x _l – último punto y n= número de partes

norte = 4

$\Delta x = \frac{x_l - x_i}{n} \\ = \frac{4 - 0}{4} \\ = 1$

Paso (ii):

un = 0,

x _yo = 0 + $\Delta x.i$

⇒ x _yo = yo

Paso (iii)

A _i = Alto x Ancho

= f(x _i ) $\Delta x$

= (e ⁱ + 1)(1)

= mi ^yo + 1

Área total = A(1) + A(2) + A(3) + A(4)

= $\sum^{4}_{i=1}(e^i + 1)$

Pregunta 6: Considere una función f(x) = x ² + x, su área se calcula a partir de la suma de Riemann de x = 0 a x = 6, el área total se divide en 3 rectángulos. Encuentre la suma de Riemann en notación sigma

Solución:

Paso (i): Calcular el ancho

La longitud total se divide en 4 partes iguales,

x _i = 0 y x _l = 6,

El ancho de un intervalo viene dado por = $\frac{x_{l} -x_{i}}{n}$

Donde x _i = punto inicial, y x _l – último punto y n= número de partes

norte = 3

$\Delta x = \frac{x_l - x_i}{n} \\ = \frac{6 - 0}{3} \\ = 2$

Paso (ii):

un = 0,

x _yo = 0 + $\Delta x.i$

⇒ x _yo = 2i

Paso (iii)

A _i = Alto x Ancho

= f(x _i ) $\Delta x$

= (yo ² + yo)(2)

Área total = A(1) + A(2) + A(3) + A(4) + A(5) + A(6)

= $\sum^{4}_{i=1}(i^2 + i)$

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Sumas de Riemann

Sumas de Riemann en notación Sigma

Problemas de muestra

Deja una respuesta Cancelar la respuesta