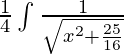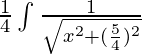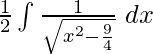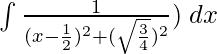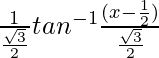La integración por sustitución es un enfoque bueno y más fácil que cualquiera puede hacer. Se usa cuando hacemos una sustitución de una función, cuya derivada ya está incluida en la función integral dada. Con esto, la función se simplifica y se obtiene una función integral simple que podemos integrar fácilmente. También se conoce como sustitución de u o la regla de la string inversa. O en otras palabras, usando este método, podemos evaluar fácilmente integrales y antiderivadas.
El método de integración por sustitución:
Tomemos una integral I = ∫f(x)dx …..(i)
Ahora podemos transformar esta integral cambiando su variable independiente x por u sustituyendo x = g(u).
Derivamos g(u) wrtx, obtenemos
dx/du = g'(u)
o podemos escribir como
dx = g'(u) du
Ahora ponga todos estos valores en la ecuación (i), obtenemos
∫f(x)dx = ∫f(g(u)).g'(u) du
Por lo tanto, la forma general de integración por sustitución es
∫f(g(x)).g′(x).dx = ∫f(u).dt
Aquí u = g(x). Las integraciones por sustitución son de dos tipos:
1. Sustitución directa: La sustitución directa sigue el teorema de integración por sustitución.
Teorema:
Supongamos que f es la función definida en el intervalo I y tiene una función inversa F. Sea g la función del intervalo H en el intervalo I que es derivable en H. Entonces, F(g) es una función inversa o antiderivada de f( g)g’ en H:
∫f(g(x)).g′(x).dx = ∫f(y).dy\ y = g(x)
En sustitución directa, si la integral dada tiene la forma de ∫f(g(x)).g′(x).dx(reordenando). Entonces podemos transformar esta integral cambiando su variable independiente x a u sustituyendo u = g(x).
∫f(g(x)).g′(x).dx = ∫f(u).g′(x).dx
Ahora tenemos que reemplazar g′(x)dx con du.
Entonces obtenemos
∫f(g(x)).g′(x).dx = ∫f(u).du
Ahora el resultado final es de esta forma.
F(u) + C = F(g(x)) + C
Ejemplo:
Como, aquí es 8x no 2x.
Luego intentaremos que encaje en la definición. Creamos su derivada aquí y hacemos algunas reorganizaciones de funciones.
=
= 4
= 4 (- cos(u) + c)
= – 4 cos(u) + c 1 (c 1 = 4c)
Ahora, reemplazando u = x 2, obtenemos
= – 4 cos(x 2 ) + c 1
2. Sustitución Indirecta: También es un método que incluye la sustitución por simplificación, pero invierte la sustitución directa.
En sustitución indirecta, si la integral dada tiene la forma de ∫f(u).du. Entonces podemos transformar esta integral de vuelta a su variable independiente original u en x sustituyendo u = g(x).
∫f(u).du =
Ahora tenemos que reemplazar du con g′(x)dx.
Entonces obtenemos
= g′(x)dx
Ahora el resultado final es de esta forma.
G(u) + C = G(g -1 (x)) + C
Como se mencionó anteriormente, parece que seguimos la sustitución directa anterior en la dirección opuesta. La sustitución indirecta se usa muy raramente, pero hay tipos específicos de integrales. En general, es útil donde tienen lugar integrales con raíces.
Ejemplo:
vamos a sustituir
tu =
tu 2 = x 3 + 5
Derivando, frente a x, obtenemos
2u du/dx = 3x 2
x 2 dx = 2/3u du
Sustituyendo estos valores, obtenemos
2/9 tu 3 + do 1 (do 1 = 2/9 do)
Como, u =
, obtenemos
yo =
+ c 1
Sustitución trigonométrica
La sustitución trigonométrica es un proceso en el que tiene lugar la sustitución de una función rigurosonmétrica por otra expresión. Se utiliza para evaluar integrales o es un método para encontrar antiderivadas de funciones que contienen raíces cuadradas de expresiones cuadráticas o potencias racionales de la forma ![]() (donde p es un número entero) de expresiones cuadráticas. Ejemplos de tales expresiones son
(donde p es un número entero) de expresiones cuadráticas. Ejemplos de tales expresiones son
![]() or
or ![]() or etc……
or etc……
Se puede recurrir al método de sustitución trigonométrica cuando han fallado otros métodos de integración más comunes y fáciles de usar. La sustitución trigonométrica supone que está familiarizado con las identidades trigonométricas estándar, el uso de la notación diferencial, la integración mediante la sustitución u y la integración de funciones trigonométricas.
x = f()
dx = f'()d
Aquí, discutiremos algunas fórmulas importantes dependiendo de la función que necesitemos integrar, sustituimos una de las siguientes expresiones trigonométricas para simplificar la integración:
Las siguientes son algunas sustituciones útiles para evaluar integrales:
| Expresión | Sustitución |
|---|---|
| un 2 + x 2 |
x = a tan θ o x = una cuna θ |
| un 2 – x 2 |
x = a sen θ o x = a cos θ |
| x 2 – un 2 |
x = un segundo θ o x = a cosec θ |
| x = a cos 2θ | |
| x = ∝ cos 2 θ + β sen 2 θ |
Integrandos que consisten en 2 – x 2 .
Ejemplo:
Pongamos, x = a senθ
dx = a cosθ dθ
yo =
yo =
yo =
yo = θ + c
Como, x = a senθ
⇒ θ =
yo =
Integrandos que consisten en x 2 + a 2 .
Ejemplo:
Pongamos x = a tanθ
dx = a sec2θ dθ, obtenemos
yo =
yo =
yo =
yo =
+ c
Como, x = a tanθ
⇒ θ =
yo =
+ c
Integrandos que consisten en 2 + x 2 .
Ejemplo:
Pongamos, x = a tanθ
dx = un segundo 2 θ dθ
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Integrandos que consisten en x 2 – a 2 .
Ejemplo:
Pongamos, x = a secθ
dx = a secθ tanθ dθ
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Problemas de muestra
Pregunta 1. ![]()
Solución:
Tomando 5 común en denominador,
yo =
yo =
Según el teorema 1, a =
yo =
+ c
yo =
+ c
Pregunta 2. ![]()
Solución:
Tomando √2 común en el denominador,
yo =
yo =
Según el teorema 1, a = 2
yo =
+c
yo =
+c
Pregunta 3. ![]()
Solución:
Reordenando, obtenemos
Aquí tomando,
un = 3
x = 3 senθ
dx = 3 cos θ dθ
Sustituyendo estos valores,
yo =
yo =
yo =
yo = 243
yo = 243
Echemos,
tu = cos θ
du = -sen θ dθ
Sustituyendo estos valores, obtenemos
yo = 243
yo = -243
yo = -243
yo = -243
Como, u = cos θ y x = 3 senθ
cos θ =
tu =
tu =
Por eso,
yo = -243
yo = -243
+ c
Pregunta 4. ![]()
Solución:
Tomando 9 común en denominador,
yo =
yo =
Según el teorema 2, a =
yo =
yo =
Pregunta 5. ![]()
Solución:
Tomando 4 común en denominador,
yo =
yo =
Según el teorema 3, a =
yo =
yo =
yo =
yo =
Pregunta 6. ![]()
Solución:
Tomando 2 común en denominador,
yo =
yo =
Según el teorema 4, a =
yo =
yo =
yo =
yo =
yo =
Pregunta 7. ![]()
Solución:
Después de reorganizar, obtenemos
yo =
yo =
yo =
yo =
De acuerdo con el teorema 2, tenemos
x = x-
y a =
yo =
yo =
Publicación traducida automáticamente
Artículo escrito por _shinchancode y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
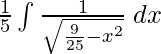
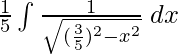
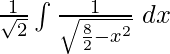
![Rendered by QuickLaTeX.com [\frac{({(1-\frac{x^2}{9})^{\frac{1}{2}})}^3}{3}-\frac{({(1-\frac{x^2}{9})^{\frac{1}{2}})}^5}{5}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f610602ccf7d5de6a8e67fe7709d80d3_l3.png)