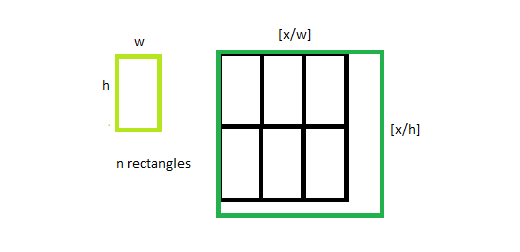
Tamaño del cuadrado más pequeño que contiene N rectángulos no superpuestos de dimensiones dadas

Posted on by Rudeus Greyrat

Dados dos enteros positivos W y H y N rectángulos de dimensión W*H , la tarea es encontrar el tamaño más pequeño del cuadrado requerido para que todos los N rectángulos puedan empaquetarse sin superponerse. 

Ejemplos:

Entrada: N = 10, W = 2, H = 3
Salida: 9
Explicación:
El tamaño más pequeño del cuadrado es de 9 unidades para empaquetar los 10 rectángulos dados de tamaño 2*3 como se ilustra en la siguiente imagen:

Entrada: N = 1, W = 3, H = 3
Salida: 3

Enfoque: El problema dado se basa en las siguientes observaciones:

  • Se puede demostrar que uno de los espaciamientos óptimos de los rectángulos dentro de un cuadrado viene dado por:

  • El número máximo de rectángulos de dimensión W*H, que se pueden encajar en el cuadrado de lados X viene dado por ⌊X/W⌋⋅⌊X/H⌋ .
  • La función anterior es monótonamente creciente. Por lo tanto, la idea es usar la búsqueda binaria para encontrar el lado más pequeño de un cuadrado que satisfaga la condición dada.

Siga los pasos a continuación para resolver el problema:

  • Inicialice dos variables, digamos bajo como 1 y alto como W*H*N .
  • Iterar hasta que i sea menor que j y realizar los siguientes pasos:
    • Encuentre el valor de mid como (i + j)/2 .
    • Ahora, si el valor (mid/W)*(mid/H) es como máximo N , actualice el valor de high como mid .
    • De lo contrario, actualice el valor de low como (mid + 1) .
  • Después de completar los pasos anteriores, imprima el valor de alto como el valor resultante.

A continuación se muestra la implementación del enfoque anterior:

C++

// CPP program for the above approach
#include<bits/stdc++.h>
using namespace std;
 
// Function to check if side of square X
// can pack all the N rectangles or not
bool bound(int w, int h, int N, int x)
{
     
    // Find the number of rectangle
    // it can pack
    int val = (x / w) * (x / h);
 
    // If val is atleast N,
    // then return true
    if (val >= N)
        return true;
 
    // Otherwise, return false
    else
        return false;
}
 
// Function to find the size of the
// smallest square that can contain
// N rectangles of dimensions W * H
int FindSquare(int N, int W, int H)
{
     
    // Stores the lower bound
    int i = 1;
 
    // Stores the upper bound
    int j = W * H * N;
 
    // Iterate until i is less than j
    while (i < j)
    {
         
        // Calculate the mid value
        int mid = i + (j - i) / 2;
 
        // If the current size of square
        // cam contain N rectangles
        if (bound(W, H, N, mid))
            j = mid;
 
        // Otherwise, update i
        else
            i = mid + 1;
    }
 
    // Return the minimum size of the
    // square required
    return j;
}
 
// Driver code
int main()
{
    int W = 2;
    int H = 3;
    int N = 10;
 
    // Function Call
    cout << FindSquare(N, W, H);
}
 
// This code is contributed by ipg2016107.

Java

// Java program for the above approach
class GFG{
     
// Function to check if side of square X
// can pack all the N rectangles or not
static boolean bound(int w, int h, int N, int x)
{
     
    // Find the number of rectangle
    // it can pack
    int val = (x / w) * (x / h);
 
    // If val is atleast N,
    // then return true
    if (val >= N)
        return true;
 
    // Otherwise, return false
    else
        return false;
}
 
// Function to find the size of the
// smallest square that can contain
// N rectangles of dimensions W * H
static int FindSquare(int N, int W, int H)
{
     
    // Stores the lower bound
    int i = 1;
 
    // Stores the upper bound
    int j = W * H * N;
 
    // Iterate until i is less than j
    while (i < j)
    {
         
        // Calculate the mid value
        int mid = i + (j - i) / 2;
 
        // If the current size of square
        // cam contain N rectangles
        if (bound(W, H, N, mid))
            j = mid;
 
        // Otherwise, update i
        else
            i = mid + 1;
    }
 
    // Return the minimum size of the
    // square required
    return j;
}
 
// Driver code
public static void main(String[] args)
{
    int W = 2;
    int H = 3;
    int N = 10;
 
    // Function Call
    System.out.print(FindSquare(N, W, H));
}
}
 
// This code is contributed by sk944795

Python3

# Python program for the above approach
 
# Function to check if side of square X
# can pack all the N rectangles or not
def bound(w, h, N, x):
 
    # Find the number of rectangle
    # it can pack
    val = (x//w)*(x//h)
     
    # If val is atleast N,
    # then return true
    if(val >= N):
        return True
       
    # Otherwise, return false
    else:
        return False
 
# Function to find the size of the
# smallest square that can contain
# N rectangles of dimensions W * H
def FindSquare(N, W, H):
 
    # Stores the lower bound
    i = 1
     
    # Stores the upper bound
    j = W * H*N
     
    # Iterate until i is less than j
    while(i < j):
       
        # Calculate the mid value
        mid = i + (j - i)//2
 
        # If the current size of square
        # cam contain N rectangles
        if(bound(W, H, N, mid)):
            j = mid
         
        # Otherwise, update i
        else:
            i = mid + 1
 
    # Return the minimum size of the
    # square required
    return j
 
# Driver Code
 
W = 2
H = 3
N = 10
 
# Function Call
print(FindSquare(N, W, H))

C#

// C# program for the above approach
using System;
 
class GFG{
 
// Function to check if side of square X
// can pack all the N rectangles or not
static bool bound(int w, int h, int N, int x)
{
     
    // Find the number of rectangle
    // it can pack
    int val = (x / w) * (x / h);
 
    // If val is atleast N,
    // then return true
    if (val >= N)
        return true;
 
    // Otherwise, return false
    else
        return false;
}
 
// Function to find the size of the
// smallest square that can contain
// N rectangles of dimensions W * H
static int FindSquare(int N, int W, int H)
{
 
    // Stores the lower bound
    int i = 1;
 
    // Stores the upper bound
    int j = W * H * N;
 
    // Iterate until i is less than j
    while (i < j)
    {
         
        // Calculate the mid value
        int mid = i + (j - i) / 2;
 
        // If the current size of square
        // cam contain N rectangles
        if (bound(W, H, N, mid))
            j = mid;
 
        // Otherwise, update i
        else
            i = mid + 1;
    }
     
    // Return the minimum size of the
    // square required
    return j;
}
 
// Driver Code
public static void Main()
{
    int W = 2;
    int H = 3;
    int N = 10;
 
    // Function Call
    Console.WriteLine(FindSquare(N, W, H));
}
}
 
// This code is contributed by ukasp

Javascript

<script>
 
// Javascript program for the above approach
 
// Function to check if side of square X
// can pack all the N rectangles or not
function bound(w, h, N, x)
{
     
    // Find the number of rectangle
    // it can pack
    let val = parseInt(x / w) * parseInt(x / h);
 
    // If val is atleast N,
    // then return true
    if (val >= N)
        return true;
 
    // Otherwise, return false
    else
        return false;
}
 
// Function to find the size of the
// smallest square that can contain
// N rectangles of dimensions W * H
function FindSquare(N, W, H)
{
     
    // Stores the lower bound
    let i = 1;
 
    // Stores the upper bound
    let j = W * H * N;
 
    // Iterate until i is less than j
    while (i < j)
    {
         
        // Calculate the mid value
        let mid = i + parseInt((j - i) / 2);
 
        // If the current size of square
        // cam contain N rectangles
        if (bound(W, H, N, mid))
            j = mid;
 
        // Otherwise, update i
        else
            i = mid + 1;
    }
 
    // Return the minimum size of the
    // square required
    return j;
}
 
// Driver code
    let W = 2;
    let H = 3;
    let N = 10;
 
    // Function Call
    document.write(FindSquare(N, W, H));
     
</script>
Producción: 

9

 

Complejidad de tiempo: O(log(W*H))
Espacio auxiliar: O(1)

Publicación traducida automáticamente

Artículo escrito por maheswaripiyush9 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *