Tasa de cambio promedio e instantánea

Posted on by Rudeus Greyrat

La tasa de cambio promedio representa el cambio total en una variable en relación con el cambio total de otra variable. La tasa de cambio instantánea, o derivada, mide la tasa de cambio específica de una variable en relación con un cambio infinitesimalmente pequeño en la otra variable. La tasa de cambio promedio de una función se puede determinar con líneas secantes y la tasa de cambio instantánea se puede determinar con líneas tangentes. Como aprenderá, estas tasas también se pueden determinar usando un tipo especial de matemáticas llamado cálculo. 

¿Cuál es la tasa de cambio? 

La tasa de cambio es el cambio en una variable en relación con el cambio en otra variable. Una tasa de cambio común es la velocidad, que mide el cambio en la distancia recorrida en relación con el tiempo transcurrido. El medallista de oro olímpico, Usain Bolt, se convirtió en el hombre más rápido del mundo corriendo a una velocidad máxima de 44,72 km/h durante los 100 metros lisos. En promedio, su velocidad fue un poco más lenta (no obstante, muy impresionante) a 37,58 km/h. La velocidad máxima de Bolt es un ejemplo de una tasa de cambio instantánea, y su velocidad promedio es una tasa de cambio promedio. 

Tasa de cambio promedio 

Las rectas secantes se encuentran conectando dos puntos en una curva. La pendiente de la línea secante entre dos puntos representa la tasa de cambio promedio en ese intervalo. 

Fórmula:

Tasa de cambio promedio = Pendiente (m) = △y/△x =  \frac{y_{2} - y_{1}}{x_{2} - x_{1}}  = \frac{f(x_{1}) - f(x_{0})}{x_{1} - x_{0}}

Cómo encontrar la tasa de cambio promedio entre dos puntos usando una línea secante:

Paso 1: Dibuja una línea secante que conecte los dos puntos. 

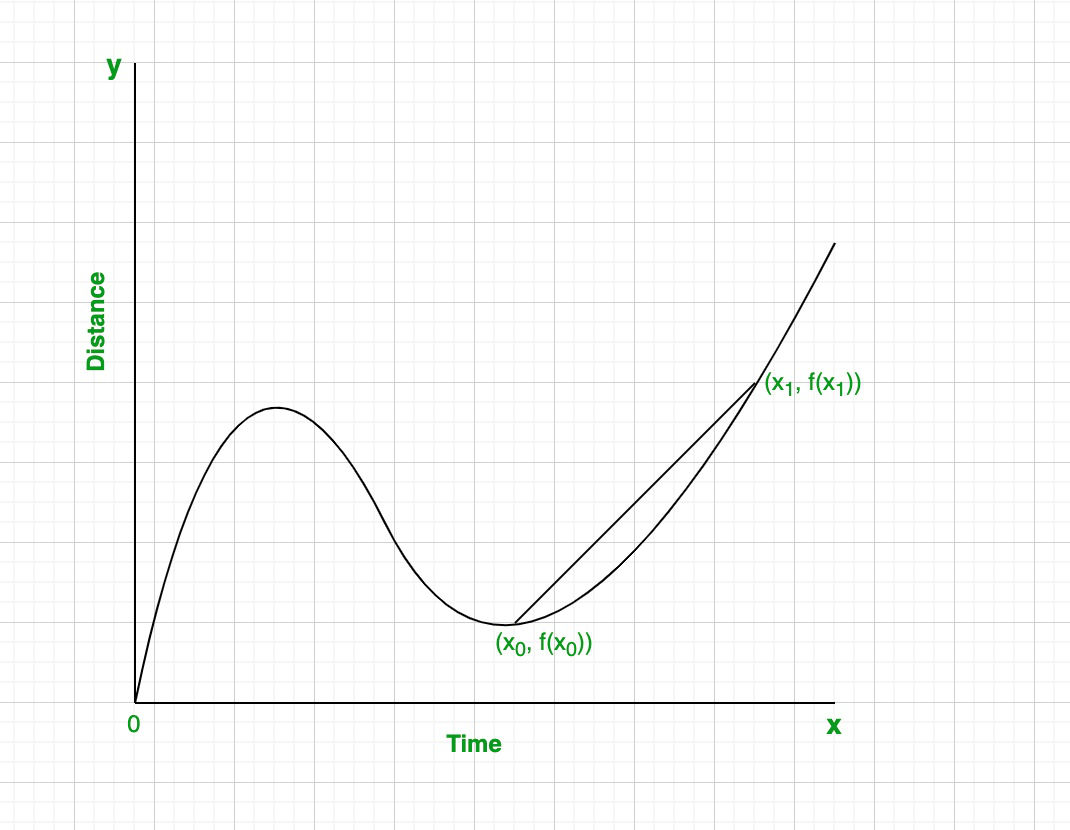
Paso 2: Usa las coordenadas de los dos puntos para calcular la pendiente. 

Ecuación de pendiente: 
Pendiente =\frac{y_{2} - y_{1}}{x_{2} - x_{1}}

El cambio promedio de la función durante el intervalo de tiempo dado [x 0 , x 1 ] 
Pendiente = \frac{f(x_{1}) - f(x_{0})}{x_{1} - x_{0}}

La pendiente de la línea secante representa la 
tasa de cambio promedio de la gráfica en ese intervalo. 

Una vez que hayas calculado la pendiente de la línea secante, puedes usar la pendiente para escribir una ecuación que la represente. 

Por ejemplo: 
Ecuación de la pendiente: 
y – y 0 = m(x – x 0 ) 

m = pendiente de la recta secante = 4/7 
x 0 = 2 
y 0 = 9 
y - 9 = \frac{4}{7}(x -2)

Por tanto, la ecuación de la recta secante entre x = 2 y x = 9 es  
y – 9 = \frac{4}{7}(x-2)

Derivados (tasa de cambio instantánea)

La línea tangente en un punto se encuentra dibujando una línea recta que toca una curva en ese punto sin cruzar la curva. En otras palabras, la línea debe tocar localmente solo un punto. La pendiente de la recta tangente en un punto representa la tasa de cambio instantánea, o derivada, en ese punto. 

Fórmula:

Tasa instantánea de cambio = f'(x_0) = \lim_{(x_0 \to x_1)} \frac{f(x_{1}) - f(x_{0})}{x_{1} - x_{0}}=\lim_{\triangle x \to 0} \frac{f(x_{0}-\triangle x) - f(x_{0})}{\triangle x}

Cómo encontrar la derivada en un punto usando una recta tangente:

Paso 1: Dibuja una línea tangente en el punto. 

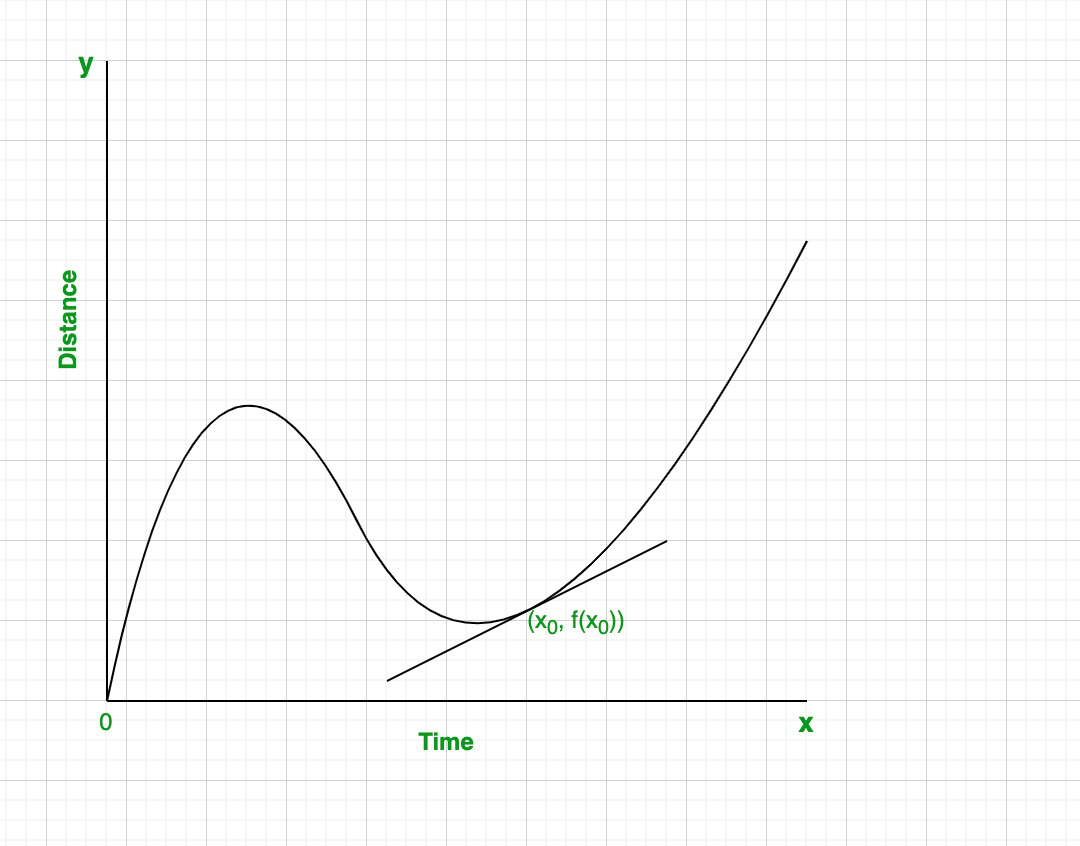
Paso 2: usa las coordenadas de dos puntos cualquiera en esa línea para calcular la pendiente. 

Ecuación de pendiente: 
Pendiente = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}

El cambio promedio de la función durante el intervalo de tiempo dado x 0 
Pendiente = f'(x_0) = \lim_{(x_0 \to x_1)} \frac{f(x_{1}) - f(x_{0})}{x_{1} - x_{0}}=\lim_{\triangle x \to 0} \frac{f(x_{0}-\triangle x) - f(x_{0})}{\triangle x}

La pendiente de la recta tangente en un punto representa 
la tasa de cambio instantánea, o derivada, en ese punto.

Una vez que hayas calculado la pendiente de la recta tangente, puedes escribir una ecuación para representarla.

Por ejemplo: Ecuación de la pendiente: 
y – y 0 = m(x – x 0 ) 

m = pendiente de la recta tangente =  \frac{5}{6}
x 0 = 16 
y 0 = 6 
y - 16 = \frac{5}{6}(x - 6)

Por lo tanto, la ecuación de la recta tangente en x = 16 es  
y – 16 = \frac{5}{6}(x – 6)  

Notación Derivada

A principios del siglo XVIII, hubo controversia entre los grandes matemáticos Isaac Newton y Gottfried Wilhelm Leibniz sobre quién fue el primero en inventar el cálculo. Este argumento se conoció como Prioritätsstreit , o “disputa de prioridad” en alemán. El desacuerdo ha tenido un impacto duradero en el mundo matemático, dejándonos con dos notaciones derivadas estándar. La notación de Lagrange es otra notación derivada común, establecida por el matemático y filósofo francés Joseph-Louis Lagrange . 

Si tomamos la función y = f(x), Entonces

1. Notación de Leibniz:

“Primera derivada de y con respecto a x” 
⇒\frac{dy}{dx}

“Segunda derivada de y con respecto a x” 
⇒\frac{dy^2}{d^2x}

“Primera derivada de y con respecto a x 
en x = 2″ 
⇒\frac{dy}{dx}|_{x=2}

2. Notación de Newton: 

El número de puntos sobre la 
variable de la función representa cuántas veces 
se ha derivado la función. 
“Primera derivada de y” 
⇒ \dot y
“Segunda derivada de y” 
⇒ \ddot y
“Primera derivada de y en x = 2” 
⇒\dot y (2)

3. Notación de Lagrange: 

El número de apóstrofes después de la 
variable de función representa cuántas veces 
se ha diferenciado la función. 
“Primera derivada de y” 
⇒y’ 
“Primera derivada de y en x = 2” 
⇒y'(2) 
“Segunda derivada de y” 
⇒y”

4. Notación de Euler

“Primera derivada” 
⇒ D x f 
“Segunda derivada” 
⇒ D x 2 f 
Aquí, D representa el operador diferencial

Problemas de muestra

Pregunta 1. Encuentra la tasa de cambio promedio en el intervalo x = 4, x = 6.

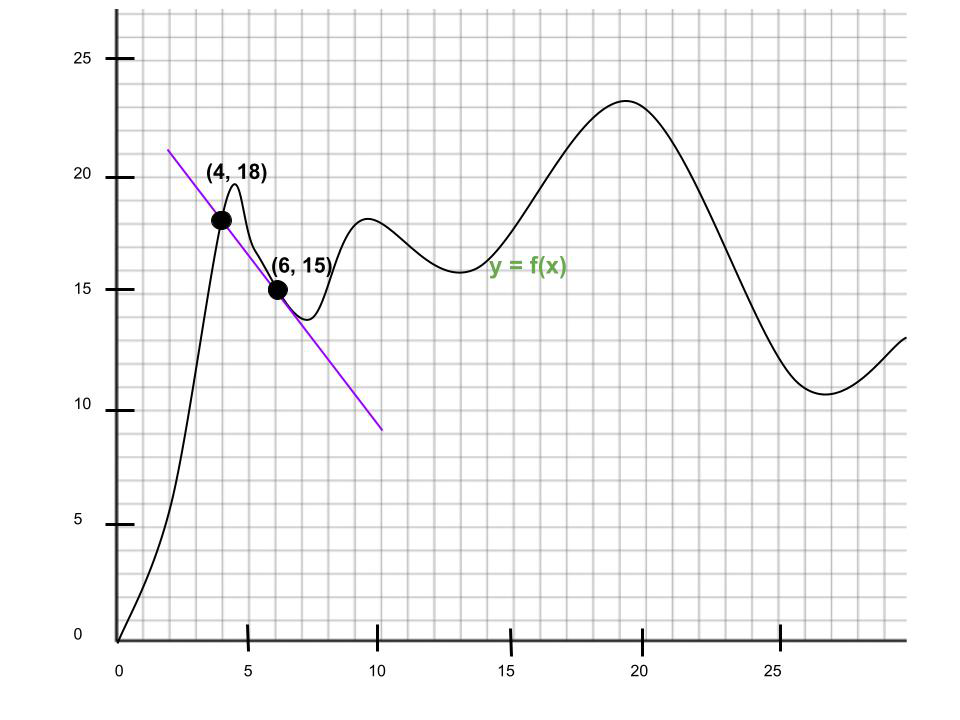
Solución:

Punto 1: (4, 18)

Punto 2: (6, 15)

Pendiente = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}

= \frac{15 - 18}{6-4}

= -\frac{3}{2}

Por lo tanto, la tasa de cambio promedio = - \frac{3}{2}
 

Pregunta 2. Escribe la ecuación de la recta tangente en x = 16. 

Solución:

Punto de intersección: (16, 18)

Pendiente = \frac{23 - 18}{18 - 16}

= \frac{5}{2}

Ecuación de la recta tangente: 

 y - 18 = \frac {5}{2}(x - 16)  

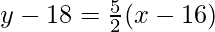
Pregunta 3. ¿Cuál es la derivada de la gráfica en x = 20? Exprese su respuesta en notación de Leibniz. 

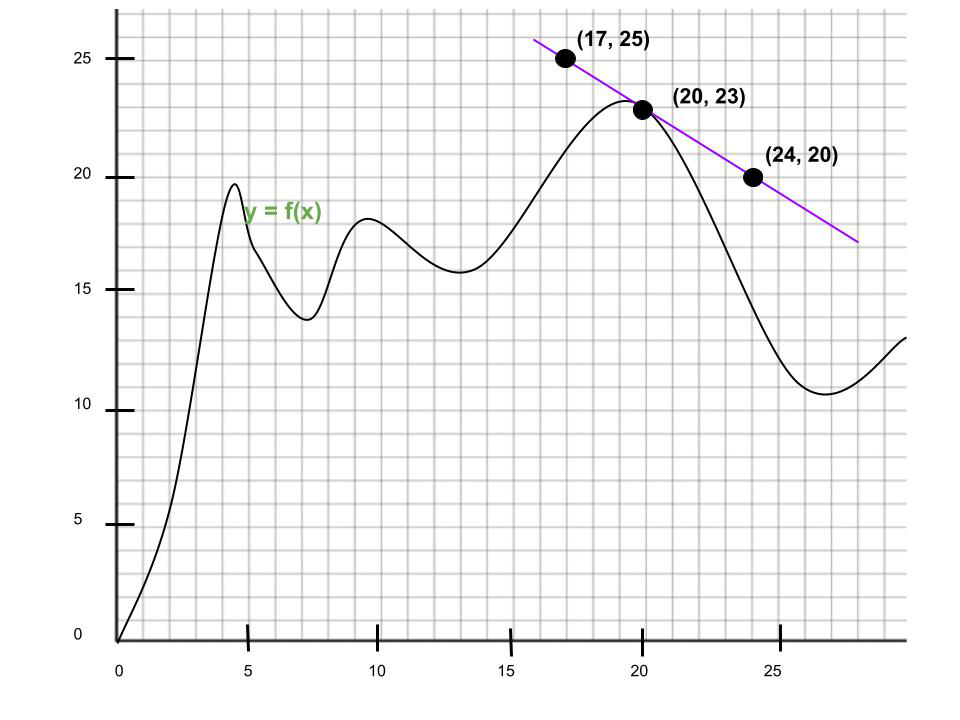
Solución:

Punto de intersección dado: (20, 23)

Pendiente de la recta tangente = \frac{20-25}{20-17}

= -\frac{5}{3}

Entonces, la notación de Leibniz: \frac {dy}{dx} | _{x=20} = -\frac{5}{3}

Pregunta 4. Encuentra la derivada de la gráfica en x = 4. Exprese su respuesta en la notación de Newton.

Solución:

Punto de intersección dado: (4, 18) 

Pendiente de la recta tangente = \frac{25 - 18}{7-4} = \frac{7}{3}

Entonces, la notación de Newton\dot y(4) = \frac{7}{3}

Pregunta 5. Encuentra la tasa de cambio promedio en el intervalo x = 4, x = 25. ¿Cómo se compara esto con la derivada en x = 4? 

Solución:

Pendiente de la recta secante = \frac {12 - 18}{25-4}

= - \frac{6}{21}

La tasa de cambio promedio sobre x = 4, x = 25 es -6/21, 

que es menor que la derivada de y en x = 4, que encontramos que

ser 7/3. 

Pregunta 6. ¿Encuentra la tasa de cambio instantánea de la función dada f(x) = 2x 2  + 18 en x = 9?
 

Solución:

Dado: f(x) = 2x 2  + 18

f'(x) = 4x + 0

f'(x) = 4x 

Ahora tenemos que encontrar la tasa de cambio instantáneo en x = 9

f(9) = 4x

f(9) = 4(9)

f(9) = 36

Pregunta 7. ¿Encuentra la tasa de cambio instantáneo de la función dada f(x) = 4x 2  + 12x + 8 en x = 4?

Solución:

Dado: f(x) = 4x 2  + 12x + 8 

f'(x) = 8x + 12

Ahora tenemos que encontrar la tasa de cambio instantáneo en x = 4

f(4) = 8x + 12

f(4) = 8(4) + 12

f(4) = 44

Publicación traducida automáticamente

Artículo escrito por sophmliu y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *