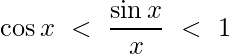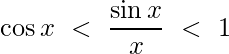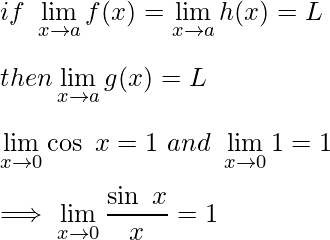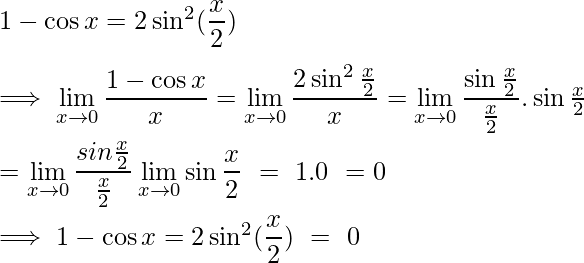Teorema de compresión – Límites

El teorema del apretón también se conoce como el teorema del sándwich , la regla del sándwich , el teorema de la policía , el teorema del pellizco, a veces el lema del apretón , el teorema de los carabinieri se usa en el análisis matemático para encontrar el límite de una función cuando hay otras dos funciones cuyos límites se sabe que están presentes. El teorema del apretón se aplica en cálculo y análisis matemático. Por lo general, se aplica para confirmar el límite de una función mediante la comparación con otras dos funciones cuyos límites se conocen o se calculan fácilmente. Primero fue utilizado geométricamente por los matemáticos Arquímedes y Eudoxo en un esfuerzo por calcular π y fue formulado en términos modernos por Carl Friedrich Gauss.

Teorema

El teorema del apretón se establece formalmente de la siguiente manera:

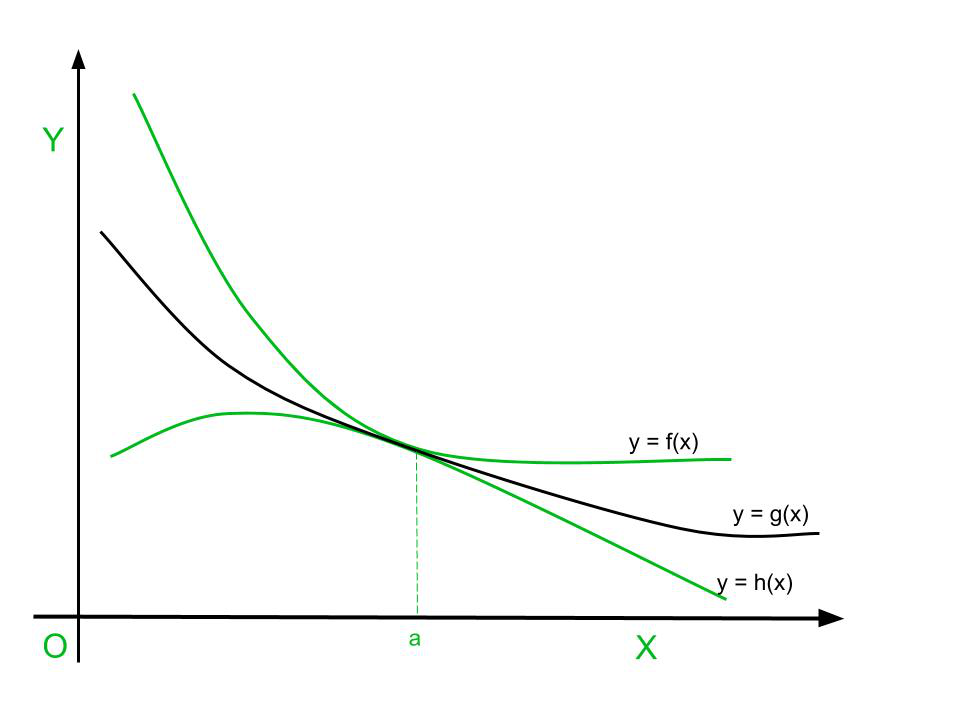
Sean funciones f(x), g(x), h(x) funciones reales tales que h(x) ≤ g(x) ≤ f(x). Entonces, para todo x en el dominio de la función,

$if\ \lim\limits_{x\rightarrow a}h(x)=\lim\limits_{x\rightarrow a}f(x)=L, then \lim\limits_{x\rightarrow a}g(x)=L$
Aquí se dice que las funciones h y f son límites inferior y superior de g respectivamente. La función anterior se representa en un gráfico a continuación.

Squeeze Theorem

Desigualdad importante

$\\cos\ x<\dfrac{\sin\ x}{x}<1,\ 0<|x|<\dfrac{\pi}{2}, \\ as\ \sin (-x)\ =\ -\sin\ x \ and\ \cos(-x)\ =\ \cos\ x, \\ so\ we\ just\ prove\ the\ inequality\ for\ the\ interval\ (0,\dfrac{\pi}{2})$
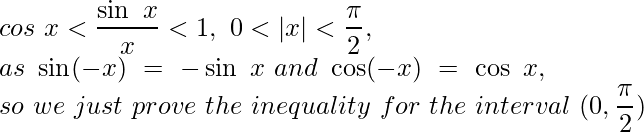
Proof:

Considere la siguiente imagen:

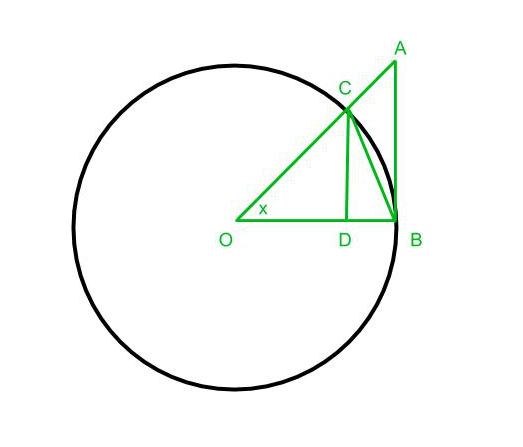
En el diagrama de arriba O es el centro del círculo AB es una tangente del círculo desde el punto B y CD es perpendicular a OB y el ángulo COD es x radianes

$here,\ Area\ of \ \triangle OBC\ < \ Area\ of\ sector\ OBC\ < Area\ of\ \triangle OBA\\\qquad\\ \implies\ \dfrac{1}{2}OB.CD<\dfrac{x}{2\pi}\pi(OB)^2<\dfrac{1}{2}OB.BA\\\qquad\\ \implies\ CD<x.(OA)<AB.\\\qquad\\ in\ \triangle OCD\\\qquad\\ \sin x=\dfrac{CD}{CO}=\dfrac{CD}{OB}(OC=OB=radius)\ hence\ CD=OB\sin x\\\qquad\\ \tan x=\dfrac{AB}{OA}\ hence\ AB=OB\tan x\\\qquad\\ \implies OB\sin x\ <\ OB.x\ <\ OB\tan x\ and OB>0\\\qquad\\ \implies \sin x\ <\ x\ <\ \tan x\\\qquad\\ 0\ <\ x\ <\ \dfrac{\pi}{2},\ so \ by \ dividing \ by \sin x\ on\ the\ above\ equation,\ we\ get\\\qquad\\ 1\ <\ \dfrac{x}{\sin x}\ <\ \dfrac{1}{\cos x}\\\qquad\\$

tomando los recíprocos obtenemos
$\cos x\ <\ \dfrac{\sin x}{x}\ <\ 1$

Límites importantes

$1.\ \lim\limits_{x\rightarrow\ 0}\dfrac{sin x}{x}=1$

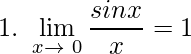
Prueba:

De la desigualdad anterior, demostramos que
$\cos x\ <\ \dfrac{\sin x}{x}\ <\ 1$
De esta ecuación, entendemos que (sen x/x) siempre se encuentra entre cos x y 1. Entonces (sen x/x) está intercalado entre 1 y cos x. Lo sabemos
$\\\qquad\\ if\ \lim\limits_{x\rightarrow a}f(x)=\lim\limits_{x\rightarrow a}h(x)=L\\\qquad\\ then \lim\limits_{x\rightarrow a}g(x)=L\\\qquad\\ \lim\limits_{x\rightarrow0}\cos\ x=1\ and\ \lim\limits_{x\rightarrow0}1=1 \\\qquad\\ \implies \lim\limits_{x\rightarrow0}\dfrac{\sin\ x}{x}=1$

$2.\ \lim\limits_{x\rightarrow 0}\dfrac{1-cosx}{x}=0$

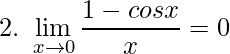
Prueba:

Para probar este límite usamos la identidad trigonométrica
$1-\cos x=2\sin^2(\dfrac{x}{2})\\\qquad\\ \implies\lim\limits_{x\rightarrow0}\dfrac{1-\cos x}{x}=\lim\limits_{x\rightarrow0}\dfrac{2\sin^2\frac{x}{2}}{x}=\lim\limits_{x\rightarrow0}\dfrac{\sin \frac{x}{2}}{\frac{x}{2}}.\sin\frac{x}{2}\\\qquad\\ =\lim\limits_{x\rightarrow0}\dfrac{sin\frac{x}{2}}{\frac{x}{2}}\lim\limits_{x\rightarrow0}\sin \dfrac{x}{2}\ =\ 1.0\ =0\\\qquad\\ \implies 1-\cos x=2\sin^2(\dfrac{x}{2})\ =\ 0$

Publicación traducida automáticamente

Artículo escrito por somsagar2019 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Teorema

Desigualdad importante

Límites importantes

Deja una respuesta Cancelar la respuesta