Teorema de conteo de órbitas o lema de Burnside

El lema de Burnside también se conoce a veces como teorema de conteo de órbitas . Es uno de los resultados de la teoría de grupos . Se utiliza para contar objetos distintos con respecto a la simetría. Básicamente nos da la fórmula para contar el número total de combinaciones, donde dos objetos que son simétricos entre sí con respecto a la rotación o reflexión se cuentan como un único representante .

Por lo tanto, Burnside Lemma’s establece que el número total de objetos distintos es: 
donde:  

• c(k) es el número de combinación que permanece sin cambios cuando se aplica la rotación K-ésima, y
• N es el número total de formas de cambiar la posición de N elementos.

Por ejemplo:
Supongamos que tenemos un collar de N piedras y podemos colorearlo con M colores. Si dos collares son similares después de la rotación, los dos collares se consideran similares y se cuentan como una combinación diferente. Ahora supongamos que tenemos N = 4 piedras con M = 3 colores, entonces

Como tenemos N piedras, por lo tanto, tenemos N variaciones posibles de cada collar por rotación: 

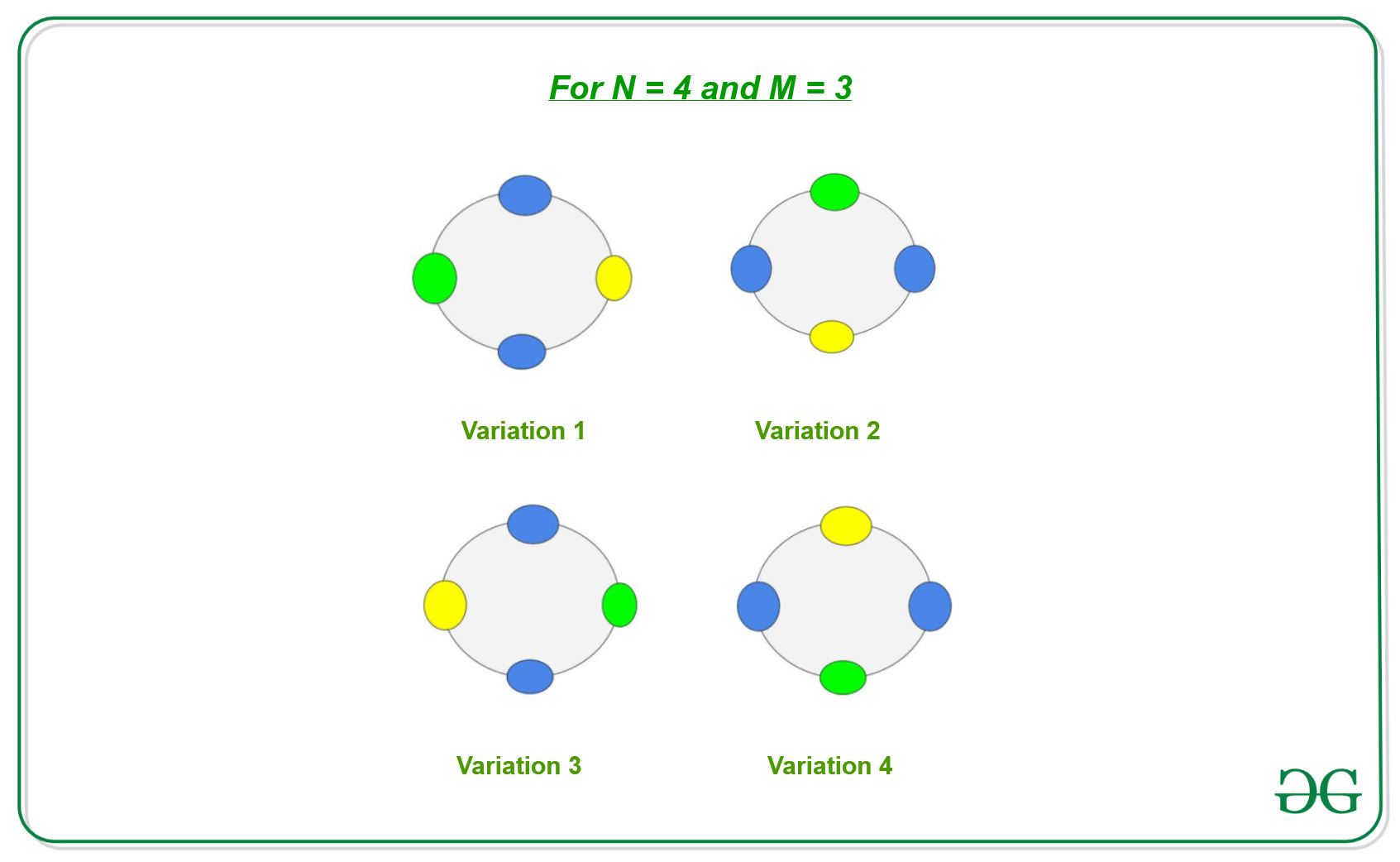
Observaciones: Hay N formas de cambiar la posición del collar ya que podemos rotarlo de 0 a N – 1 vez.

1. Hay  maneras de colorear un collar. Si el número de rotaciones es 0, entonces todas las  formas siguen siendo diferentes.
2. Si el número de rotación es 1, entonces solo hay M collares que serán diferentes en todos los  sentidos.
3. Generalmente, si el número de rotaciones es K ,  los collares seguirán siendo los mismos en todos los  sentidos.

Por lo tanto, para un número total de collares distintos de N piedras después de colorear con M colores es la suma de todos los collares distintos en cada rotación. Está dado por: 

A continuación se muestra la implementación del enfoque anterior: 

// C++ program for implementing the
// Orbit counting theorem
// or Burnside's Lemma
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to find result using
// Orbit counting theorem
// or Burnside's Lemma
void countDistinctWays(int N, int M)
{
 
    int ans = 0;
 
    // According to Burnside's Lemma
    // calculate distinct ways for each
    // rotation
    for (int i = 0; i < N; i++) {
 
        // Find GCD
        int K = __gcd(i, N);
        ans += pow(M, K);
    }
 
    // Divide By N
    ans /= N;
 
    // Print the distinct ways
    cout << ans << endl;
}
 
// Driver Code
int main()
{
 
    // N stones and M colors
    int N = 4, M = 3;
 
    // Function call
    countDistinctWays(N, M);
 
    return 0;
}

// Java program for implementing the
// Orbit counting theorem
// or Burnside's Lemma
class GFG{
 
static int gcd(int a, int b)
{
    if (a == 0)
        return b;
         
    return gcd(b % a, a);
}
 
// Function to find result using
// Orbit counting theorem
// or Burnside's Lemma
static void countDistinctWays(int N, int M)
{
    int ans = 0;
 
    // According to Burnside's Lemma
    // calculate distinct ways for each
    // rotation
    for(int i = 0; i < N; i++)
    {
        // Find GCD
        int K = gcd(i, N);
        ans += Math.pow(M, K);
    }
 
    // Divide By N
    ans /= N;
 
    // Print the distinct ways
    System.out.print(ans);
}
 
// Driver Code
public static void main(String []args)
{
     
    // N stones and M colors
    int N = 4, M = 3;
 
    // Function call
    countDistinctWays(N, M);
}
}
 
// This code is contributed by rutvik_56

// C# program for implementing the
// Orbit counting theorem
// or Burnside's Lemma
using System;
class GFG
{
static int gcd(int a, int b)
{
    if (a == 0)
        return b;       
    return gcd(b % a, a);
}
 
// Function to find result using
// Orbit counting theorem
// or Burnside's Lemma
static void countDistinctWays(int N, int M)
{
    int ans = 0;
 
    // According to Burnside's Lemma
    // calculate distinct ways for each
    // rotation
    for(int i = 0; i < N; i++)
    {
        // Find GCD
        int K = gcd(i, N);
        ans += (int)Math.Pow(M, K);
    }
 
    // Divide By N
    ans /= N;
 
    // Print the distinct ways
    Console.Write(ans);
}
 
// Driver Code
public static void Main(string []args)
{
     
    // N stones and M colors
    int N = 4, M = 3;
 
    // Function call
    countDistinctWays(N, M);
}
}
 
// This code is contributed by pratham76

<script>
 
// Javascript <script>
 
// Javascript program for implementing the
// Orbit counting theorem
// or Burnside's Lemma
 
function gcd(a, b)
{
    if (a == 0)
        return b;
          
    return gcd(b % a, a);
}
  
// Function to find result using
// Orbit counting theorem
// or Burnside's Lemma
function countDistinctWays(N, M)
{
    let ans = 0;
  
    // According to Burnside's Lemma
    // calculate distinct ways for each
    // rotation
    for(let i = 0; i < N; i++)
    {
        // Find GCD
        let K = gcd(i, N);
        ans += Math.pow(M, K);
    }
  
    // Divide By N
    ans /= N;
  
    // Print the distinct ways
    document.write(ans);
}
 
// Driver Code
     
    // N stones and M colors
    let N = 4, M = 3;
  
    // Function call
    countDistinctWays(N, M);
       
</script>

24