Declaración del teorema: El teorema de Tales o el teorema básico de proporcionalidad establece que si se dibuja una línea paralela a un lado de un triángulo que se cruza con los otros dos lados en puntos distintos, entonces los otros dos lados se dividen en la misma proporción.
Prueba del teorema básico de proporcionalidad
Supongamos que tenemos un triángulo ABC, si trazamos una línea LM paralela al lado BC entonces el teorema establece que,
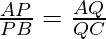
En el triángulo ABC, une el vértice B con M en la línea AC y une el vértice C en la línea AB. Luego, suelte un MX perpendicular en la línea AB y un LY perpendicular en AC. El siguiente diagrama muestra la construcción de la misma.
ya que el area del triangulo =
Área de
ALM=
Área de
Área de
Área de
Relación de área de
—-(1)
Relación de área de
—-(2)
De acuerdo con la propiedad de los triángulos, los triángulos sobre la misma base y entre las mismas líneas paralelas tienen áreas iguales.
Por lo tanto,
De las ecuaciones (1), (2) y (3) podemos concluir:
Por lo tanto, se demuestra el teorema básico de proporcionalidad.
Ejemplos resueltos sobre el teorema básico de proporcionalidad
Ejemplo 1. En un ∆ABC, los lados AB y AC son cortados por una línea en D y E respectivamente, que es paralela al lado BC. Demostrar que AD/AB = AE/AC.
Solución:
Dado: DE || ANTES DE CRISTO. Entonces, AD/DB = AE/EC
o Intercambiando las proporciones como => DB/AD = EC/AE
Ahora suma 1 en ambos lados=> (DB/AD) + 1 = (EC/AE) + 1
(DB + AD)/AD = (EC+ AE)/AE
AB/AD = AC/AE
Si volvemos a intercambiar las proporciones, obtenemos => AD/AB = AE/AC
Por lo tanto, probado.
Ejemplo 2. En el triángulo ABC, donde DE es una línea trazada desde el punto medio de AB y termina en el punto medio de AC en E. AD/DB = AE/EC y ∠ADE = ∠ACB. Luego prueba que ABC es un triángulo isósceles.
Solución:
Dado: AD/DB = AE/EC
Por el contrario del teorema básico de proporcionalidad, obtenemos => DE || antes de Cristo
Según pregunta => ∠ADE = ∠ACB
Por lo tanto,∠ABC = ∠ACB
El lado opuesto a ángulos iguales también es igual a AB = AC
Por lo tanto, ABC es un triángulo isósceles.
Publicación traducida automáticamente
Artículo escrito por nikitadabral30 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA