Teorema del círculo de Descartes con implementación

En geometría, el teorema de Descartes establece que por cada cuatro círculos tangentes entre sí , los radios de los círculos satisfacen una cierta ecuación cuadrática. Se puede construir un cuarto círculo tangente a tres círculos dados mutuamente tangentes.
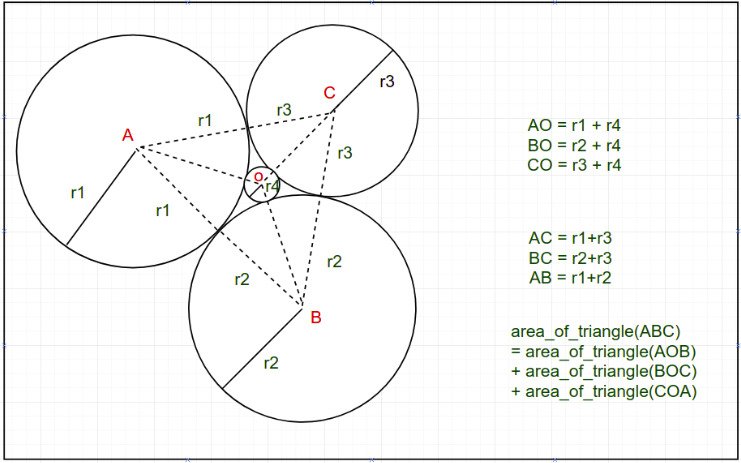
El teorema del círculo de Descartes nos ayuda a encontrar el radio de un círculo cuando hay 4 círculos con radio entero positivo r1 , r2 , r3 y r4 como se muestra en la siguiente figura. Calcula el radio r4 de la circunferencia formada por tres circunferencias de radio r1 , r2 , r3como se muestra en la imagen de abajo.
(Tenga en cuenta que los círculos en la imagen a continuación son tangentes entre sí).

Ejemplos:

Entrada: r1 = 1, r2 = 1, r3 = 1
Salida: 0,154701
Entrada: r1 =23, r2 = 46, r3 = 69
Salida: 6,000000

El teorema dice que los recíprocos de radios, o «curvaturas», de estos círculos

$k_1 = 1/r_1, k_2 = 1/r_2, k_3 = 1/r_3\:y\:k_4 = 1/r_4$
satisface la siguiente relación:
$2(k_1^2+k_2^2+k_3^2+k_4^2) = (k_1+k_2+k_3+k_4)^2$

Uno de los círculos puede encerrar a los tres restantes, como en la figura, en cuyo caso la curvatura correspondiente $(k_4 = -1/r_4)$ aquí se considera negativa y la relación anterior sigue siendo válida.
Si $k_1, k_2, k_3$ se conocen, se puede resolver para k4.
$k_4 = k_1 + k_2 + k_3 \pm 2\sqrt{k_1 k_2 + k_2 k_3 + k_1 k_3}$
Al resolver la ecuación anterior obtenemos el radio del cuarto círculo. La fórmula para encontrar el radio del cuarto círculo es:

$r_4 = (r_1*r_2*r_3)\, /\, (r_1*r_2 + r_2*r_3 + r_3*r_1 + 2.0\, *\, \sqrt{(r_1*r_2*r_3*(r_1+r_2+r_3))})$

Por lo tanto, si se conocen r1, r2 y r3, r4 se puede calcular fácilmente usando la fórmula anterior.
A continuación se muestra la implementación del enfoque anterior:

CPP

// C++ implementation of the
// above formulae
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the fourth circle's
// when three radius are given
double findRadius(double r1, double r2, double r3)
{
    double r4 = (r1 * r2 * r3)
                / (r1 * r2 + r2 * r3
                   + r1 * r3 + 2.0 * sqrt(r1 * r2 * r3 * (r1 + r2 + r3)));
 
    return r4;
}
 
// Driver code
int main()
{
    // Radius of three circles
    double r1 = 1;
    double r2 = 1;
    double r3 = 1;
 
    // Calculation of r4 using formula given above
    double r4 = findRadius(r1, r2, r3);
 
    cout << "The radius of fourth circle: " << r4;
    return 0;
}

Java

/*package whatever //do not write package name here */
// Java implementation of the
// above formulae
import java.io.*;
 
class GFG
{
   
        // Function to find the fourth circle's
        // when three radius are given
        static double findRadius(double r1, double r2, double r3)
        {
        double r4 = (r1 * r2 * r3)
                / (r1 * r2 + r2 * r3
                   + r1 * r3 + 2.0 * Math.sqrt(r1 * r2 * r3 * (r1 + r2 + r3)));
 
        return r4;
        }
   
      // Driver code
    public static void main (String[] args)
    {
       
        // Radius of three circles
    double r1 = 1;
    double r2 = 1;
    double r3 = 1;
 
    // Calculation of r4 using formula given above
    double r4 = findRadius(r1, r2, r3);
        System.out.println("The radius of fourth circle: " + r4);
    }
}
 
// This code is contributed by CoderSaty.

Python3

# Python 3 implementation of the
# above formulae
 
from math import sqrt
 
# Function to find the fourth circle's
# when three radius are given
def findRadius(r1, r2, r3):
    r4 = (r1 * r2 * r3) / (r1 * r2 + r2 * r3 + r1 * r3 + 2.0 * sqrt(r1 * r2 * r3 * (r1 + r2 + r3)))
 
    return r4
 
# Driver code
if __name__ == '__main__':
   
    # Radius of three circles
    r1 = 1
    r2 = 1
    r3 = 1
 
    # Calculation of r4 using formula given above
    r4 = findRadius(r1, r2, r3)
 
    print("The radius of fourth circle:",r4)
     
    # This code is contributed by SURENDRA_GANGWAR.

C#

// C# implementation of the
// above formulae
using System;
 
class GFG
{
 
  // Function to find the fourth circle's
  // when three radius are given
  static double findRadius(double r1, double r2, double r3)
  {
    double r4 = (r1 * r2 * r3)
      / (r1 * r2 + r2 * r3
         + r1 * r3 + 2.0 * Math.Sqrt(r1 * r2 * r3 * (r1 + r2 + r3)));
 
    return r4;
  }
 
  // Driver code
  public static void Main (String[] args)
  {
 
    // Radius of three circles
    double r1 = 1;
    double r2 = 1;
    double r3 = 1;
 
    // Calculation of r4 using formula given above
    double r4 = Math.Round(findRadius(r1, r2, r3),6);
 
    Console.Write("The radius of fourth circle: " + r4);
  }
}
 
// This code is contributed by shivanisinghss2110

Javascript

<script>
// Javascript implementation of the
// above formulae
 
// Function to find the fourth circle's
// when three radius are given
function findRadius(r1, r2, r3) {
  let r4 =
    (r1 * r2 * r3) /
    (r1 * r2 +
      r2 * r3 +
      r1 * r3 +
      2.0 * Math.sqrt(r1 * r2 * r3 * (r1 + r2 + r3)));
 
  return r4.toFixed(6);
}
 
// Driver code
 
// Radius of three circles
let r1 = 1;
let r2 = 1;
let r3 = 1;
 
// Calculation of r4 using formula given above
let r4 = findRadius(r1, r2, r3);
 
document.write("The radius of fourth circle: " + r4);
 
// This code is contributed by gfgking.
</script>

Producción:

The radius of fourth circle: 0.154701

Publicación traducida automáticamente

Artículo escrito por saintpopo y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

CPP

Java

Python3

C#

Javascript

Deja una respuesta Cancelar la respuesta