El círculo es una colección de puntos que están a una distancia fija de un punto en particular. El punto fijo se llama centro del círculo y la distancia fija se llama radio del círculo. Nos encontramos con muchos objetos en la vida real que tienen forma redonda. Por ejemplo, ruedas de vehículos, brazaletes, diales de teléfono, etc. En el reloj también, sus manecillas se mueven en forma redonda repetidamente. El camino trazado por la punta de las manecillas del reloj se llama círculo.
Veamos brevemente alguna terminología relacionada con un círculo:
- Arco: Una parte de un círculo entre dos puntos se llama arco.
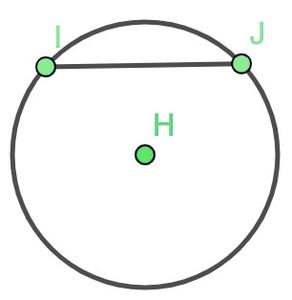
- Cuerda: si toma dos puntos I y J en un círculo, entonces el segmento de línea IJ se llama cuerda del círculo.
- Circunferencia: La longitud del círculo completo se llama su circunferencia.
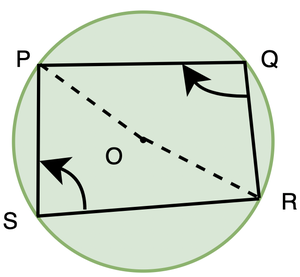
- Segmento: La región entre una cuerda y cualquiera de sus arcos se llama segmento de la región circular o simplemente segmento del círculo.
Ángulo subtendido por una cuerda en un punto
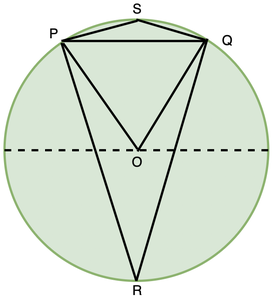
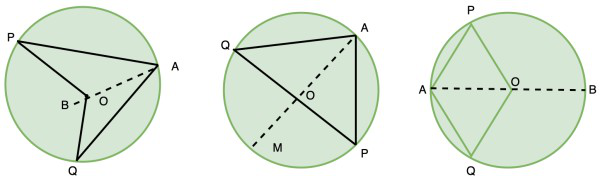
Tome un acorde en la figura de arriba PQ. R y S son dos puntos en el círculo. ∠PRQ se llama ángulo subtendido por la cuerda PQ en el punto R. De manera similar, la cuerda subtiende ángulos en S y también en el centro del círculo O. Estudiemos las relaciones entre los ángulos subtendidos por la cuerda PQ en estos puntos.
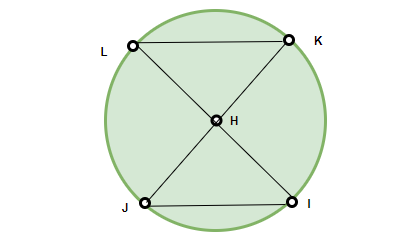
Teorema 1: Las cuerdas iguales de un círculo subtienden ángulos iguales en el centro.
Prueba:
Nos dan dos acordes KL y JI. Necesitamos probar que ∠KHL = ∠JHI.
En los triángulos KHL y JHI,
HL = HJ
Hola = Hong Kong
y se nos da que KL = JI.
Entonces, ambos triángulos son congruentes. Por lo tanto, ambos ángulos son iguales. Por lo tanto, probado.
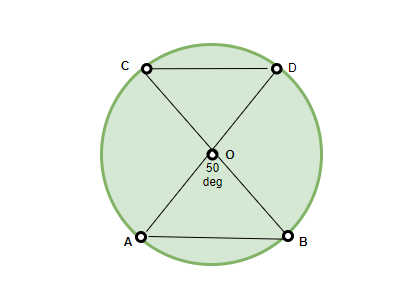
Pregunta: Si ∠AOB = 50° en la siguiente figura, ¿cuál será el ángulo subtendido por ∠COD, siempre que las cuerdas AB y CD sean iguales?
Responder:
Según el teorema mencionado anteriormente, los ángulos ∠AOB y ∠COD son iguales, ya que son cuerdas iguales que subtienden ángulos iguales en el centro. Por lo tanto, ∠COD = 50°.
Nota: El inverso de este teorema » Si los ángulos subtendidos por dos cuerdas en el centro son iguales, entonces las dos cuerdas son iguales » también es cierto y puede demostrarse de manera similar mediante las propiedades de los triángulos.
Perpendicular del centro a una cuerda
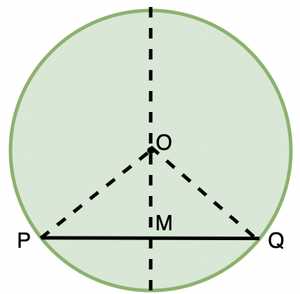
Teorema: La línea trazada por el centro de un círculo para bisecar una cuerda es perpendicular a la cuerda
Prueba:
Sea PQ la cuerda de un círculo y OM la línea desde el centro que biseca la cuerda. Aquí, M es el punto medio de la cuerda y tenemos que demostrar que ∠OMQ = 90°.
En los triángulos ΔOPM y ΔOQM.
PM = MQ (perpendicular biseca la cuerda)
OP = OQ (radio del círculo)
OM = OM (lado común de ambos triángulos)
Entonces, estos dos triángulos son congruentes. Esto da, ángulos ∠OMQ y ∠OMP como 90°
Nota: El inverso de este teorema » La perpendicular desde el centro de un círculo a una cuerda biseca la cuerda » también es cierto.
Ángulo subtendido por un arco de círculo
Si dos cuerdas de un círculo son iguales, entonces sus correspondientes arcos son congruentes y, a la inversa, si dos arcos son congruentes, entonces sus correspondientes cuerdas son iguales.
Similar al caso de las cuerdas, los arcos iguales también subtienden ángulos iguales en el centro.
Teorema: El ángulo subtendido por un arco en el centro es el doble del ángulo subtendido por él en cualquier punto de la parte restante del círculo.
Prueba:
Consideremos tres casos,
- Arco PQ es arco mayor.
- El arco PQ es un arco menor.
- Arco PQ es semicírculo.
Unamos AO y extendámoslo a B.
En los tres casos, ∠BOQ = ∠OAQ + ∠OQA. (El ángulo exterior de un triángulo es igual a la suma de los dos ángulos interiores opuestos).
También en el triángulo ΔOAQ,
OA = OQ (Radios del Círculo)
Por lo tanto, ∠ OAQ = ∠ OQA
esto da, ∠ BOQ = 2∠OAQ
∠ BP = 2∠OAP
de (1) y (2), ∠ BOP + ∠ BOQ = 2(∠ OAP + ∠ OAQ)
∠POQ = 2 ∠PAQ
Para el caso (iii), donde PQ es el arco mayor, (3) se reemplaza por
Ángulo de reflejo POQ = 2∠PAQ
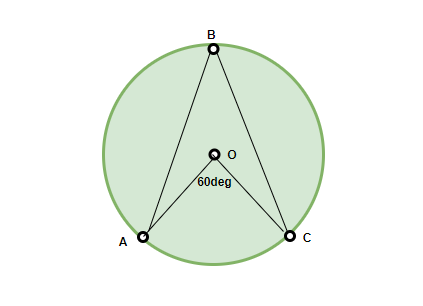
Pregunta: ¿Cuál es el valor de ∠ABC?
Responder:
Según el teorema, ∠AOC = 2 ∠ABC
Por lo tanto, ∠ABC = 60°/2 = 30°
Algunas otras propiedades:
- Los ángulos en el mismo segmento de un círculo son iguales.
- Si un segmento de línea que une dos puntos subtiende ángulos iguales en otros dos puntos que se encuentran en el mismo lado de la línea que contiene el segmento de línea, los cuatro puntos se encuentran en un círculo (es decir, son concíclicos).
Cuadriláteros cíclicos
Un cuadrilátero se llama cíclico si sus cuatro vértices se encuentran en un círculo.
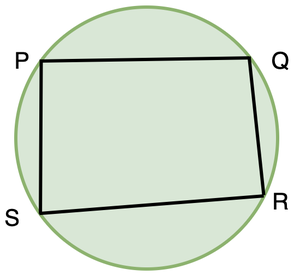
También se les llama cuadriláteros inscritos.
Teorema: La suma de cualquier par de ángulos opuestos de un cuadrilátero cíclico es 180º.
Prueba:
Considerando el arco PQR, ∠POR = 2 ∠PSR,
De manera similar, considerando PSR, reflejo ∠POR = 2∠PQR
Sabemos, ∠POR + reflejo ∠POR = 360°.
⇒ 2 ∠PSR + 2∠PQR = 360°
⇒ 2(∠PSR + ∠PQR) = 360°
⇒ ∠PSR + ∠PQR = 180°
Por lo tanto, la suma de los ángulos opuestos del cuadrilátero cíclico es 180°.
Pregunta: En la siguiente figura, BC es el diámetro del círculo, ED es una cuerda igual al radio del círculo. BE y CD cuando se extienden se intersecan en un punto F. Demuestra que ∠BFC = 60°.
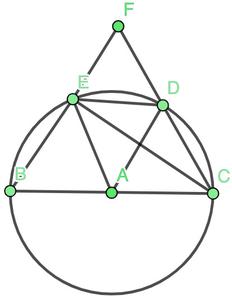
Solución:
En la figura, unir AE, AD y EC. El triángulo AED es un triángulo equilátero.
Por lo tanto, ∠EAD = 60 o . Ahora, ∠ECD se convierte en 30 o .
Sabemos que ∠BEC = 90 o .
Entonces, por la propiedad de los ángulos exteriores del triángulo,
∠BEC = ∠ECD + ∠BFC,
90 o = 30 o + ∠BFC
⇒60 o = ∠BFC
Por lo tanto, Probado.
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA